Figure 10-74 is an overhead view of a rod of length d and negligible mass that rotates at angular speed ω in the horizontal plane about a vertical axis through point O. Particle A of mass m is attached at the center point and an identical particle B is attached at the far end. Find the angular momentum of particle B with respect to particle A.
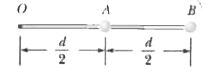
mωd24
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
43 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
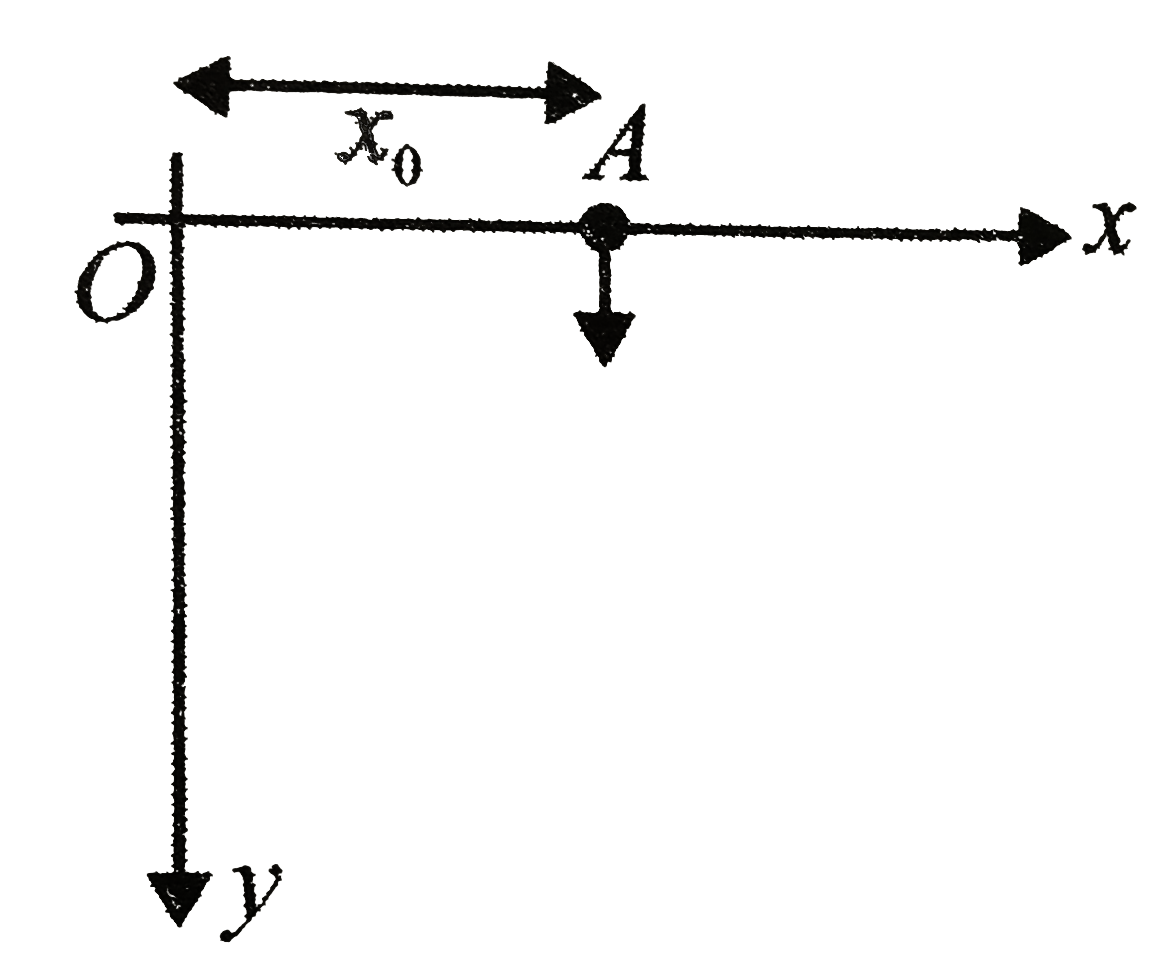
A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution
Knowledge Check
A uniform disc of radius 'a' and mass 'm' is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is
Aω/√3Bω/3Cω/√4Dω/5A uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
Aω6Bω3Cω2Dω5A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AY
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
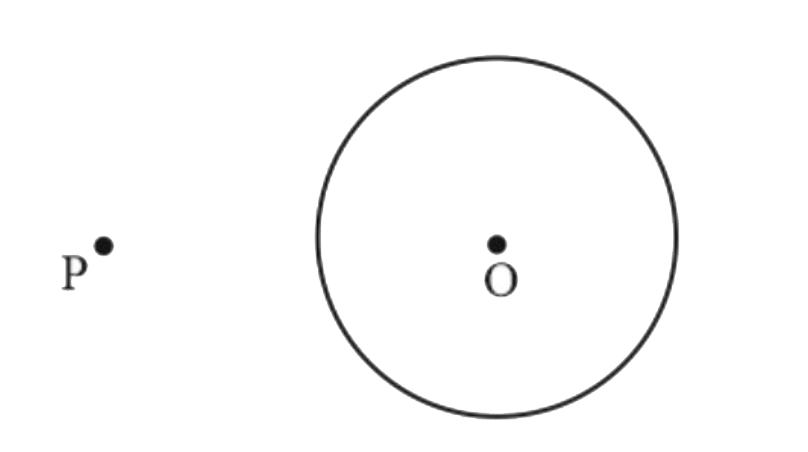
View SolutionConsider a particle , moving in a circle with constant speed . P is a point outside the circle , in the same plane . Then , the angular momentum of the particle about the point P is
View SolutionA particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

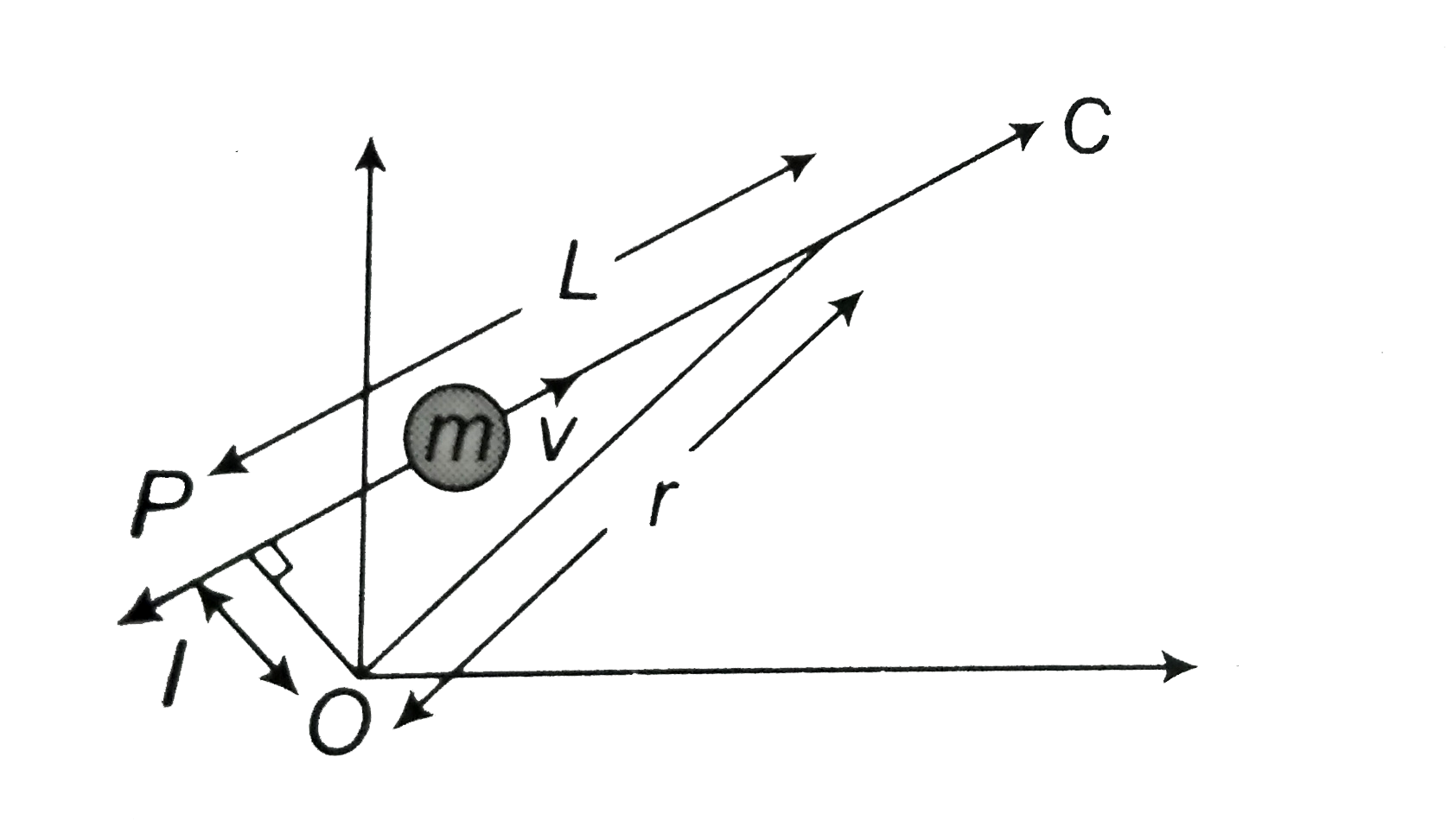
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
View Solution
