From a uniform circular disc of diameter d,a circular disc of diameter d/6 and having centre at a distance d/4 from the centre of the disc is scooped out. Determine the centre of mass of remaining portion.
Let m be the mass per unit area of the disc.

∴ Mass of disc M=m×πD24
It is concentrated at the centre O of the disc, Fig.
Mass of cut off portion,
m1=m×π(D/6)24=mπD2144=M36
It is concentrated at O1 , where OO1=D/4.
Let the centre of mass of remaining portion of disc be at O2 where OO2=x
Mass of remaining portion of disc
m2=m×πD24−mπD2144=35M36
Clearly, m1×D4=m2x
x=m1m2D4
x=M/3635M/36×D4=D35×4=D140
∴ Centre of mass of remaining portion of disc is at D/140 from centre O of the disc, to the left side.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE B2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE C2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE A2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
From a uniform circular disc of diameter D, a circular disc or hole of diameter D/6 and having its centre at a distance of D/4 from the centre of the disc is scopped out. Determine the centre of mass of the remaining portion.
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2) - Question 2 - Select One
A circular plate of uniform thickness has a diameter of 28cm. A circular portion of diameter 21cm is removed from the plate as shown. Ois the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from 'O' by
 A5cmB9cmC4.5cmD5.5cm
A5cmB9cmC4.5cmD5.5cm
A circular disc of radius R4 is cut from a uniform circular disc of radius R.
The centre of cut portion is at a distance of R2 from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionFind the centre of mass of the shaded portion of a disc
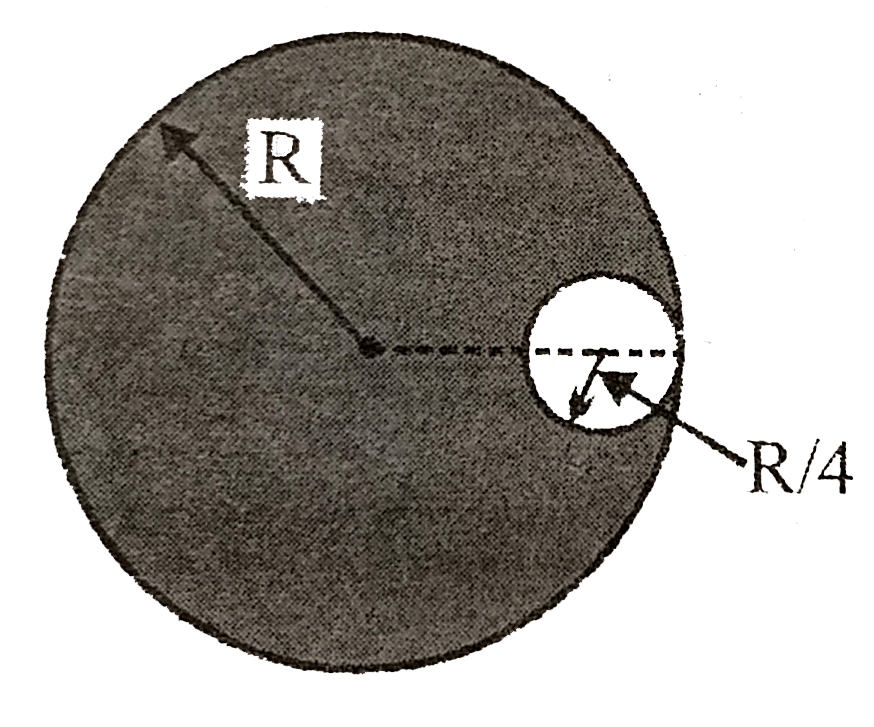 View Solution
View SolutionFind the centre of mass of the shaded portion of a disc.
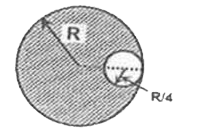 View Solution
View SolutionA uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.
 View Solution
View Solution

