Find the centre of mass of the shaded portion of a disc

Text Solution

Verified by Experts

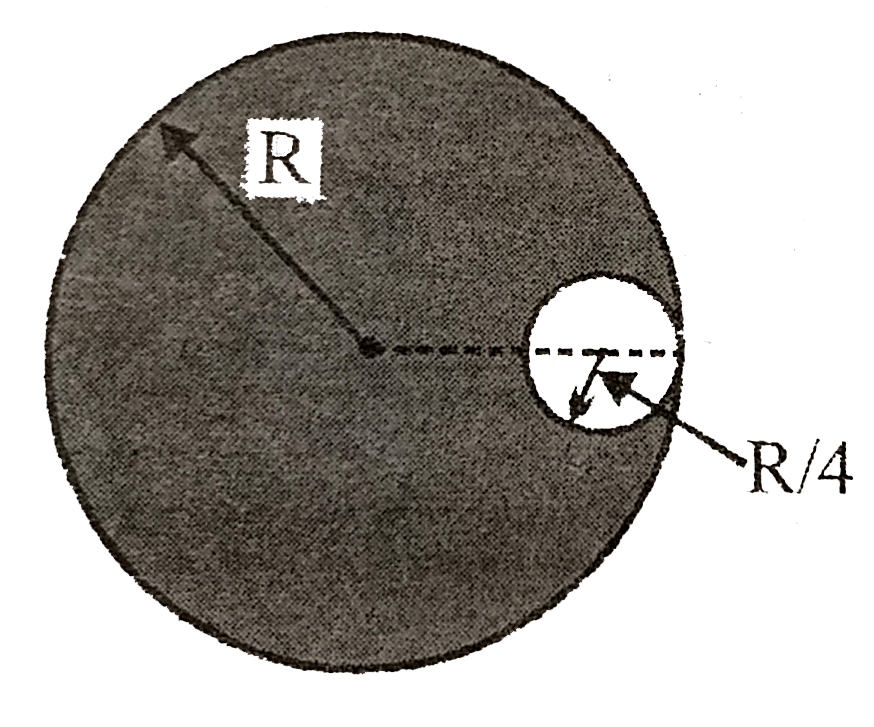
The correct Answer is: $\frac{R}{20}$ the left of disc

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

BOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]
23videos
CENTRE OF MASS & MOMENTUM CONSERVATION
BOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-2 [PARAGRAPH TYPE]
10videos
CENTRE OF MASS & MOMENTUM CONSERVATION
BOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Solved Examples
15videos
CENTRE OF MASS & MOMENTUM CONSERVATION
BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6videos
GRAVITATION

Similar Questions

Knowledge Check

Question 1 - Select One
The centre of mass of the shaded portion of the disc is: ( The mass is uniformly distributed in the shaded portion).

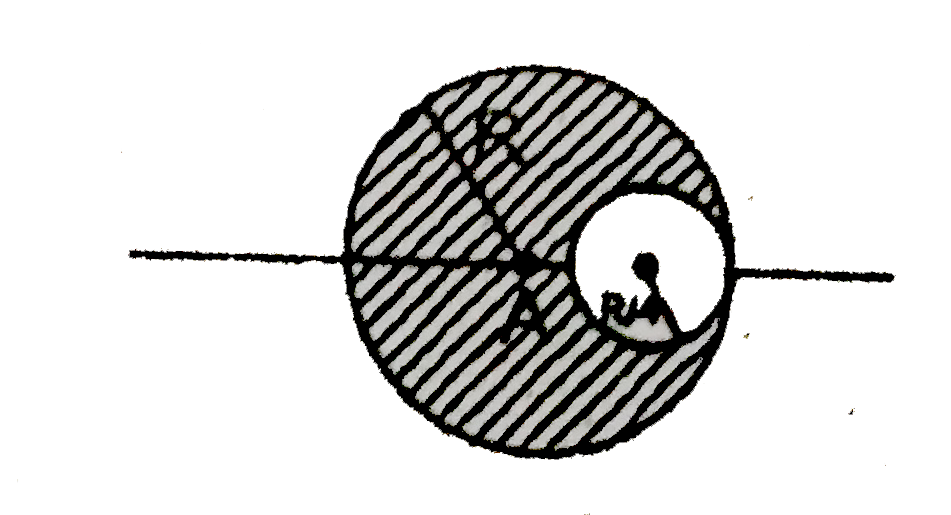A $\frac{R}{20}$ to the left of A
B $\frac{R}{12}$ to the left of A
C $\frac{R}{20}$ to the right of A
D $\frac{R}{12}$ to the right of A
Question 2 - Select One
Find the perimeter and area of the shaded portion of the adjoining diagram:

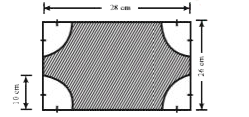A $90.8 c m, 414 c m^{2}$
B $181.6 c m, 423.7 c m^{2}$
C $90.8 c m, 827.4 c m^{2}$
D $181.6 c m, 827.4 c m^{2}$

BANSAL-CENTRE OF MASS & MOMENTUM CONSERVATION-Practice Exercise

Home
Ask Doubt
Profile