A light ray enters into a medium whose refractive index varies along the x-axis as n(x)=n0√1+x4 where n0=1. The medium is bounded by the plates x=0,x=1 & y=0. It the ray enters at the origin at an angle 30∘ with x-axis

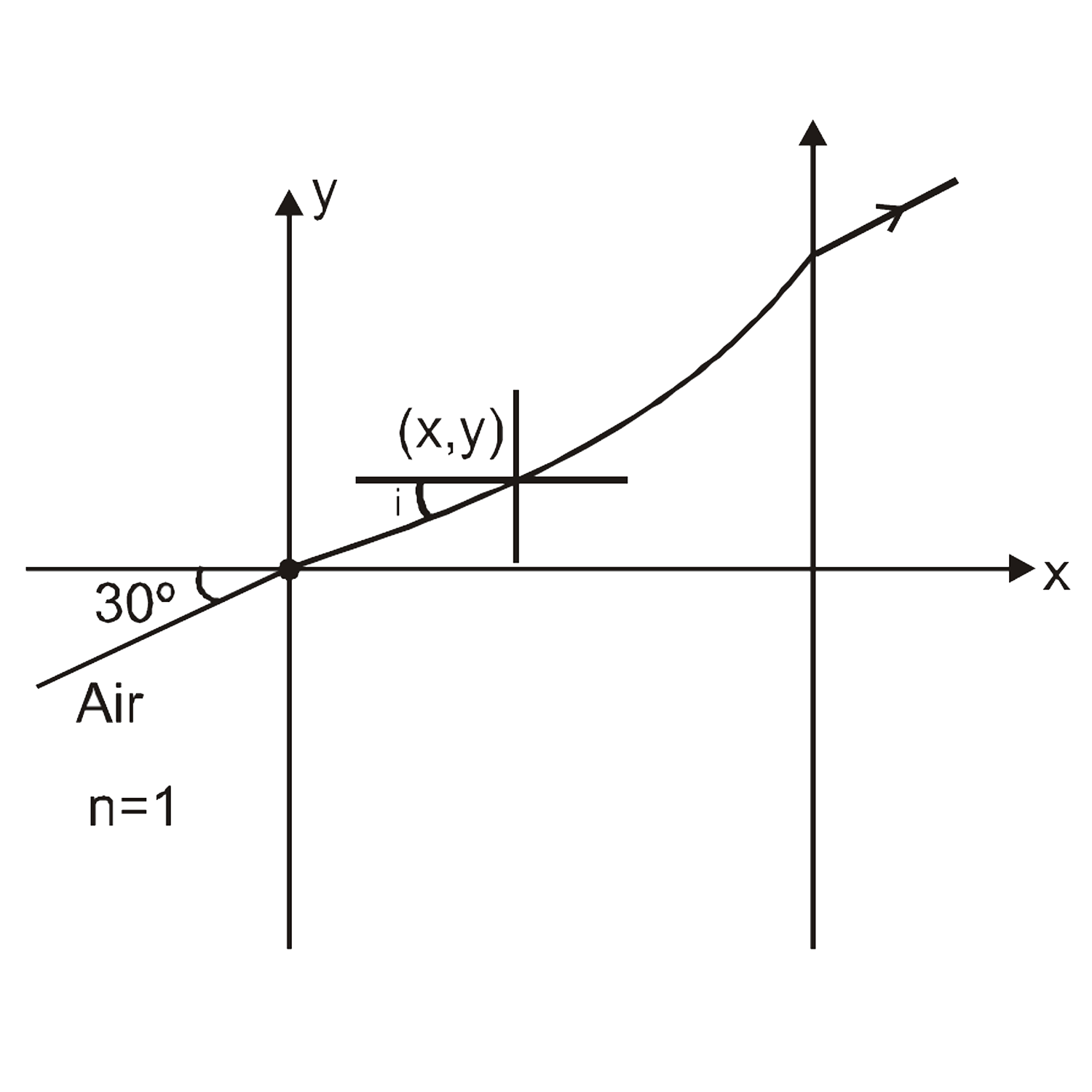
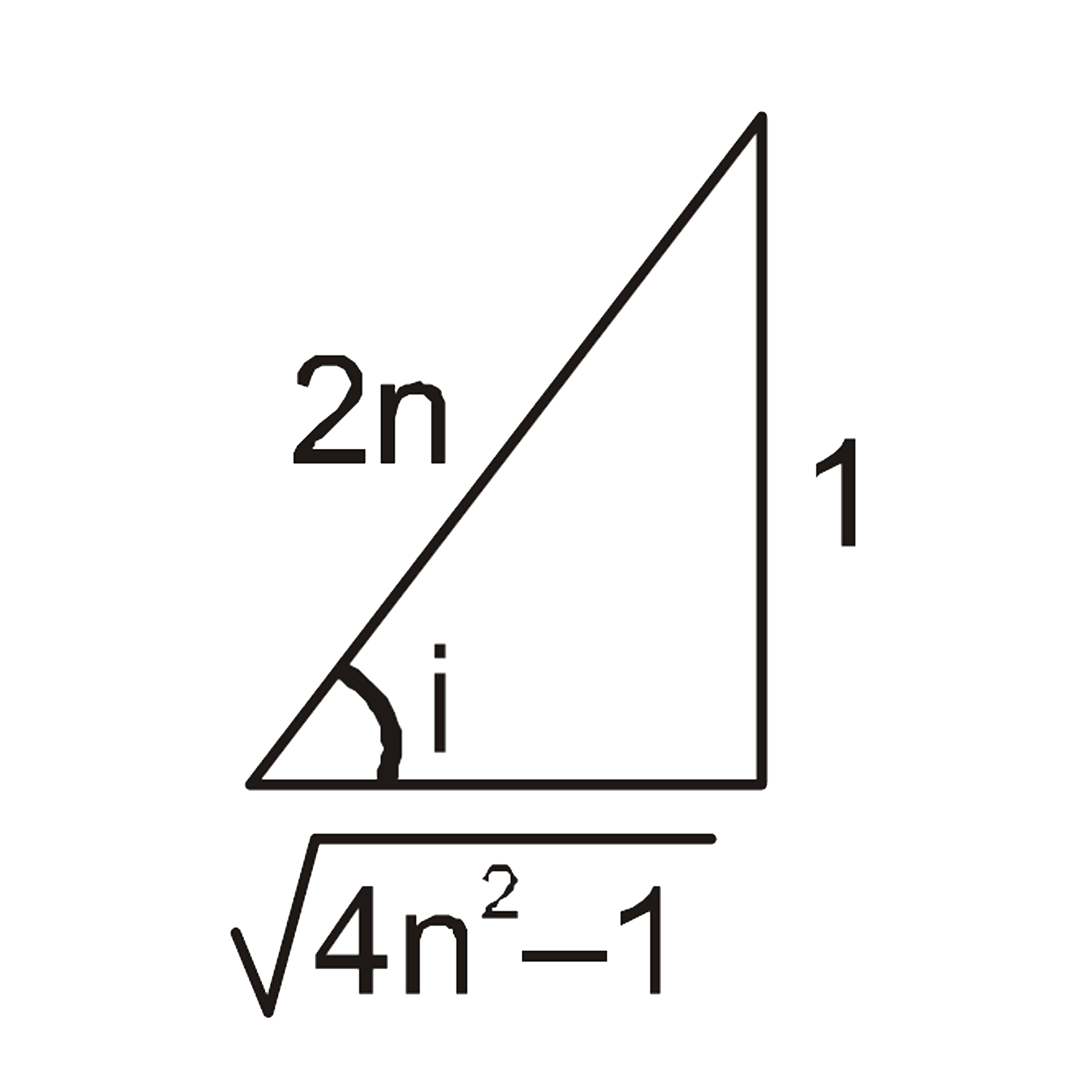
(a). 1×sin30∘=nsini
sini=12n
tani=1√4n2−1
dydx=1√x+3
∫y0dy=∫x0(x+3)−1/2dx
y=2(√1+3−√3) y=2(2−√3)
∴ position at which ray comes out of the medium is (1,2(2−√3))
Topper's Solved these Questions
Similar Questions
Knowledge Check
The area bounded by the lines x=0,y=0,x+y=1,2x+3y=6 (in square units ) is
A2B213C212D3A system of coordinatees is drawn in a medium whose refractive index vaires as μ=21+Y2 where 0≤y≤1. A ray of light is incident at origin at an angle 60∘ with y-axis as shown in figure. At point P, the ray becomes parallel to x-axis, the volue of H is -
 A{(2√3−1)}1/2B{2√3}1/2C{(√3−1)}1/2D{√(3)+1}1/2
A{(2√3−1)}1/2B{2√3}1/2C{(√3−1)}1/2D{√(3)+1}1/2A ray of light passes from vaccume into a medium of refractive index n. if the angle of incidence is twice the angle of refraction, then the angle of incidence is
Acos−1(n/2)Bsin−1(n/2)C2cos−1(n/2)D2sin−1(n/2)
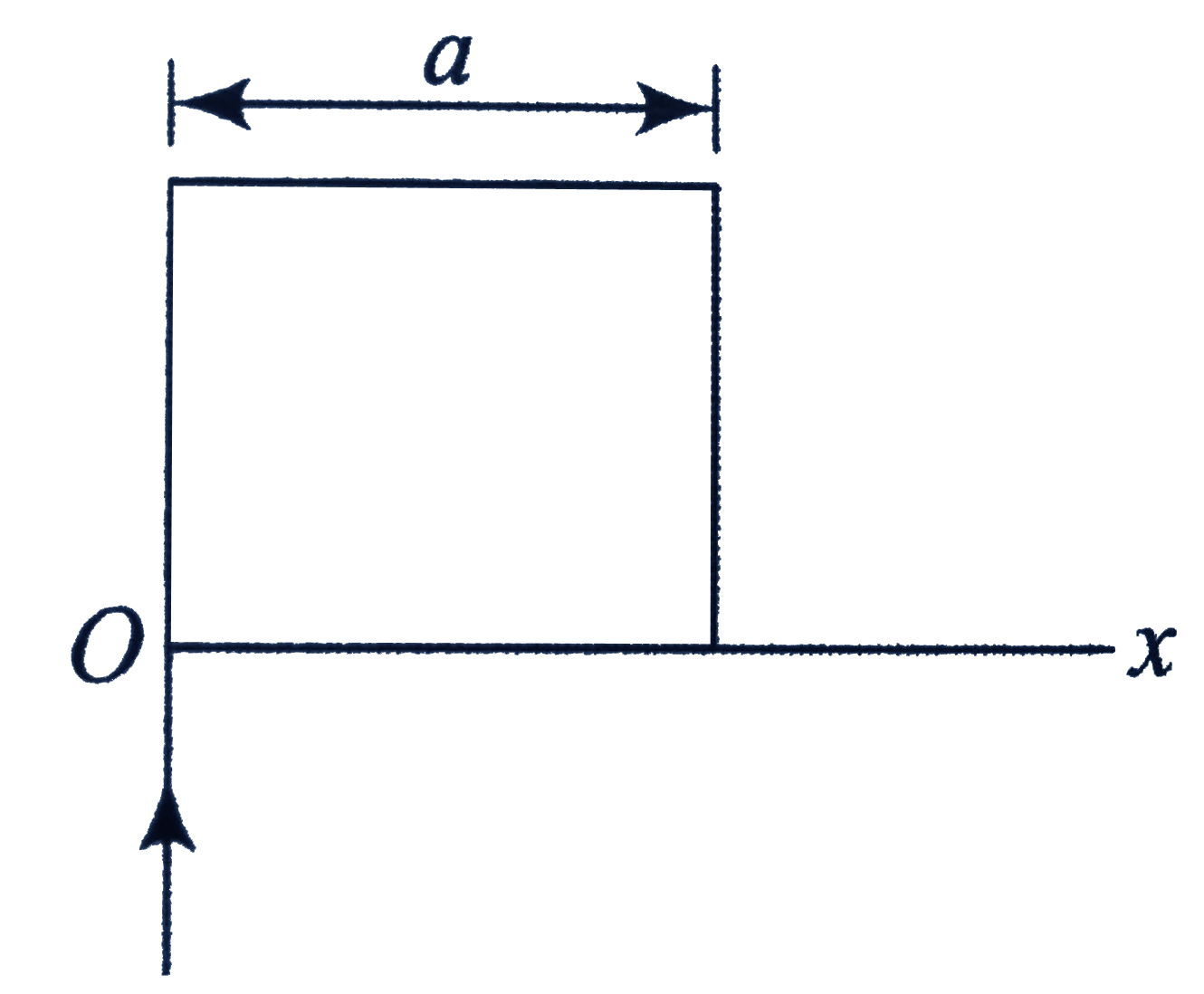
The refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View SolutionThe area bounded by the parabola y=√6x+4, X - axis from x = 0 to x = 2 is
View SolutionLight of wavelength λ0 in air enters a medium of refractive index n. If two points A and B in this medium lie along the path of this light at a distance x, then phase difference ϕ0 between these two point is
View SolutionA ray of light, travelling in a medium of refractive index mu, is incident at an angle i on a composite transparent plate consisting of three plates of refractive indices μ1,μ2andμ3. The ray emerges from the composite plate into a medium of refractive index μ4, at angle x. Then,
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View Solution
