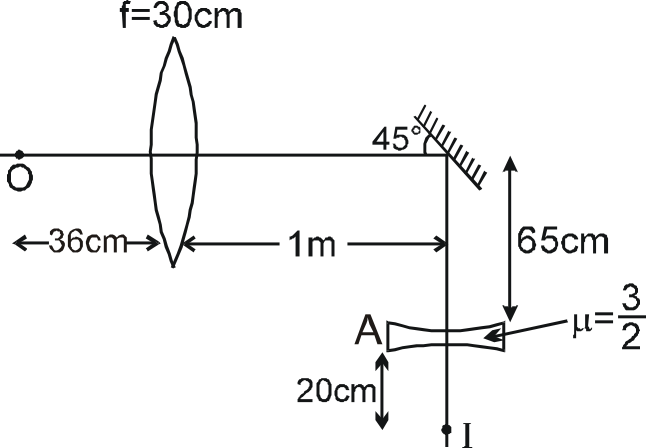
The final image  of the object O shown in the figure is formed at point 20 cm below a thin equi-concave lens, which is at a depth of 65 cm from principal axis. From the given geometry, calculate the radius of curvature in cm of lens kept at "A". (Refractive index of equi-convex lens is 1.5 and placed in air.

Video Solution

Text Solution

Verified by Experts

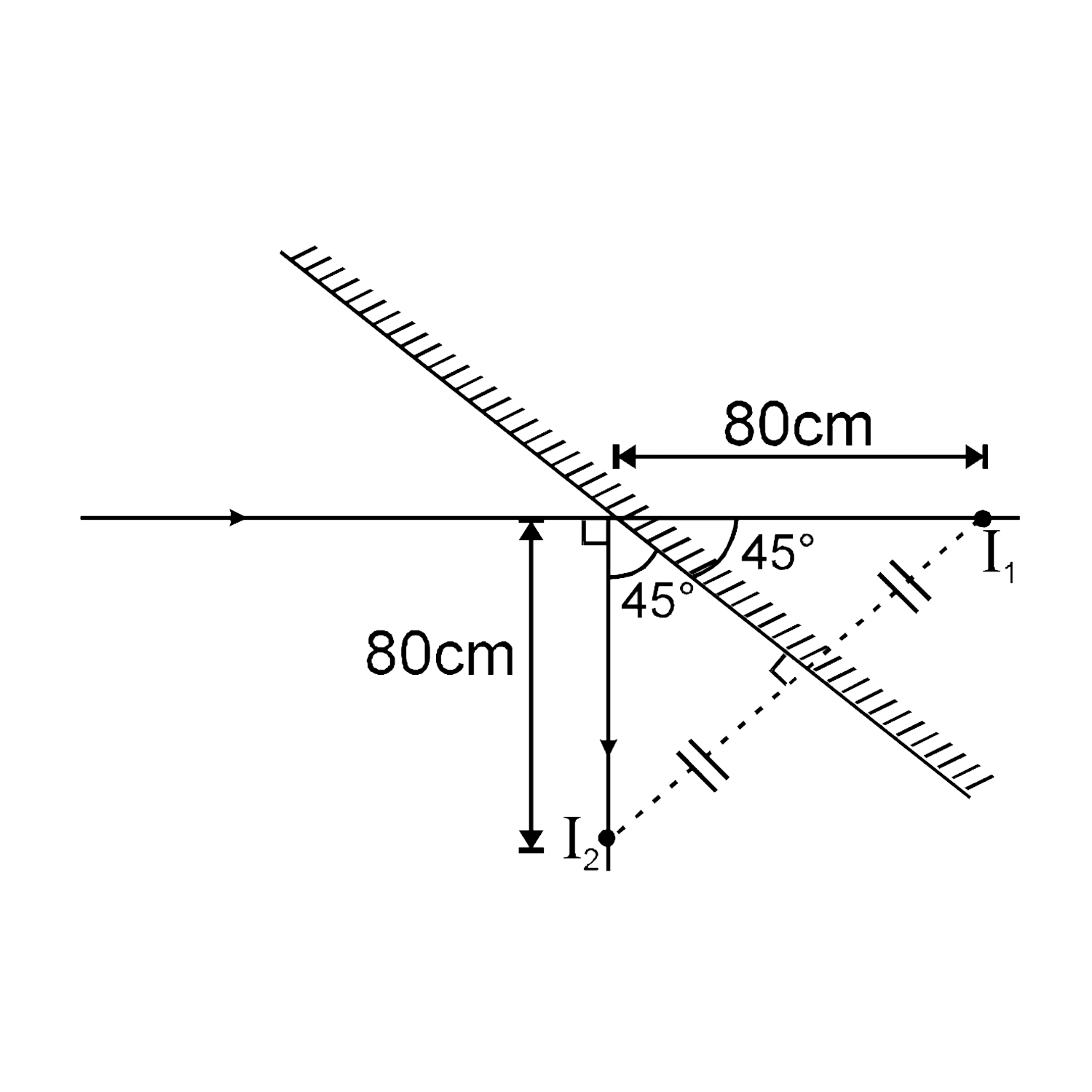
Image formation due to convex lens
$\frac{1}{v} - \frac{1}{- 36} = \frac{1}{30} \Rightarrow v = \frac{30 \times 36}{6} = 180 c m$
This image will act like a virtual object for mirror and after reflection from mirror its image (shown by $I_{2}$ ) will be formed at 80 cm below optical axis of convex lens. ltbr> For concave lens, this image will be object at a position of 15 cm below the lens for final image formed by concave lens
$\frac{1}{20} - \frac{1}{15} = \frac{1}{f} \frac{1}{f} = - \frac{5}{300}$
Also
$\frac{1}{f} = (μ - 1) (- \frac{1}{R} - \frac{1}{R})$
or $- \frac{5}{300} = (\frac{3}{2} - 1) (- \frac{2}{R}) \Rightarrow R = \frac{300}{5}$

Updated on:21/07/2023

The power in dioptre of an equi-convex lens with radii of curvature of 10cm and refractive index 1.6 is
A $+ 12$
B $+ 18$
C $+ 1.2$
D $+ 1.8$
The size of the image of an object,which is at infinity, as formed by a convex lens of focal length $20$ cm is placed between the convex lens and the image at the distance of $26$ cm from the convex lens, the new size of the image is
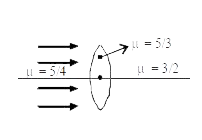
A $1.25$ cm
B $2.5$ cm
C $1.05$ cm
D $2$ cm
A bi-convex lens is formed with two thin plano-convex lenses as shown in the figure. Refractive index n of the first lens is 1.5 and that of the second lens is 1.2. Both the curved surface are of the same radius of curvature R=14 cm. For this bi-convex lens, for an object distance of 40 cm, the image distance will be

A $- 280.0 c m$
B40.0 cm
C21.5 cm
D13.3 cm