A tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
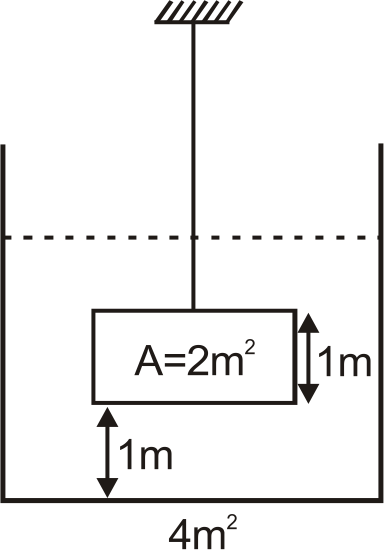
The downwards force exerted by the water on the top surface of the object is
2.0×105N
2.1×105N
2.2×105N
2.3×105N
(i) By conservation of volume
4xh=4x2+2x1=10
h=2.5 m
Pressure at top of the object
=P0+0.5×1000×10
=1.05x 105N/m2
F=P1A
=1.05×105×2=2.1×105N
By F.B.D. T+P2A=mg=P1A
T=mg+(P2+P1)A
=mg−(P2−P1)A
=2×2000×10−(.2×15N
=.4×105−0.2×105=0.2×105N
Fb=V.ρwg
=2×1000×10=0.2×105N
It is also equal to net contact force by the liquid =P2A−P1A
=0.2×105N
Note: Net contact force and buyont force are same.

Topper's Solved these Questions
Similar Questions
A tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
View SolutionA rigid cylindrical container having a cross sectional area of 0.2m2 is filled with water up to a height of 5.0m. There is a piston of negligible mass over the water. Piston can slide inside the container without friction. When a weight of 2000kg is placed over the piston, it moves down by 0.25 mm compressing the water.
ρ= Density of water =103kg/m2,Patm= Atmospheric pressure =105N/m2 and g=10m/s2. With this information calculate the speed of sound in water.

View Solution
Knowledge Check
A tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
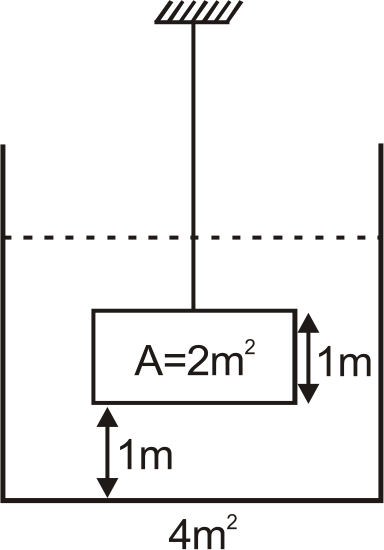
The buyont force on the object isA0.1×105NB0.2×105NC0.3×105ND0.4×105NA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
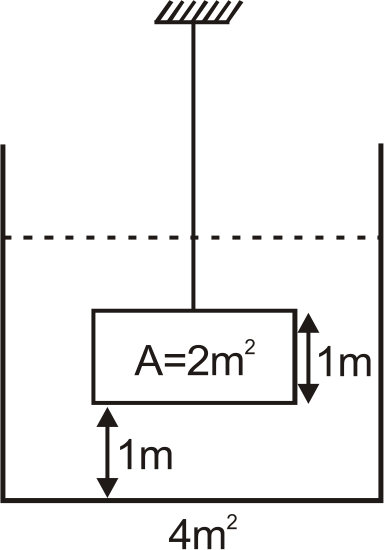
The tension in the wire isA0.1×105NB0.2×105NC0.3×105ND0.4×105NA tank of large base area is filled with water up to a height of 5m. A hole of 2cm2 cross section in the bottom allows the water to drain out in continuous streams. For this situation, mark out the correct statement(s) (take ρwater=1000kg/m3,g=10ms−12)
 AThe cross-sectional area of the emerging stream of water decreases as it falls down.BThe cross-sectional area of the emerging stream of water increases as it falls down.CAt a distance of 5m below the bottom of the tank, the cross-sectional area of the stream is 1.414cm2.DAt a distance of 5m below the bottom of the tank, the cross-sectional area of the stream is 2.86cm2.
AThe cross-sectional area of the emerging stream of water decreases as it falls down.BThe cross-sectional area of the emerging stream of water increases as it falls down.CAt a distance of 5m below the bottom of the tank, the cross-sectional area of the stream is 1.414cm2.DAt a distance of 5m below the bottom of the tank, the cross-sectional area of the stream is 2.86cm2.
Water is filled in a tank upto a height of 2m .A wooden cylinder of weight 10kg is floating on the surface of water partially immersed.If cross sectional area of tank is 1m2 and that of cylinder is 0.5m2, then the total pressure (in Pa) at the bottom of tank is (Po=atmospheric pressure )
View SolutionCalculate the water pressure and the thrust at the bottom of a tank whose length width and the depth are 2m, 1.5 m and 1m respectively. Density of water is 1000kgm−3
View SolutionIf the pressure at half the depth of a tank is equal to 23 the pressure at the bottom of the tank, then the height of the water column in the tank is
(Atmospheric pressure =105N/m2)
View SolutionA glass of water upto a height of 10 cm has a bottom of area 10cm2 , top of area 30cm2 and volume 1 litre. The downward force exerted by water on the bottom is…(Taking g=10m/s2 ,density of water =103kg/m3 , atmosphereic pressure =1.01×105N/m2)
View SolutionA tank of height 5 m/s completely filled with water. There is a hole of cross sectional area 1cm2 near its bottom. What is the initial volume of water that will come out of the hole per second. (Use g=10m/s2)
View Solution