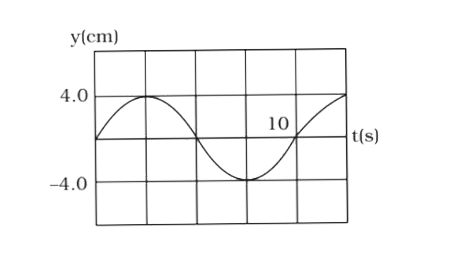
For a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
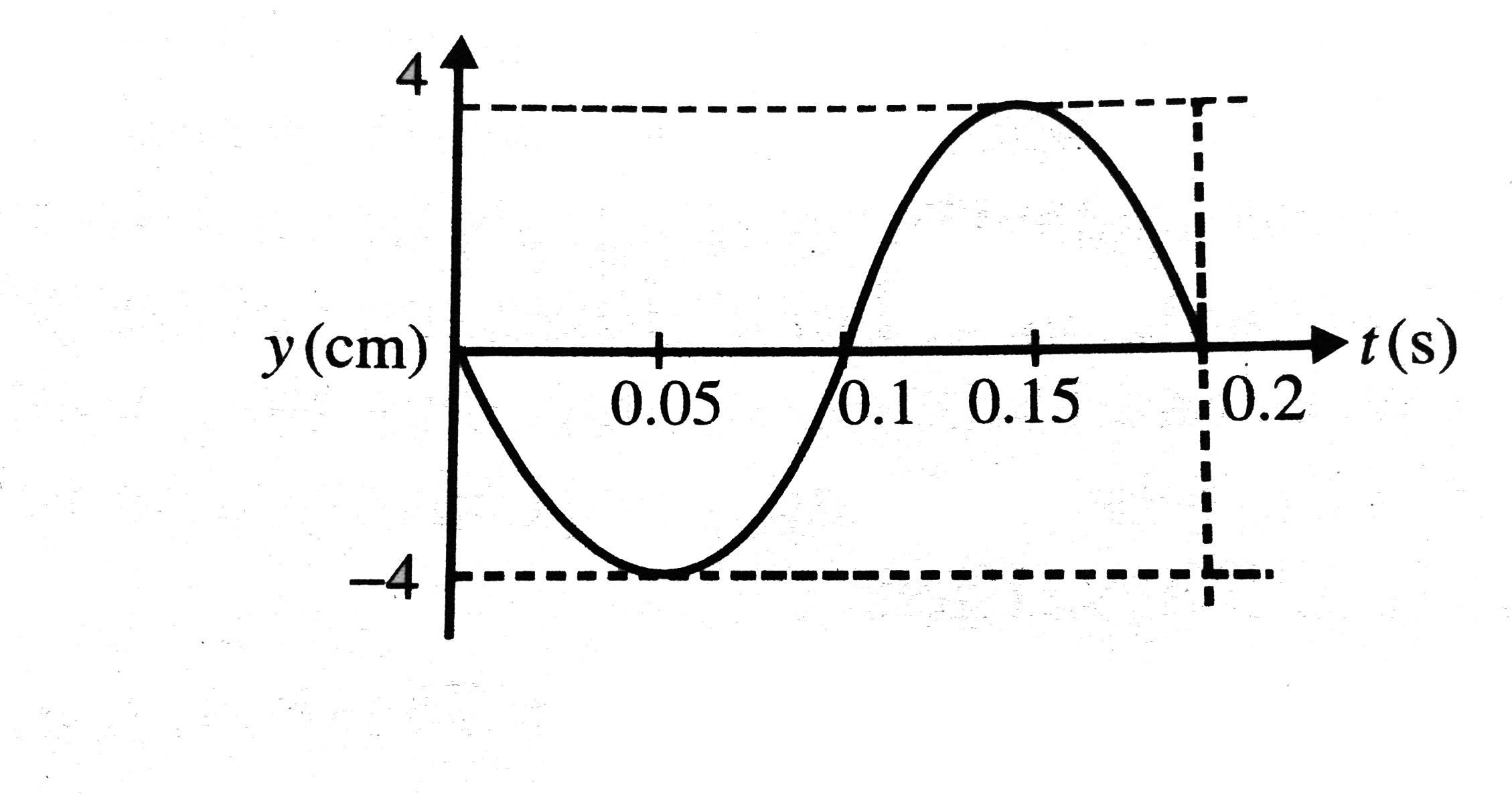
Transverse displacement of the particle at x=0.05 m and t=0.05 s is −2√2 cm
Transverse displacement of the particle at x=0.04 m and t=0.025 s is −2√2 cm
Speed of the travelling waves that interface to produce this standing wave is 2 m/s
The transverse velocity of the string particle at x=115 m and t=0.1 s is 20π cm/s
λ4=0.1⇒λ=0.4m
from graph ⇒ T=0.2 sec and amplitude of standing wave is 2A=4cm
Equation of the standing wave
y(x,t)=−2Acos(2π0.4x)sin(2π0.2t) cm
y(x=0.05,t=0.05=−2√2 cm
y(x=0.05,t=0.25=−2√2cos36∘
speed =λT=2m/sec
Vy=dydt=−2A×2π0.2cos(2πx0.4)cos(2πt0.2)
Vy=(x=115m,t=0.1)=20π cm/sec.
Topper's Solved these Questions
Similar Questions
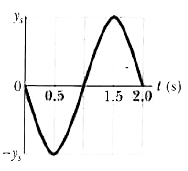
For a particular transverse standing wave on a long string, one of the antinodes is at r=0 and an adjacent node is at x=0.10 m. The displacement y(t) of the string particle at x =0 is shown in Fig. 16-40, where the scale of the y axis is set by ys=4.0cm. When t = 0.50 s, what is the displacement of the string particle at (a) x= 0.20 m and (b) x= 0.30 m? What is the transverse velocity of the string particle at x =0.20 m at (c) t=0.50s and (d) t=1.0s? (e) Sketch the standing wave at t=0.50s for the range x=0 to x=0.40m.
 View Solution
View Solution(i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x=0 and x=1m are given by y(0,t)=0.2cos(3πt) and y(1,t)=0.2cos(3πt+π8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m.
(ii) A transverse sine wave of amplitude a=0.1cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x=0.1m is shown in first figure. The shape of the string at time t=0.1s is shown in second figure. At this time the particle at x=0.11m is having velocity in positive y direction write the equation of wave.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
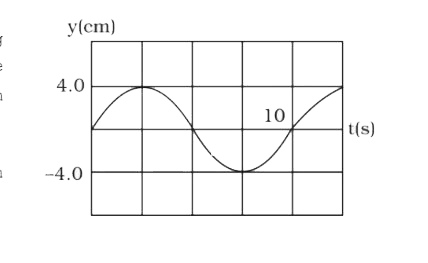
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?A−2cm/sB+2cm/sC+1.5cm/sD−2.5cm/s - Question 2 - Select One
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:A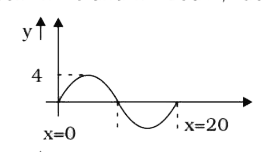 B
B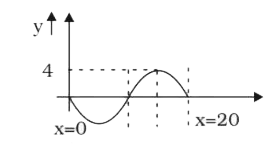 C
C D
D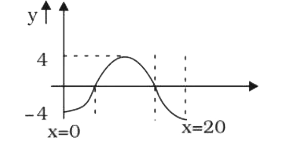
- Question 3 - Select One
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?A2cm/sB4cm/sC1cm/sD8cm/s
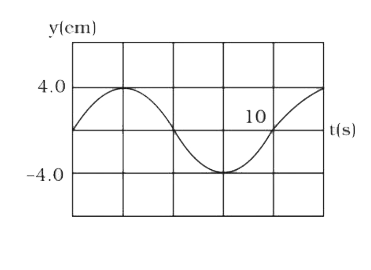
A sinusoidal transverse wave of wavelength 18 cm travels along a string in the positive direction of an x axis. The displacement y of the string particle at x= 0) is given in Fig. 16-41 as a function of time t. The scale of the vertical axis is set by y1=4.0cm, The wave equation is to be in the form y(x,t)=ynIsin(kx±ωt+ϕ). (a) At t= 0), is a plot of y versus x in the shape of a positive sine function on a legative sinc function? What are (b)ynI(c)k,(d)ω(e)ϕ, (f) the sign in front of ω, and (g) the speed of the wave? (h) What is the transverse velocity of the particle at x=0 when t=5.0 s?
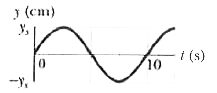 View Solution
View SolutionA transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.
View SolutionIn a standing wave 4 nodes and 3 antinodes are formed between two fixed end of string of length 6 m. Then the wave length of the standing wave is
View SolutionA standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
 View Solution
View Solution

