In an isobaric process (λ is adiabatic exponent of the gas)
The heat given to gas is λλ−1 times the work done by gas.
The work done by gas is (λ−1) time the change in internal energy.
The temperature of gas in increased.
The temperature of gas is decreased.
At constant pressure.
If volume increases. Temperature also increases
volume decreases,
In isobaric process,
ΔQ=λ.ΔU
∴ΔQ=ΔU+ΔW
∴ΔW=λ.ΔU−ΔU=(y−1)ΔU
ΔW=(y−1)ΔU
∴ΔQ=λ(y−1)ΔW
Topper's Solved these Questions
Similar Questions
One mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
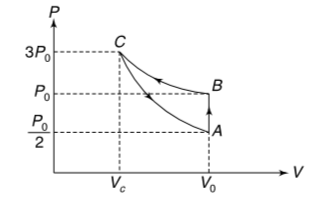
View SolutionFind the molar heat capacity of an ideak gas in a polytropic process pVn=const if the adiabatic exponent of the gas is equal to γ. At what values of the polytropic constant n will the heat capacity of the gas be negative ?
View Solution
Knowledge Check
In isobaric process
Asize of the bar remains sameBsize of barometer remains sameCpressure of the system remains sameDvolume remains sameIn an isobaric process, __________ .
Asize of the bar remains sameBsize of barometer remains sameCpressure of the system remains sameDvolume remains sameAdiabatic exponent of a gas is equal to
ACP×CVBCPCVCCP−CVDCP+CV
n moles of an ideal mono atomic gas is initially at pressure 32P0 and volume V0. Its volume is doubled by an isobaric process. After this the gas is adiabatically expanded so as to make its volume 16V0. Now the gas is isobarically expanded. Finally, the gas is made to return to its initial state by an isothermal process.
(a) Represent the process on a P–V diagram.
(b) Calculate work done by the gas in one cycle.
View SolutionIf 3 moles of H2 gas is mixed with 2 moles of helium gas, then calculate equivalent molar mass of the gas and adiabatic exponent of the mixture?
View SolutionWhich of the following is state function (a)q+w,(b)q(c )w(d) heating isobaric process (e) work in adiabatic process :-
View Solution
n moles of a monoatomic gas undergoes a cyclic process ABCDA as shown. Process AB is isobaric, process BC is adiabatic process CD is isochoric and process DA is isothermal the maximum temperature and minimum temperature in cycle are 4T0 and T0 respectively. Then:
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
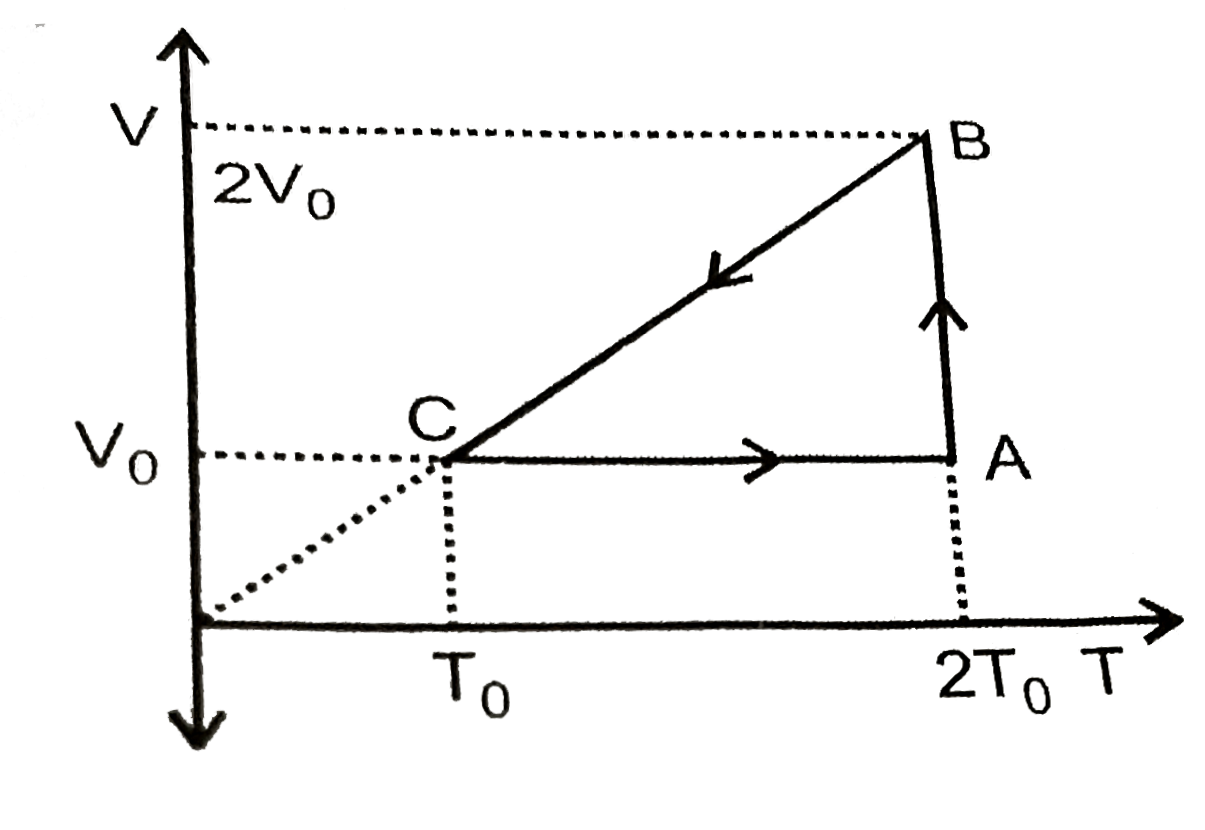
View Solution
