The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

A

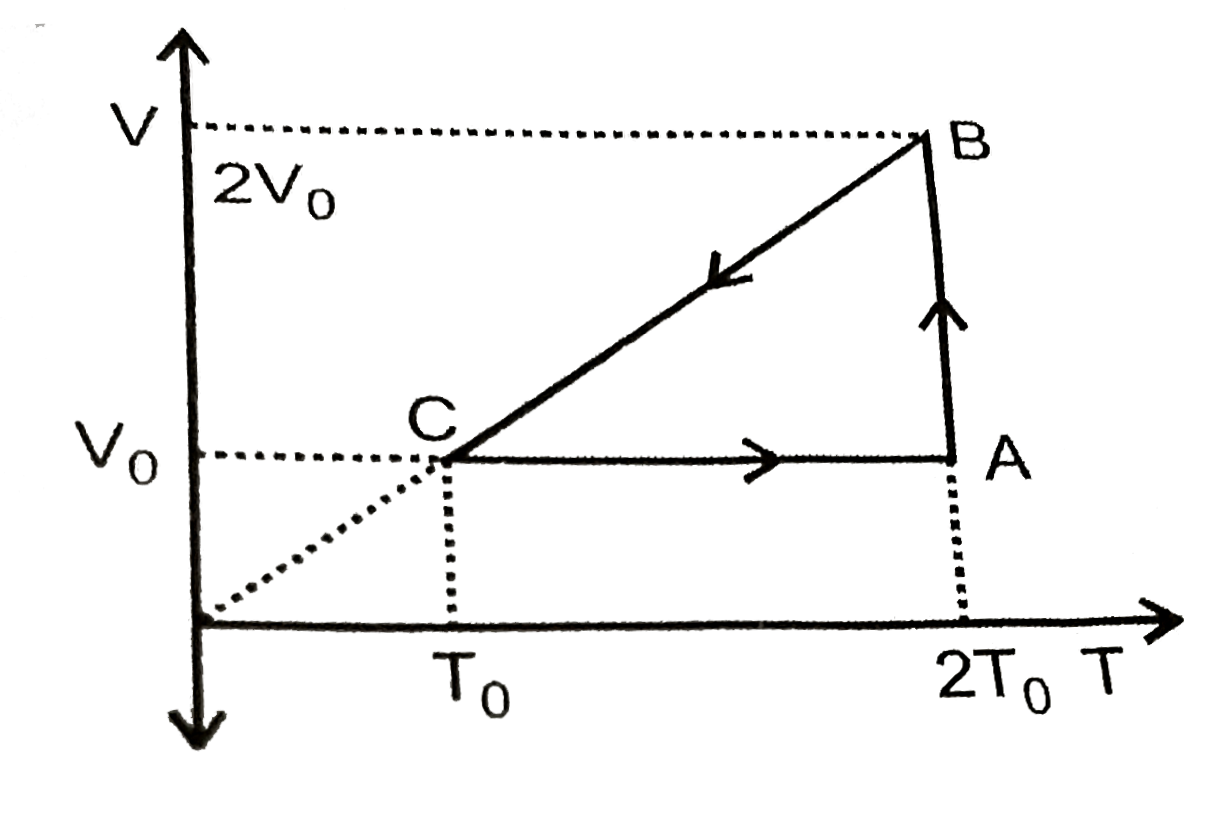
$\frac{(γ - 1) (2 ln 2 - 1)}{1 + (γ - 1) 2 ln 2}$

B

$\frac{(γ - 1) (1 - 2 ln 2)}{(γ - 1) 2 ln 2 - 1}$

C

$\frac{(2 ln 2 + 1) (γ - 1)}{(γ - 1) 2 ln 2 + 1}$

D

$\frac{(2 ln 2 - 1)}{γ / (γ - 1)}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

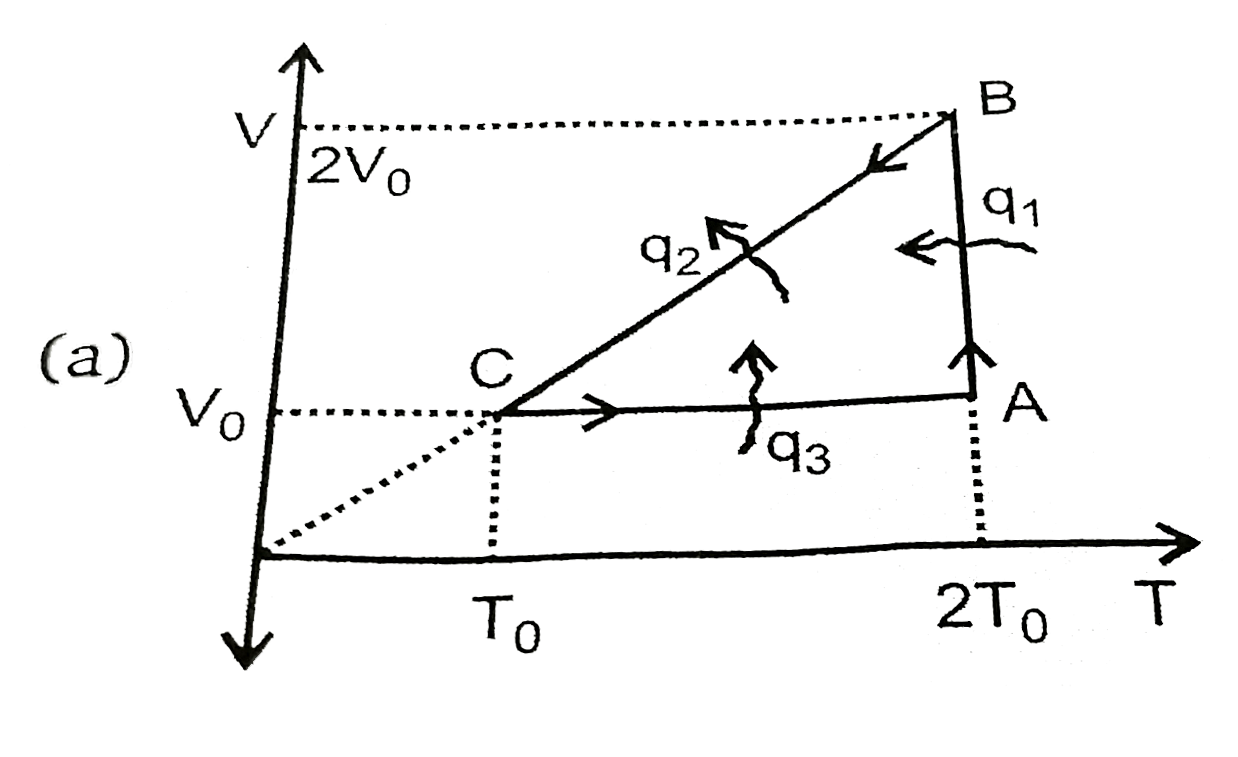
AB process
$0 = q_{1} + w_{1}$
$= q_{1} - n R (2 T_{0}) ln 2$
BC process $Δ U_{2} = q_{2} + w_{2}$
$\frac{n R}{(γ - 1)} (T_{0} - 2 T_{0}) = q_{2} - (\frac{n R T_{0}}{V_{0}}) . (V_{0} - 2 V_{0})$
CA process
$Δ U_{3} = q_{3} + w_{3}$
$\frac{n R}{(γ - 1)} (2 T_{0} - T_{0}) = q_{3} + 0$
$Efficiency = \frac{Total work done}{Total heat absorbed} = \frac{w_{1} + w_{2}}{q_{1} + q_{3}}$
$= \frac{(- 2 R T_{0} ln 2) + (n R T_{0})}{(2 R T_{0} ln 2) + (\frac{n R T_{0}}{γ - 1})}$

|

Updated on:21/07/2023

Class 11 CHEMISTRY THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Adiabatic exponent of a gas is equal to
A $C_{P} \times C_{V}$
B $\frac{C_{P}}{C_{V}}$
C $C_{P} - C_{V}$
D $C_{P} + C_{V}$
Question 2 - Select One
An ideal gas with adiabatic exponent ( $γ = 1.5$ ) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
AC=4R
BC=0
CC=2R
DC=R
Question 3 - Select One
An ideal gas with adiabatic exponent $γ$ undergoes a process in which internal energy depends on volume
as $U = a V^{α}$ then select the correct statement .
AChange in internal energy is $\frac{γ - 1}{α} Δ T$
BMolar heat capacity of process is $\frac{R}{1 - γ} + \frac{R}{α}$
CHeat exchange in the process is given by $Δ U [1 + \frac{1 - γ}{α}]$
DEquation of process is given is $P V^{x}$ =constant , where $x > 0 if α < 1$ .

NARENDRA AWASTHI-THERMODYNAMICS-Level 3 - Match The Column

Home
Ask Doubt
Profile