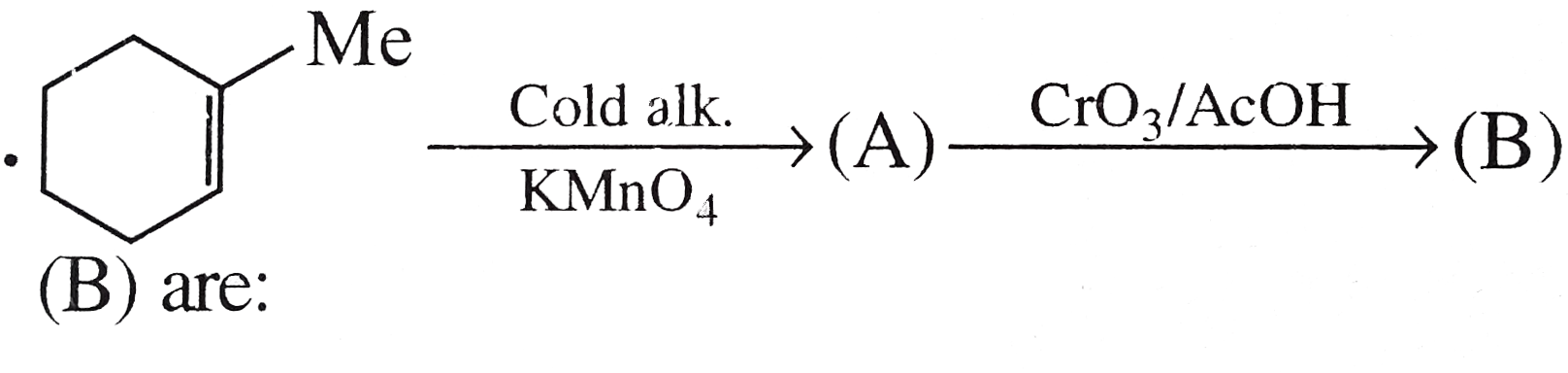
(A) and (B) are:
A
a.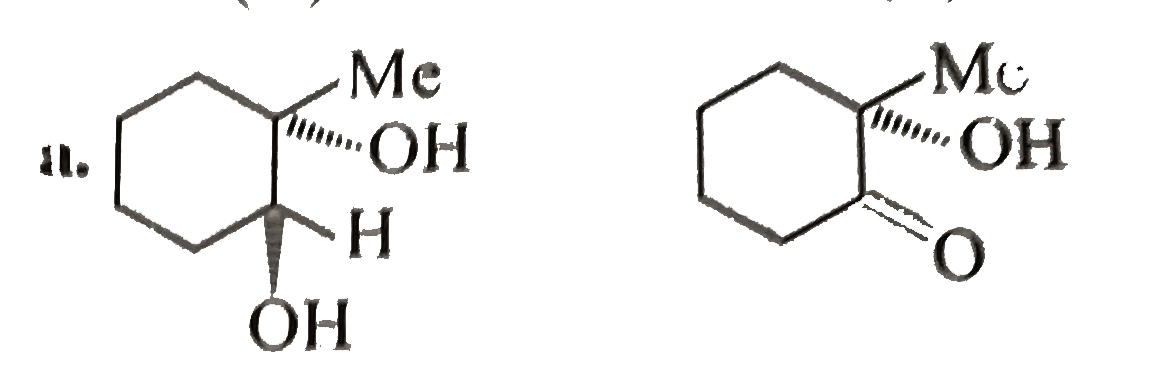
B
b.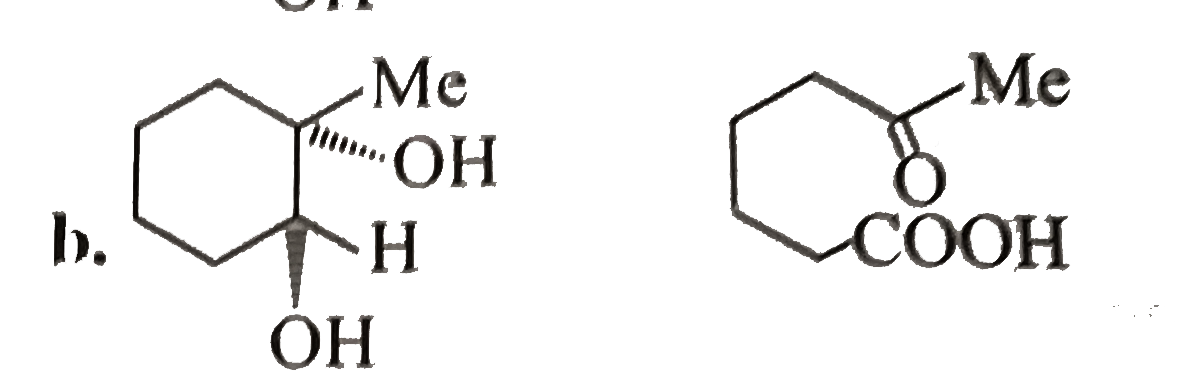
C
c.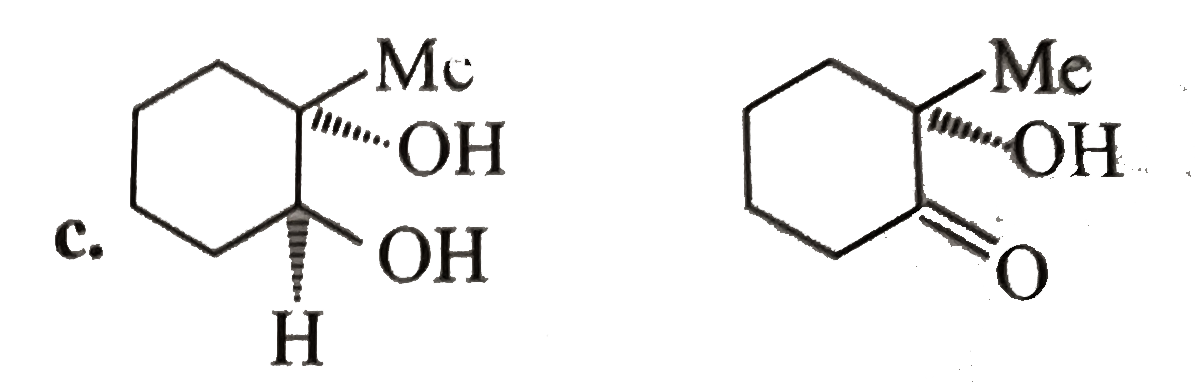
D
d.
Text Solution
The correct Answer is:A
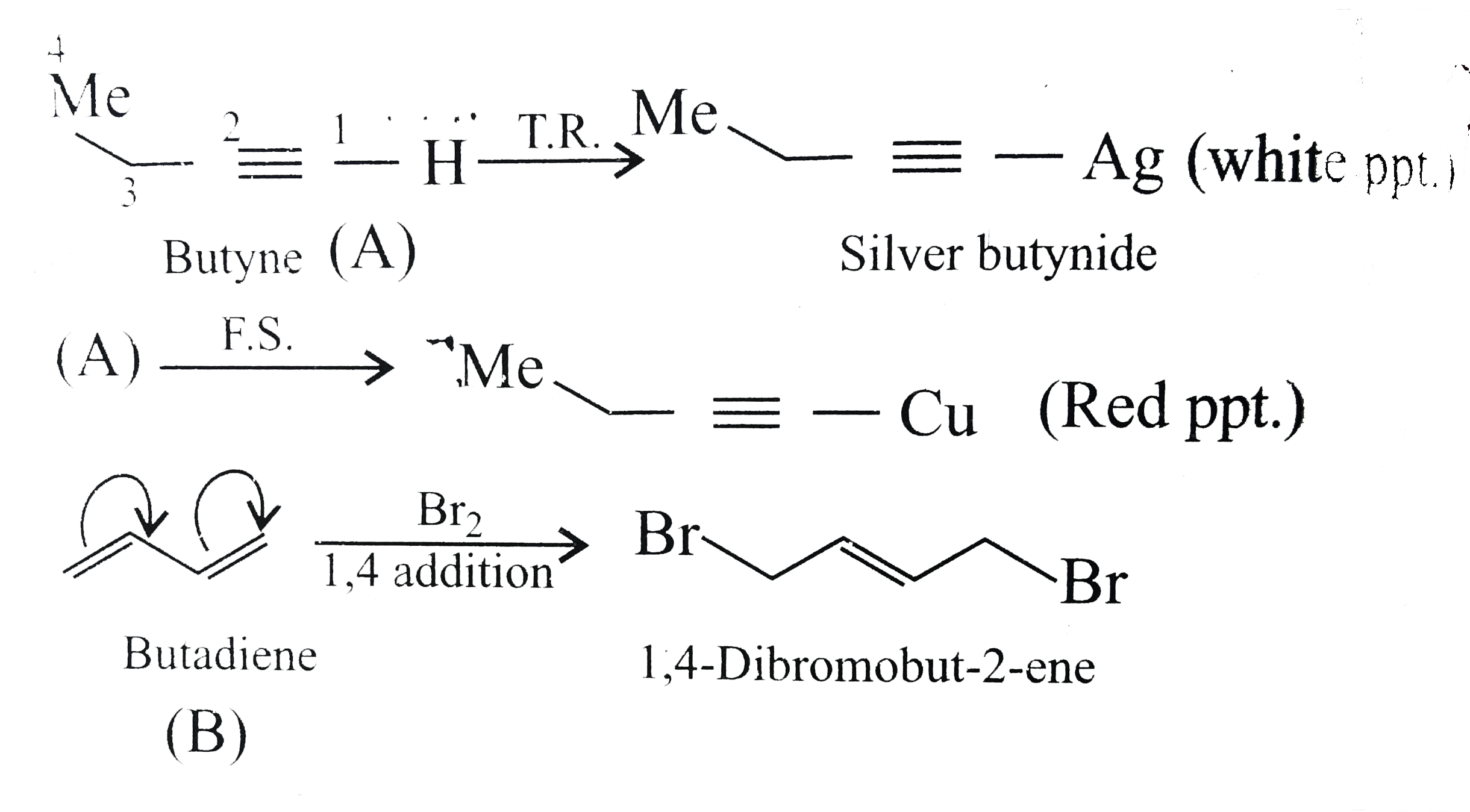
so the answer is (a).
|
Topper's Solved these Questions
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - Exercise (Assertion And Reasoning)
10 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - Exercise Archives (Subjective)
26 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - Exercise (Multiple Correct)
35 Videos
- QUALITATIVE INORGANIC SALT ANALYSISBOOK - CENGAGE CHEMISTRYCHAPTER - QUALITATIVE INORGANIC SALT ANALYSISEXERCISE - Viva Voce Questions And Part-C (Analysis Of Cations)
42 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Ex 1.2 (Objective)
9 Videos
Similar Questions
Knowledge Check
If the vectors a, b and c are coplanar, then ∣∣ ∣∣abca⋅aa⋅ba⋅cb⋅ab⋅bb⋅c∣∣ ∣∣ is equal to
A1B0C−1DNone of these 3The three points [(a+b)(a+2b),(a+b)],[(a+2b)(a+3b),(a+2b)] and [(a+3b)(a+4b),(a+3b)]
Aare collinearBform a triangle whose area is independent of aCform a triangle whose area is independent of bDform a triangle whose area is independent of a,b
If a, b and c are three coplanar vectors. If a is not parallel to b, show that c=∣∣∣c⋅aa⋅bc⋅bb⋅b∣∣∣a+∣∣∣a⋅ac⋅aa⋅bc⋅b∣∣∣b∣∣∣a⋅aa⋅ba⋅bb⋅b∣∣∣.
View SolutionIf a, b and c are three coplanar vectors. If a is not parallel to b, show that c=∣∣∣c⋅aa⋅bc⋅bb⋅b∣∣∣a+∣∣∣a⋅ac⋅aa⋅bc⋅b∣∣∣b∣∣∣a⋅aa⋅ba⋅bb⋅b∣∣∣.
View SolutionWhich of the following statement is false:
a .A−B=A−(A∩B) b. A−B=A−(A∩B) c. A−B=A−B' d. A−B=(A∪B)−B
View SolutionIf AB=AandBA=B, then a. A2B=A2 b. B2A=B2 c. ABA=A d. BAB=B
View SolutionIf a,b∈R and a⋅b=aa+b where a+b≠0 and a⋅b=5 then b⋅a=
View SolutionThe product of a and b is added to their sum is written as
(a)ab+a+b
(b) a+b−ab
(c) a+ab
(d) a+ab−b
View Solution