ABCD is a rhombus. Its diagonals ACandBD intersect at the point M and satisfy BD=2AC.If he point DandM represent the complex numbers 1+iand2−i respectively, then A represents the complex number......or......
Step by step video & image solution for ABCD is a rhombus. Its diagonals AC and BD intersect at the point M and satisfy BD = 2AC.If he point D and M represent the complex numbers 1 + i and 2 - i respectively, then A represents the complex number......or...... by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Exercise For Session 1
6 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Exercise For Session 2
14 Videos
- CIRCLE BOOK - ARIHANT MATHSCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
16 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
Similar Questions
Knowledge Check
In a given parallelogram, if the points P1 and P2 represent two complex numbers z1 and z2, then the point P3 represents the number
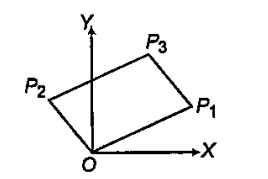 Az1+z2Bz1−z2Cz1×z2Dz1+z2
Az1+z2Bz1−z2Cz1×z2Dz1+z2In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax - y - 1 = 0Bx + y - 1 = 0Cx - y + 1 = 0Dx + y - 7 =0The points represented by the complex numbers 1+i,−2+3i and 53i on the argand diagram are
AVertices of an equilateral triangleBVertices of an isosceles triangleCCollinearDNone of the above
If |z|=2 then the points representing the complex number −1+5z will be
View SolutionABCD is a rhombus whose diagonals intersect at O. If AB=10cm, diagonals BD=16 cm , find the length of diagonal AC
View SolutionThe points A,B and C represent the complex numbers z1,z2,(1−i)z1+iz2 respectively, on the complex plane (where, i=√−1). The △ABC, is
View SolutionIn a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
View SolutionThe points represented by the complex numbers 1+i,−2+3i and 53i on the argand diagram are
View Solution
