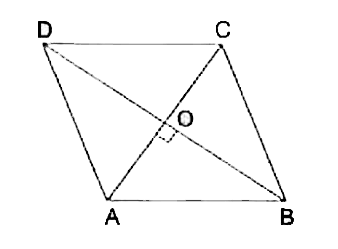
is a rhombus whose diagonals intersect at If diagonals , find the length of diagonal
To find the length of diagonal AC in the rhombus ABCD, we can follow these steps:
Step 1: Understand the properties of the rhombus
In a rhombus, the diagonals bisect each other at right angles (90 degrees). This means that if diagonals BD and AC intersect at point O, then AO and OC are equal, and BO and OD are equal.
Step 2: Identify the lengths given
We are given:
- AB = 10 cm (the length of one side of the rhombus)
- BD = 16 cm (the length of diagonal BD)
Step 3: Calculate the lengths of the segments of diagonal BD
Since the diagonals bisect each other, we can find the lengths of segments BO and OD:
- BO = OD = BD / 2 = 16 cm / 2 = 8 cm
Step 4: Set up the right triangle
Now, we can focus on triangle AOB, which is a right triangle (since the diagonals intersect at right angles). We know:
- AB (hypotenuse) = 10 cm
- BO (one leg) = 8 cm
- AO (the other leg, which we need to find)
Step 5: Apply the Pythagorean theorem
According to the Pythagorean theorem:
AB2=AO2+BO2
Substituting the known values:
102=AO2+82
100=AO2+64
Step 6: Solve for AO
Now, we can isolate AO^2:
AO2=100−64
AO2=36
Taking the square root of both sides:
AO=6 cm
Step 7: Find the length of diagonal AC
Since diagonal AC is made up of two segments AO and OC, and AO = OC:
AC=2×AO=2×6=12 cm
Final Answer
The length of diagonal AC is 12 cm.
---
In a rhombus, the diagonals bisect each other at right angles (90 degrees). This means that if diagonals BD and AC intersect at point O, then AO and OC are equal, and BO and OD are equal.
We are given:
- AB = 10 cm (the length of one side of the rhombus)
- BD = 16 cm (the length of diagonal BD)
Since the diagonals bisect each other, we can find the lengths of segments BO and OD:
- BO = OD = BD / 2 = 16 cm / 2 = 8 cm
Now, we can focus on triangle AOB, which is a right triangle (since the diagonals intersect at right angles). We know:
- AB (hypotenuse) = 10 cm
- BO (one leg) = 8 cm
- AO (the other leg, which we need to find)
According to the Pythagorean theorem:
AB2=AO2+BO2
Substituting the known values:
102=AO2+82
100=AO2+64
Now, we can isolate AO^2:
AO2=100−64
AO2=36
Taking the square root of both sides:
AO=6 cm
Since diagonal AC is made up of two segments AO and OC, and AO = OC:
AC=2×AO=2×6=12 cm
The length of diagonal AC is 12 cm.
Topper's Solved these Questions
Similar Questions
ABCD is a rhombus whose diagonals intersect at O. If AB=10cm, diagonals BD=16 cm , find the length of diagonal AC
View SolutionIn the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
View Solution
Knowledge Check
If the perimeter of a rhombus is 56 cm and the length of one of its diagonals is 26 cm. then find the length of the other diagonal of the rhombus.
A)6√7 cm
B)6√5 cm
C)6√3 cm
D)6√2 cmA6√7 cmB6√5 cmC6√3 cmD6√2 cmThe side of a rhombus is 10 cm. The smaller diagonal is 13 of the greater diagonal. Find the length of the greater diagonal.
A6√10cmB10√6cmC6√5cmD5√6cm
Each side of a rhombus is 10cm. If one of its diagonals is 16cm find the length of the other diagonal.
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠B as well as ∠D.
View Solution
