For positive l, m and n, if the points x=ny+mz,y=lz+nx,z=mx+ly intersect in a straight line, when
Q. l, m and n satisgy the equation
l2+m2+n2=2
l2+m2+n2+2mln=1
l2+m2+n2=1
None of these
The correct Answer is:(b)
Topper's Solved these Questions
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Single Integer Answer Type Questions)
26 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Subjective Type Questions)
9 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Statement I And Ii Type Questions)
14 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
Knowledge Check
For positive l, m and n, if the planes x=my+mz,y=1z+nx,z=mx+1y intersect in a straight, line, then:
1, m and n satisfy the equation:A12+m2+n2=2BI2+m2+n2+2ln=1CI2+m2+n2=1DNone of theseFor positive l, m and n, if the planes x=my+mz,y=1z+nx,z=mx+1y intersect in a straight, line, then:
The equation of the straight line is xa=yb=zc, where the ordered traid (a,b,c) is :A√1−l2,√1−m2,√1−n2B1,m and nC1√1−I2,m√1−m2andn√1−n2DNone of theseFor positive l, m and n, if the points x=ny+mz,y=lz+nx,z=mx+ly intersect in a straight line, when
Q. cose−1(l)+cos−1(m)+cos−1(n) is equal toA90∘B50∘C180∘DNone of these
n,l,m are three lines in the same plane. If l intersects m and nllm, then find the relation betweenl and n.
View SolutionLet PQ be a line segment with P(x1,y1,z1)andQ(x2,y2,z2) and let L. be a straight line whose d.c.'s are l, m, n. Then the length of projection of PQ on the line L is
View SolutionIn figure P is a point equidistant from the lines l and m intersecting at point A. Show that the line n (along AP) bisects the angle between l and m.

View SolutionOf all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
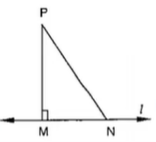
View SolutionOf all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
View Solution
