Show that the triangle, the coordinates of whose verticles are given by integers, can never be an equilateral triangle.
The correct Answer is:c=±b√3
Step by step video, text & image solution for Show that the triangle, the coordinates of whose verticles are given by integers, can never be an equilateral triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 110videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 219videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)20videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)38videos
DEFINITE INTEGRAL
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ?
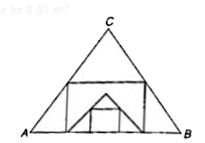 Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of these
Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of these - Question 2 - Select One
In the given figure, ΔABC is an equilateral triangle. Find ∠BEC :
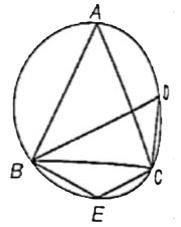 A120∘B60∘C80∘Dnone of the above
A120∘B60∘C80∘Dnone of the above
If the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf (-4,3) and (4,3) are two vertices of an equilateral triangle, then find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
View SolutionIn the given figure, OP is equal to the diameter of the circle. Prove that △ABP is an equilateral triangle.
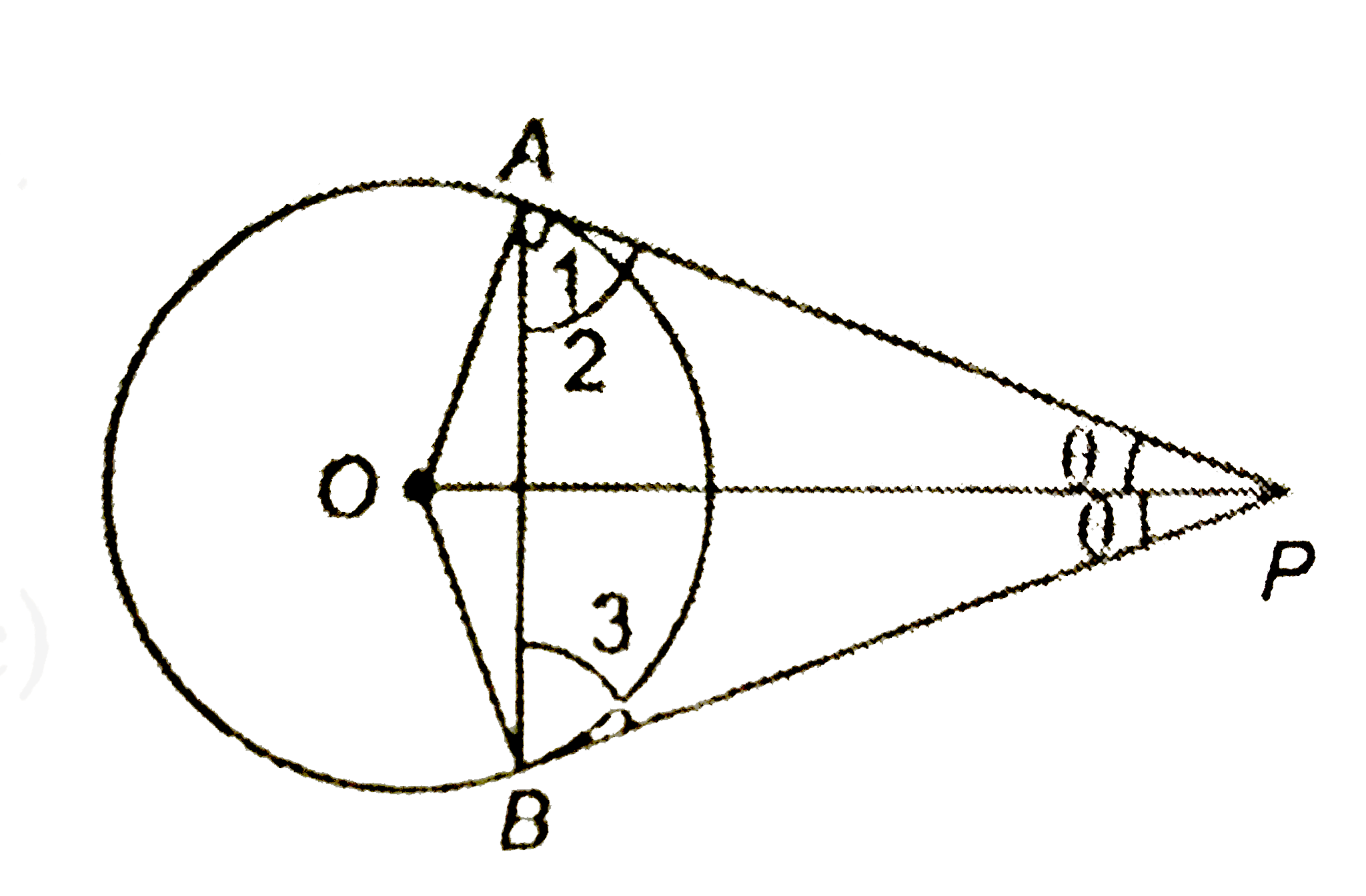 View Solution
View SolutionIf the vertices of a triangle have integral coordinates, prove that the trinagle cannot be equilateral.
View SolutionFind the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View Solution

