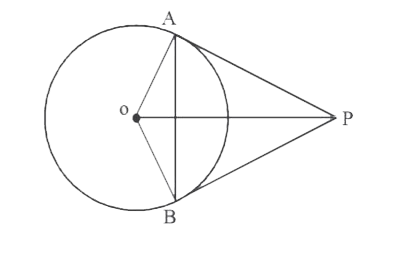
In the given figure, OP is equal to the diameter of the circle. Prove that $△ A B P$ is an equilateral triangle.

Video Solution

Text Solution

Verified by Experts

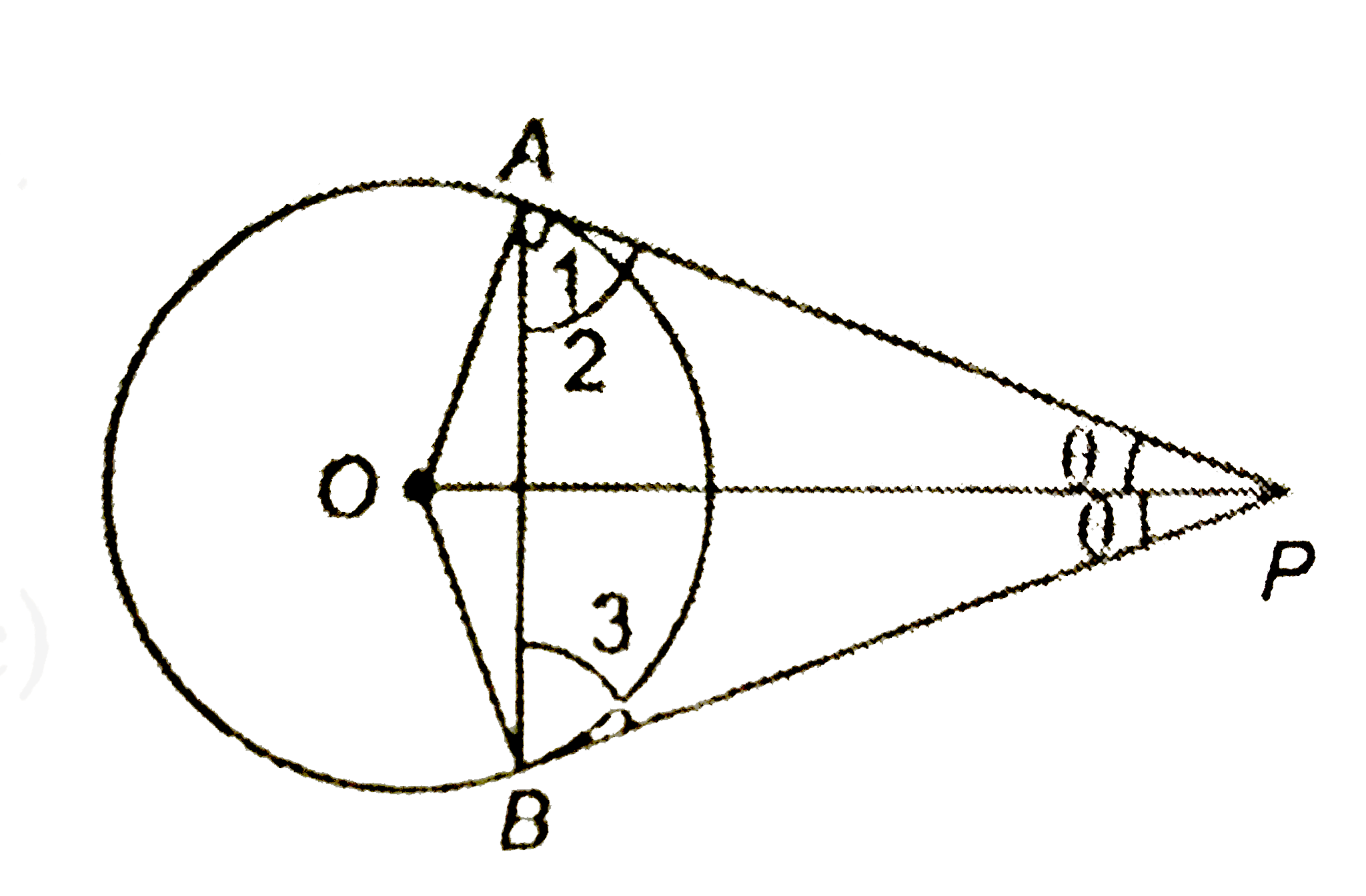
Let $∠ O P = ∠ O P B = θ$
( $∵$ tangents are equally inclined at the centre)
and radius of the circle be r.
Since, $∠ 1 = 90^{\circ}$ (radius through point of contact is $⊥$ to the tangent)
$∴$ In right $△ O A P,$
$sin θ = \frac{O A}{O P} = \frac{r}{2 r} = \frac{1}{2} = {sin 30}^{\circ}$
$∴ θ = 30^{\circ} \Rightarrow ∠ A P B = 20 = 2 \times 30^{\circ} = 60^{\circ}$ ...(1)
Now, since $P A = P B$ (length of tangents from an external point are equal)
$∴ ∠ 2 = ∠ 3$ (angles opposite to equal sides are equal)" "...(2)
In $△ A P B,$
$∠ 2 + ∠ 3 + ∠ A P B = 180^{\circ}$ (angle sum property)
$\Rightarrow ∠ 2 + ∠ 2 + 60^{\circ} = 180^{\circ}$ [from (1) and (2)]
$\Rightarrow 2 ∠ 2 = 120^{\circ} \Rightarrow ∠ 2 = 60^{\circ}$
$∴ ∠ 2 = ∠ 3 = 60^{\circ}$
So, all the angles of $△ A P B$ are $60^{\circ} .$
$∴ △ A P B$ is an equilateral triangle. Hence Proved.

|

Updated on:21/07/2023

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the ratio of the diameter of the circles inscribed and circumscribing an equilateral triangle to its height
A $1 : 2 : 1$
B $2 : 4 : 3$
C $1 : 3 : 4$
D $3 : 2 : 1$

NAGEEN PRAKASHAN-CIRCLES-Revision Exercise Long Answer Questions

Home
Ask Doubt
Profile