Let f(x)=x2+3x−3,x≤0. If n points x1,x2,x3,.....,xn are so chosen on the x-axis such that
The correct Answer is:1nn∑i=1xi=1
Step by step video, text & image solution for Let f(x)=x^2 + 3x-3,x leq 0. If n points x_1, x_2, x_3,.....,x_n are so chosen on the x-axis such that by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
24 Videos
- FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - FUNCTIONSEXERCISE - Exercise (Single Integer Answer Type Questions)
31 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHSCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHSCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
Knowledge Check
Let f(x)=x2+3x−3,x≥0 if in points x1,x2,x3,...xn are so chosed on the x-axis such that
(i) 1nn∑i=1f−1(xi)=f(1nn∑i=1xi)
(ii) n∑i=1f−1(xi)=n∑i=1xi wehre f−1 denots the inverser of f. then mean of x1,x2,x3,....xn is :A1B2C3D4Let f(x)=x3+32x2+3x+3, then f(x) is
Aa decreasing functionBan increasing functionCan odd functionDan even function
The following functions are defined for the set of variables x1,x2,x3,.......,xn
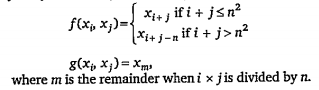
Find the value of f(f(x2,x3),f(x5,x6)) if n=3
View SolutionLet f(x)= x4−3x3+2x2−3x+a.If f(√−1)=0 and a∈R then prove that f (x) < 0 for x∈(1,2).
View SolutionLetf(x)=x2+x+1x2+3x+3xx∈R . Let m be the mid-point of the range of f(x) , then 3m + 2 . 31 is equal to _______
View SolutionLet f(x) =x3−3x+2. Examine the monotonicity of function at points x=0.1,2
View SolutionLet f(x)={1+x,0≤=x≤=2and3−x,2<x≤3' find (fof)(x).
View SolutionIf f(x)=sgn(x−2)×[Inx],1≤x≤3and{x2},−3<x≤3.5 where [.] denotes the greatest integer function and {.} represents the fractional part functon, then the number of points of discontinuity in [1,3.5] is
View Solution
