Let f(x)=x2+3x−3,x≤0. If n points x1,x2,x3,.....,xn are so chosen on the x-axis such that
Step by step video & image solution for Let f(x)=x^2 + 3x-3,x leq 0. If n points x_1, x_2, x_3,.....,x_n are so chosen on the x-axis such that by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Let f(x)=x2+3x−3,x≥0 if in points x1,x2,x3,...xn are so chosed on the x-axis such that
(i) 1nn∑i=1f−1(xi)=f(1nn∑i=1xi)
(ii) n∑i=1f−1(xi)=n∑i=1xi wehre f−1 denots the inverser of f. then mean of x1,x2,x3,....xn is :A1B2C3D4
Let f(x)=|3−|2−|x−1|∣∣,∀x∈R be not differentiable at x1,x2,x3,….xn , then n∑i=1x2i equal to :
View SolutionThe following functions are defined for the set of variables x1,x2,x3,.......,xn
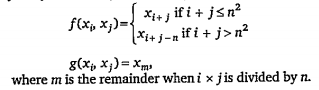
Find the value of f(f(x2,x3),f(x5,x6)) if n=3View SolutionLet f(x)= x4−3x3+2x2−3x+a.If f(√−1)=0 and a∈R then prove that f (x) < 0 for x∈(1,2).
View SolutionLetf(x)=x2+x+1x2+3x+3xx∈R . Let m be the mid-point of the range of f(x) , then 3m + 2 . 31 is equal to _______
View SolutionLet f(x)=1+x, 0≤x≤2 and f(x)=3−x,2<x≤3. Find f(f(x)).
View SolutionLet f(x) =x3−3x+2. Examine the monotonicity of function at points x=0.1,2
View SolutionLet f(x) =x3−3x+2. Examine the monotonicity of function at points x=0.1,2
View Solution

