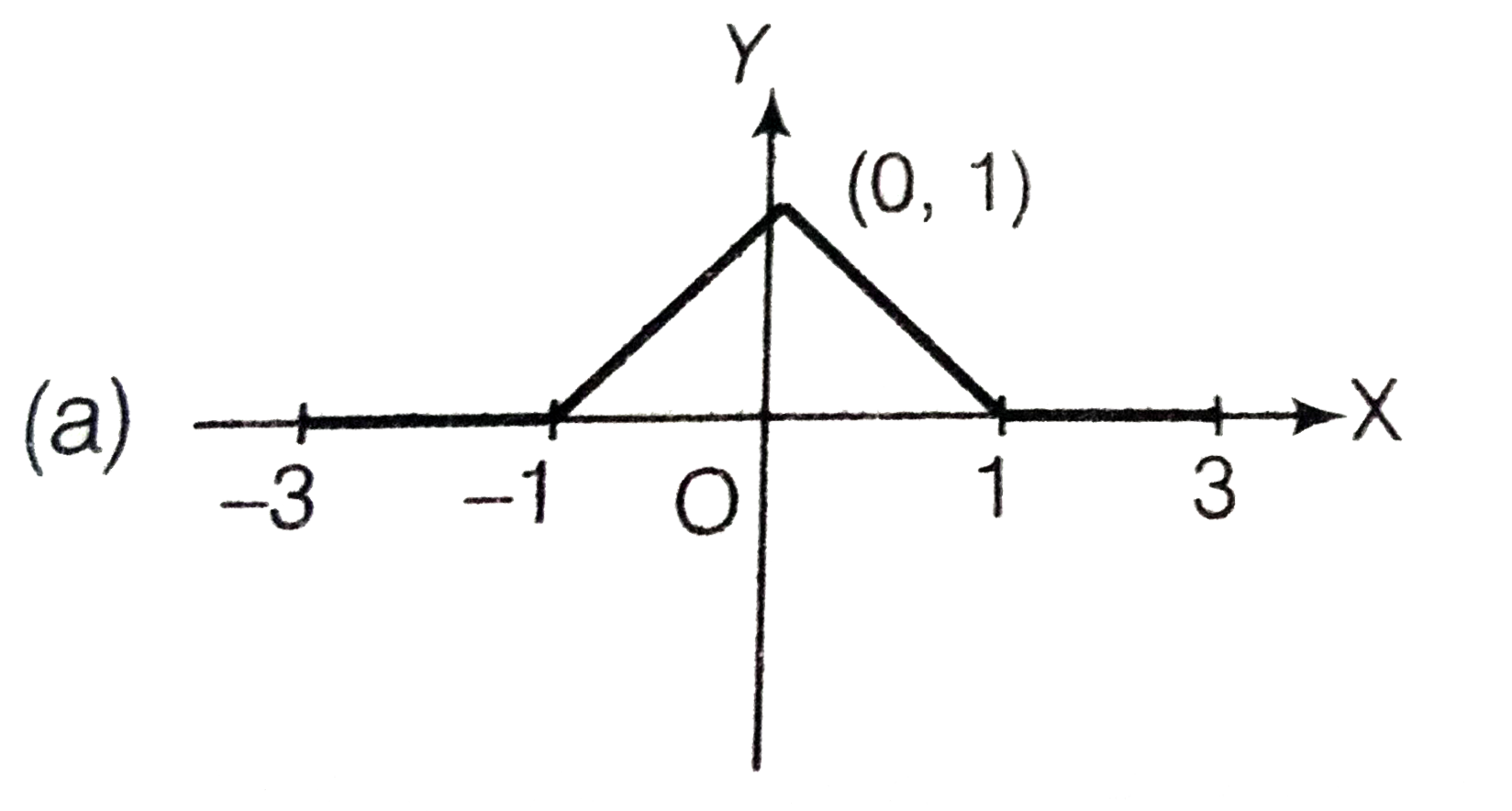
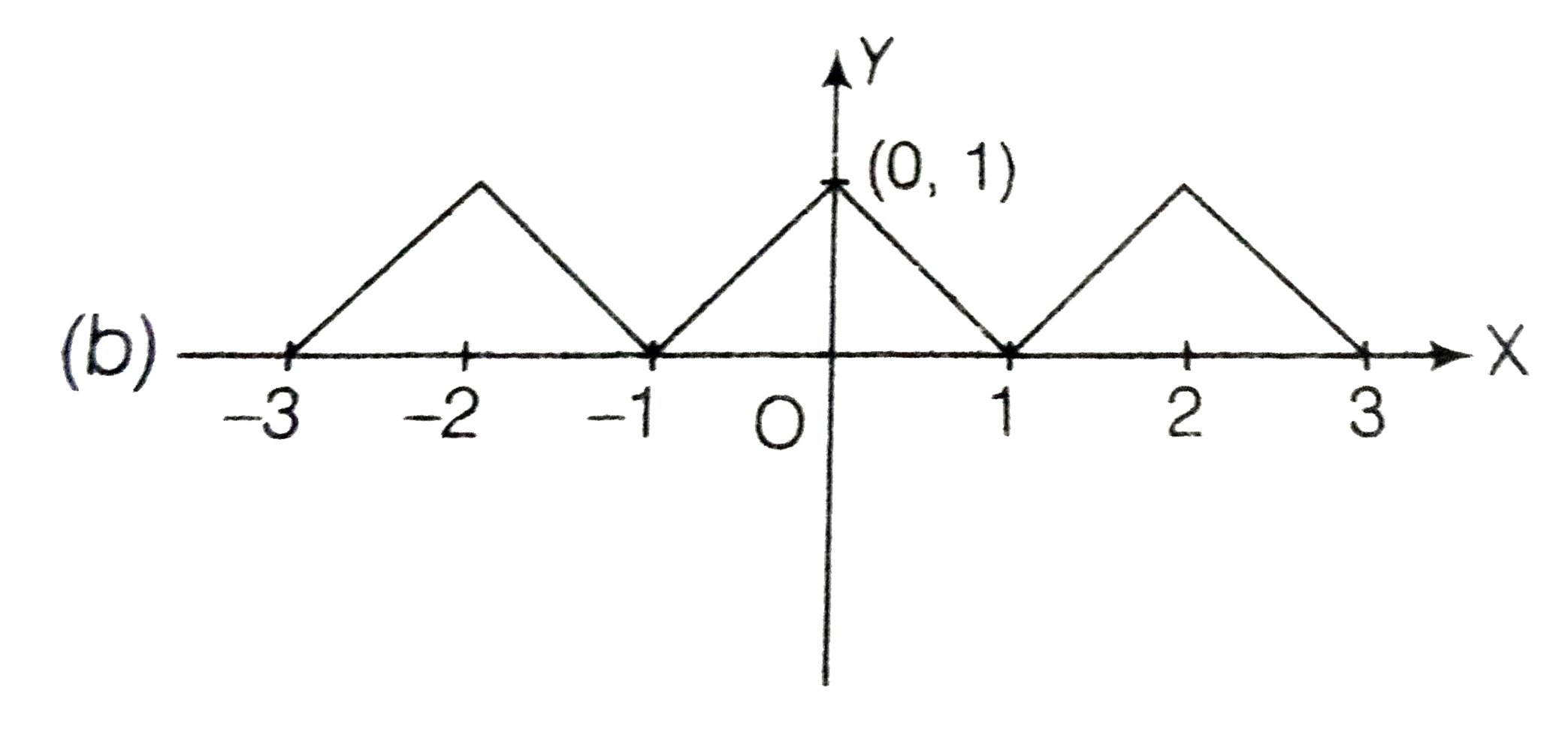
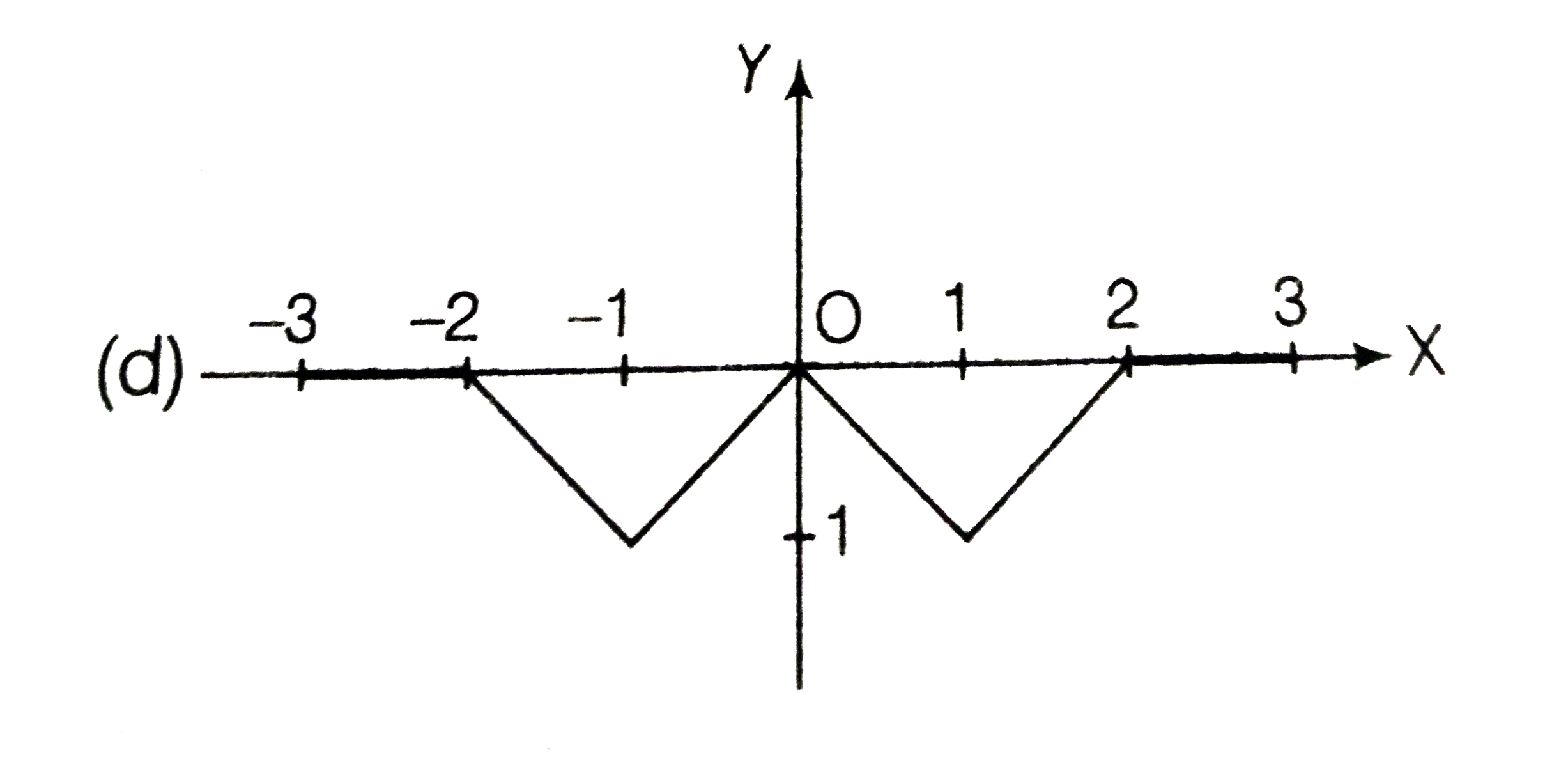
Let $f (x) = {\begin{matrix} 1 - | x |, | x | \leq 1 0, | x | > 1 \end{matrix} and g (x) = f (x - 1) for all x \in R$ The graph for g(x) is given by

ocr_image

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Let $f (x) = {\begin{matrix} - 1, - 2 \leq x < 0 x^{2} - 1, 0 \leq x \leq 2 \end{matrix}$ and $g (x) = | f (x) | + f (| x |)$ . Then in the interval $(- 2, 2)$ , g is
Adifferentiable at all points
Bnot differentiable at two points
Cnot continuous
Dnot differentiable at one point
Let $g (x) = 1 + x - [x] and f (x) = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} - 1, & x < 0 0, & x = 0 1, & x > 0 \end{matrix}$ , then for all $x, f [g (x)]$ is equal to
Ax
B1
C $f (x)$
D $g (x)$
Let $g (x) = 1 + x - [x]$ and $f (x) = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} - 1, & x < 0 0, & x = 0 1, & x > 0 \end{matrix}$ , then for all $x$ , $f [g (x)]$ is equal to
A $x$
B $1$
C $f (x)$
D $g (x)$