Let f(x)={1−|x|,|x|≤1and0,|x|<1andg(x)=f(x−)+f(x+1), for all x∈R.Then,the value of ∫3−3g(x)dx is
2
3
4
5
The correct Answer is:A
Step by step video, text & image solution for Let f(x)={1-|x|,|x| leq 1 and 0,|x| lt 1 and g(x)=f(x-)+f(x + 1), for all x in R.Then,the value of int_-3^3 g(x)dx is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 520videos
DEFINITE INTEGRAL
- BOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 610videos
DEFINITE INTEGRAL
- BOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 320videos
DEFINITE INTEGRAL
- BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHSCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
DETERMINANTS
Similar Questions
Knowledge Check
- Question 1 - Select One
Let f(x)={1−|x|,|x|≤10,|x|>1andg(x)=f(x−1)for allx∈R The graph for g(x) is given by
A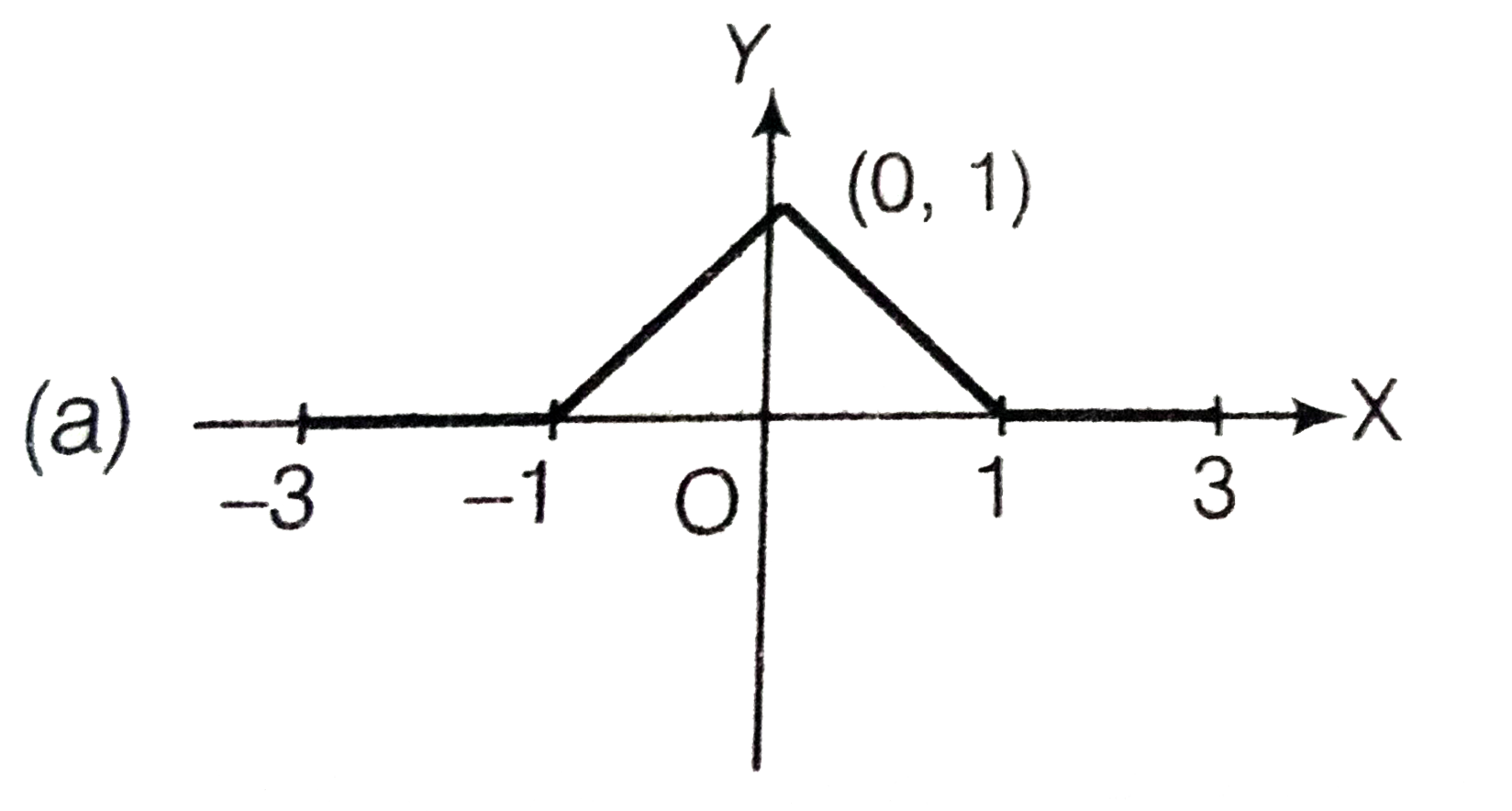 B
B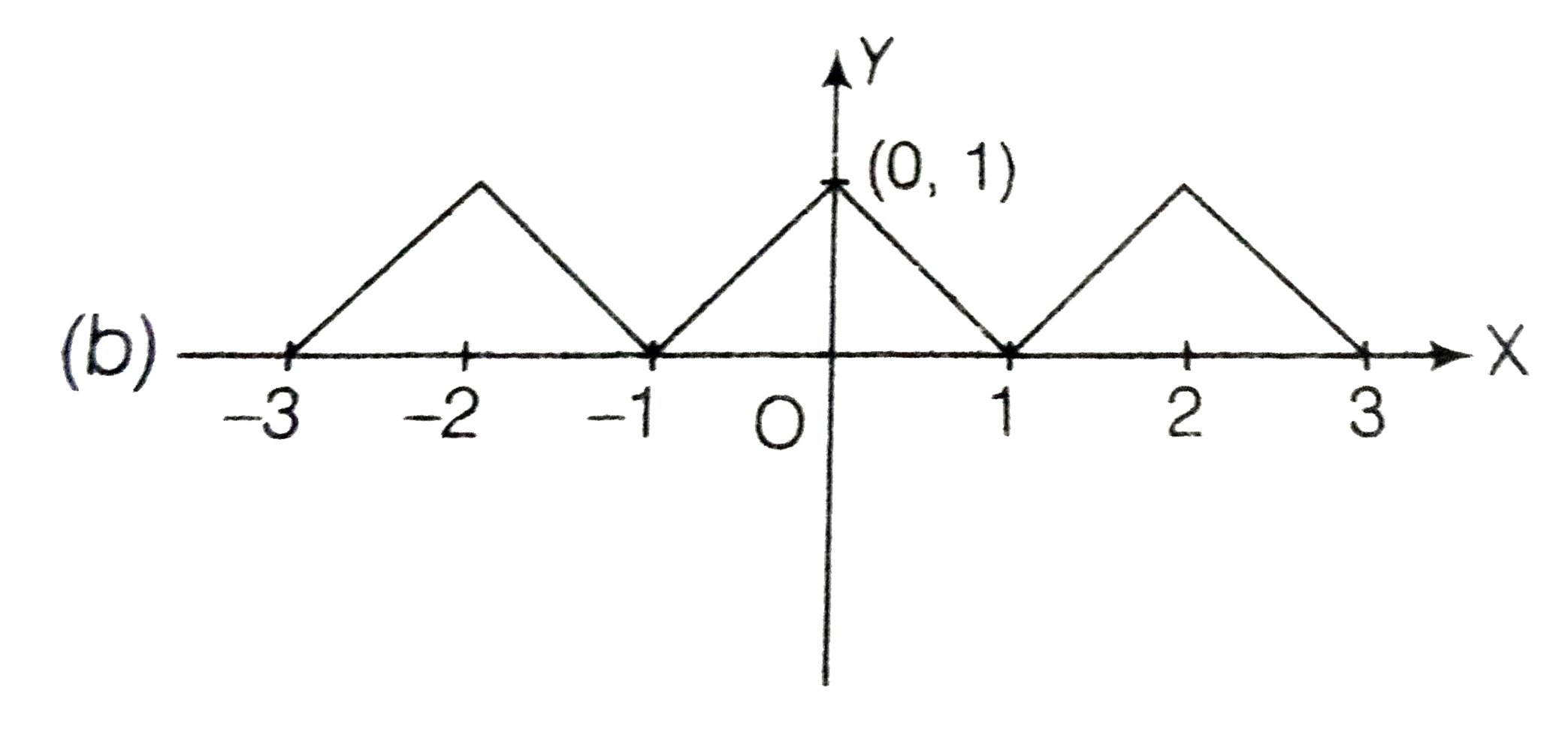 C
C D
D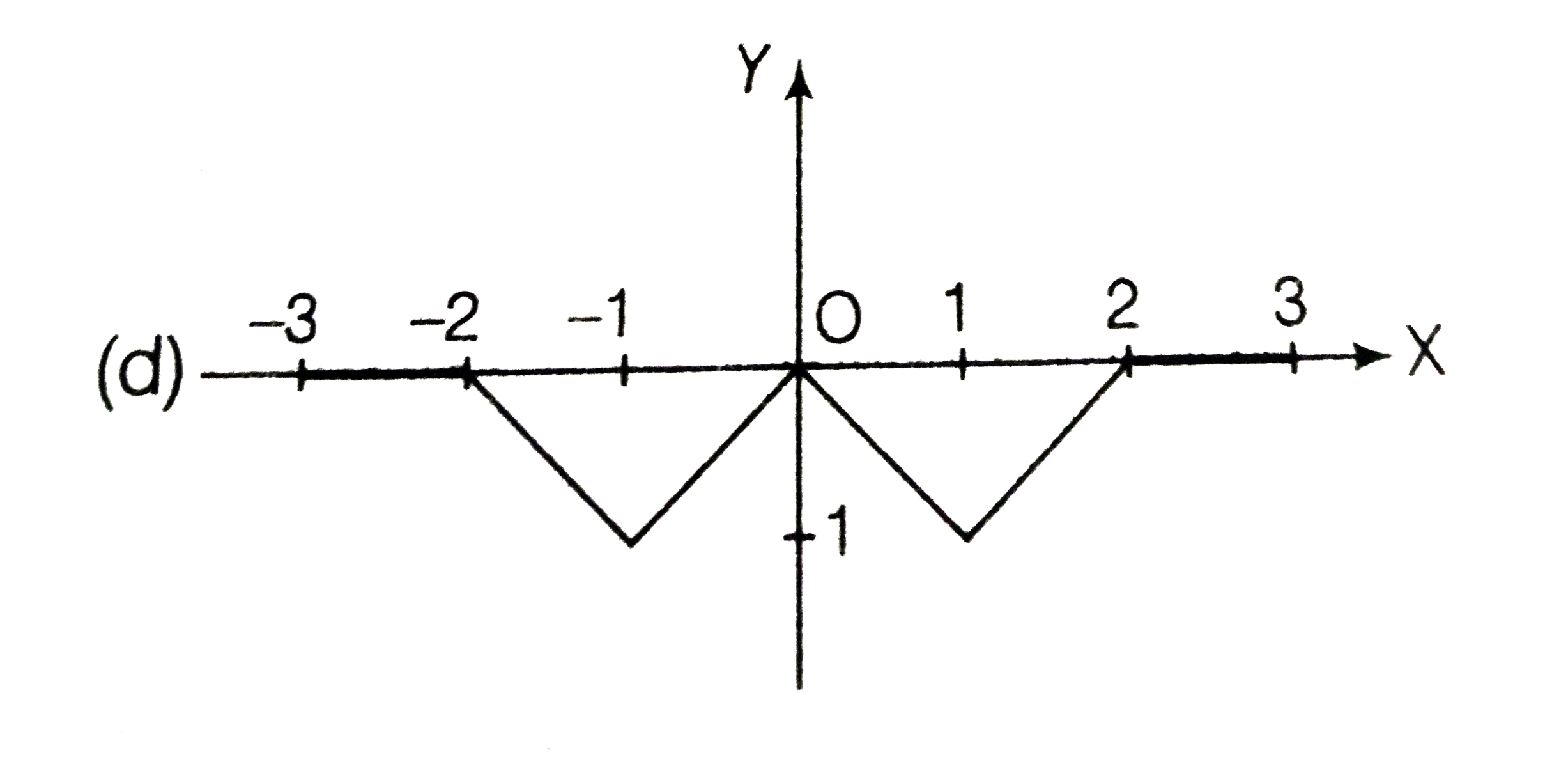
- Question 2 - Select One
Let f:R→R be continuous function such that f(x)=f(2x) for all x∈R. If f(t)=3, then the value of ∫1−1f(f(x))dx, is
A3f(0)B0C3f(3)D6 - Question 3 - Select One
Let g(x)=f(x)+f'(1−x)andf''(x)<0,0≤x≤1 Then
Ag(x) increases on [0,1]Bg(x) increases on [0,1]Cg(x) increases on [0,1]Dg(x) increases on [0,1/2] and decreases on [1/2,1]
Let f(x)=minimum {|x|,1−|x|,14} for xεR then the value of ∫1−1f(x)dx is equal to
View SolutionLet the function f be defined by
f(x)=|x−1|−12,0≤x≤2,f(x+2)=f(x) for all x∈R.
Evaluate (i)∫1000f(x)dx
(ii) ∫10|f(2x)|dxView Solutionlet (f(x)=1−|x|,|x|≤1,0,|x|>1) g(x)=f(x+1)+f(x−1)
View SolutionIf f(x)=x2g(x)andg(1)=6,g'(x)3, find the value of f' (1).
View SolutionLet f(x) be a continuous function such that f(a-x)+f(x)=0 for all x∈[0,a]. Then, the value of the integral
∫a011+ef(x)dx is equal toView Solution

