The circle inscribed in the triangle ABC touches the side BC, CA and AB in the point A1B1andC1 respectively. Similarly the circle inscribed in the ΔA1B1C1 touches the sieds in A2,B2,C2 respectively and so on. If AnBnCn be the nth Δ so formed, prove that its angle are
(C−π3). Hence prove that the triangle so formed is ultimately equilateral.
The correct Answer is:An=Bn=Cn=π3.
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 2
19 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
The circle inscribed in the triangle ABC touches the side BC, CA and AB in the point A1B1andC1 respectively. Similarly the circle inscribed in the ΔA1B1C1 touches the sieds in A2,B2,C2 respectively and so on. If AnBnCn be the nth Δ so formed, prove that its angle are
π3−(2)−n(A−π3),π3−(2)−n(B−π3),π3−(2)−n(C−π3). Hence prove that the triangle so formed is ultimately equilateral.
View SolutionLet the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. limn→∞∠An=
View Solution
Knowledge Check
Let the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. limn→∞∠An=A0Bπ6Cπ4Dπ3Let the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. limn→∞∠An=A0Bπ6Cπ4Dπ3Let the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. In ΔA4B4C4, the value of ∠A4 is:A3π+A6B3π−A8C5π−A16D5π+A16
Let the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. In ΔA4B4C4, the value of ∠A4 is:
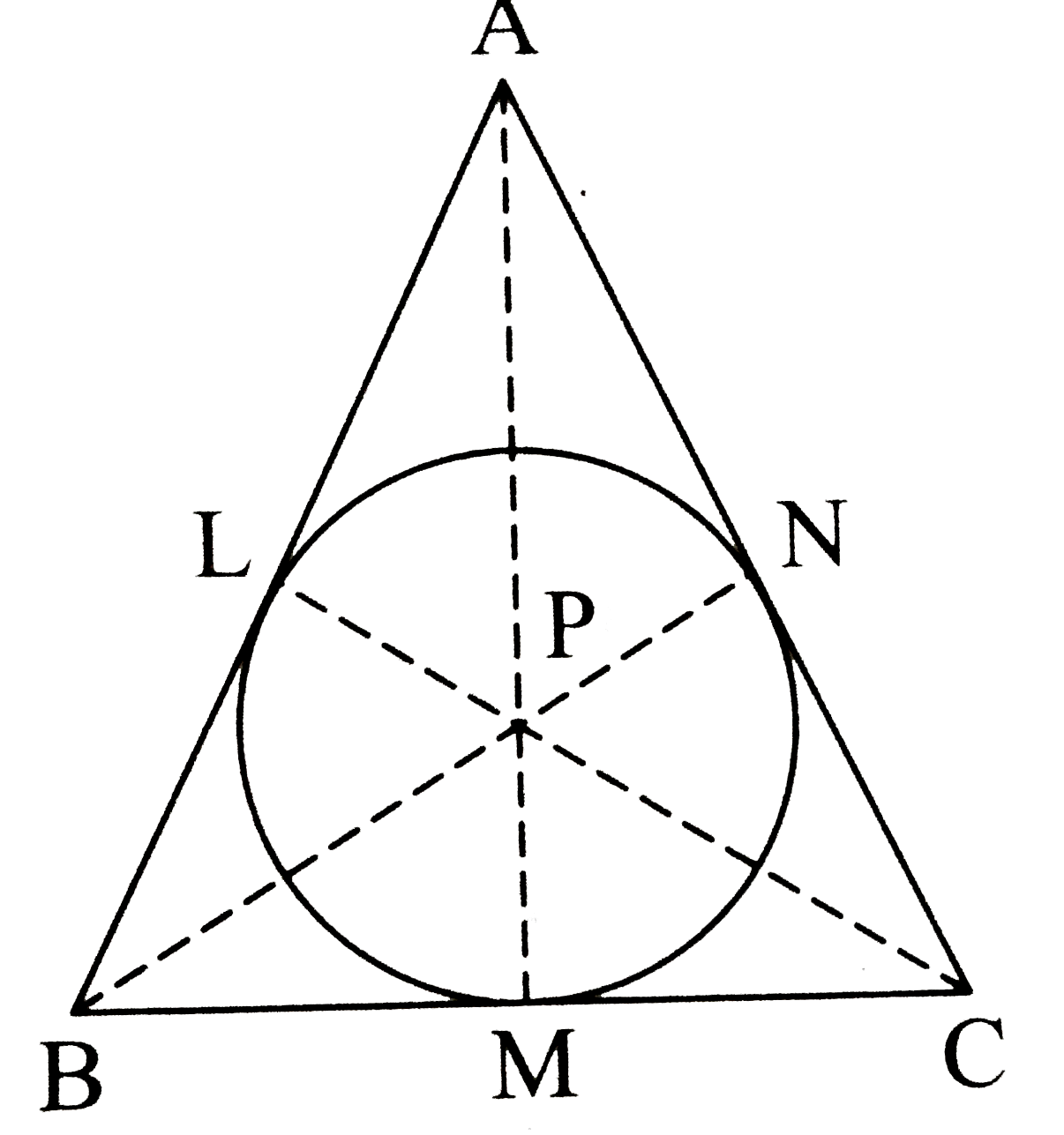
View SolutionA circle with centre P is inscribed in the △ ABC. Side AB, side BC and side AC touch the circle at points L,M and N respectively. Radius of the circle is r. Prove that: A(△ABC)=12(AB+BC+AC)×r.
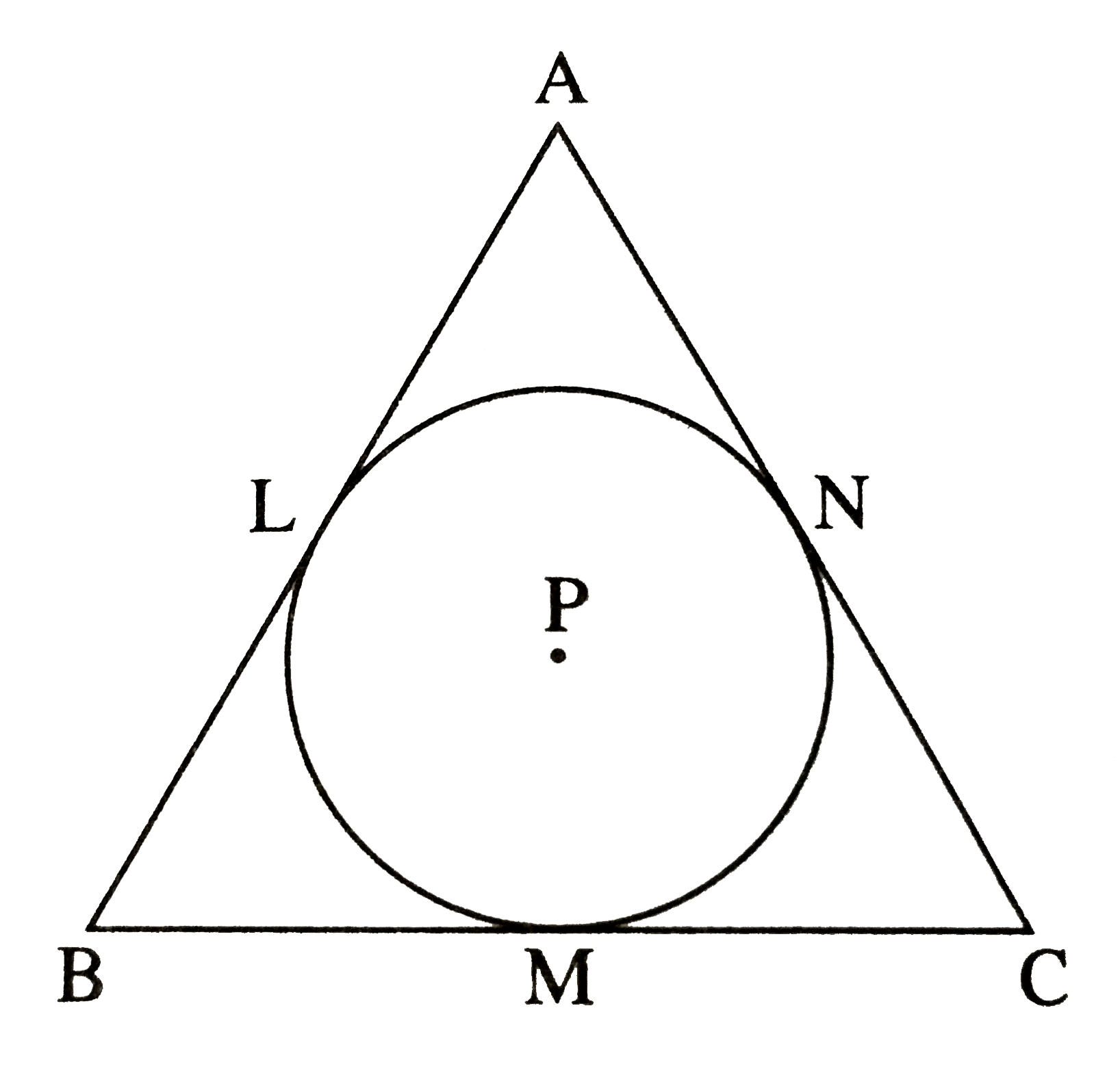
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionLet the incircle of ΔABC touches the sides BC, CA, AB at A1,B1,C1 respectively. The incircle of ΔA1B1C1 touches its sides of B1C1,C1A1andA1B1 at A2,B2,C2 respectively and so on.
Q. In ΔA4B4C4, the value of ∠A4 is:
View SolutionIf G1,G2 are centroids of triangles A1,B1,C1 and A2,B2,C2 respectively, then ¯¯¯¯¯¯¯¯¯A1A2+¯¯¯¯¯¯¯¯¯B1B2+¯¯¯¯¯¯¯¯¯C1C2=
View Solution
