Let ABC be a triangle such that ∠A=45∘,∠B=75∘, then a+c√2 is equal to
0
b
2b
−b
To solve the problem, we need to find the value of a+c√2 given the angles of triangle ABC where ∠A=45∘ and ∠B=75∘.
1. Find Angle C:
∠C=180∘−∠A−∠B
Substituting the known values:
∠C=180∘−45∘−75∘=60∘
2. Use the Sine Rule:
According to the sine rule:
asinA=bsinB=csinC=2R
Where R is the circumradius of triangle ABC.
3. Calculate Side a:
Using the sine rule for side a:
a=2RsinA=2Rsin45∘=2R⋅1√2=R√2
4. Calculate Side c:
Using the sine rule for side c:
c=2RsinC=2Rsin60∘=2R⋅√32=R√3
5. Substitute into the Expression:
Now we need to find a+c√2:
a+c√2=R√2+R√3√2
Simplifying:
=R√2+R√6=R(√2+√6)
6. Relate to Side b:
We also need to find side b:
b=2Rsin75∘
Using the sine addition formula:
sin75∘=sin(45∘+30∘)=sin45∘cos30∘+cos45∘sin30∘
Substituting the values:
=1√2⋅√32+1√2⋅12=√32√2+12√2=√3+12√2
Therefore,
b=2R⋅√3+12√2=R⋅√3+1√2
7. Final Expression:
Now we can express a+c√2 in terms of b:
a+c√2=R(√2+√6)=2b
Conclusion:
Thus, the value of a+c√2 is equal to 2b.
∠C=180∘−∠A−∠B
Substituting the known values:
∠C=180∘−45∘−75∘=60∘
According to the sine rule:
asinA=bsinB=csinC=2R
Where R is the circumradius of triangle ABC.
Using the sine rule for side a:
a=2RsinA=2Rsin45∘=2R⋅1√2=R√2
Using the sine rule for side c:
c=2RsinC=2Rsin60∘=2R⋅√32=R√3
Now we need to find a+c√2:
a+c√2=R√2+R√3√2
Simplifying:
=R√2+R√6=R(√2+√6)
We also need to find side b:
b=2Rsin75∘
Using the sine addition formula:
sin75∘=sin(45∘+30∘)=sin45∘cos30∘+cos45∘sin30∘
Substituting the values:
=1√2⋅√32+1√2⋅12=√32√2+12√2=√3+12√2
Therefore,
b=2R⋅√3+12√2=R⋅√3+1√2
Now we can express a+c√2 in terms of b:
a+c√2=R(√2+√6)=2b
Thus, the value of a+c√2 is equal to 2b.
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 2
19 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 3
33 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
Let ABC be a triangle such that ∠A=45∘,∠B=75∘, then a+c√2 is equal to
A2aB2a+1C3aD2a-1If in a ΔABC,∠A=45∘,∠B=75∘, then
Aa+c√3=2bBa+c=2bCa+c√2=2bDa−c=2bIn △ABC ,AB=AC , ∠B=40∘ Then ∠C is equal to
A50∘B40∘C80∘D140∘
In a ΔABC,∠A=65∘,∠C=75∘, where O is circumcentre , find ∠OAC.
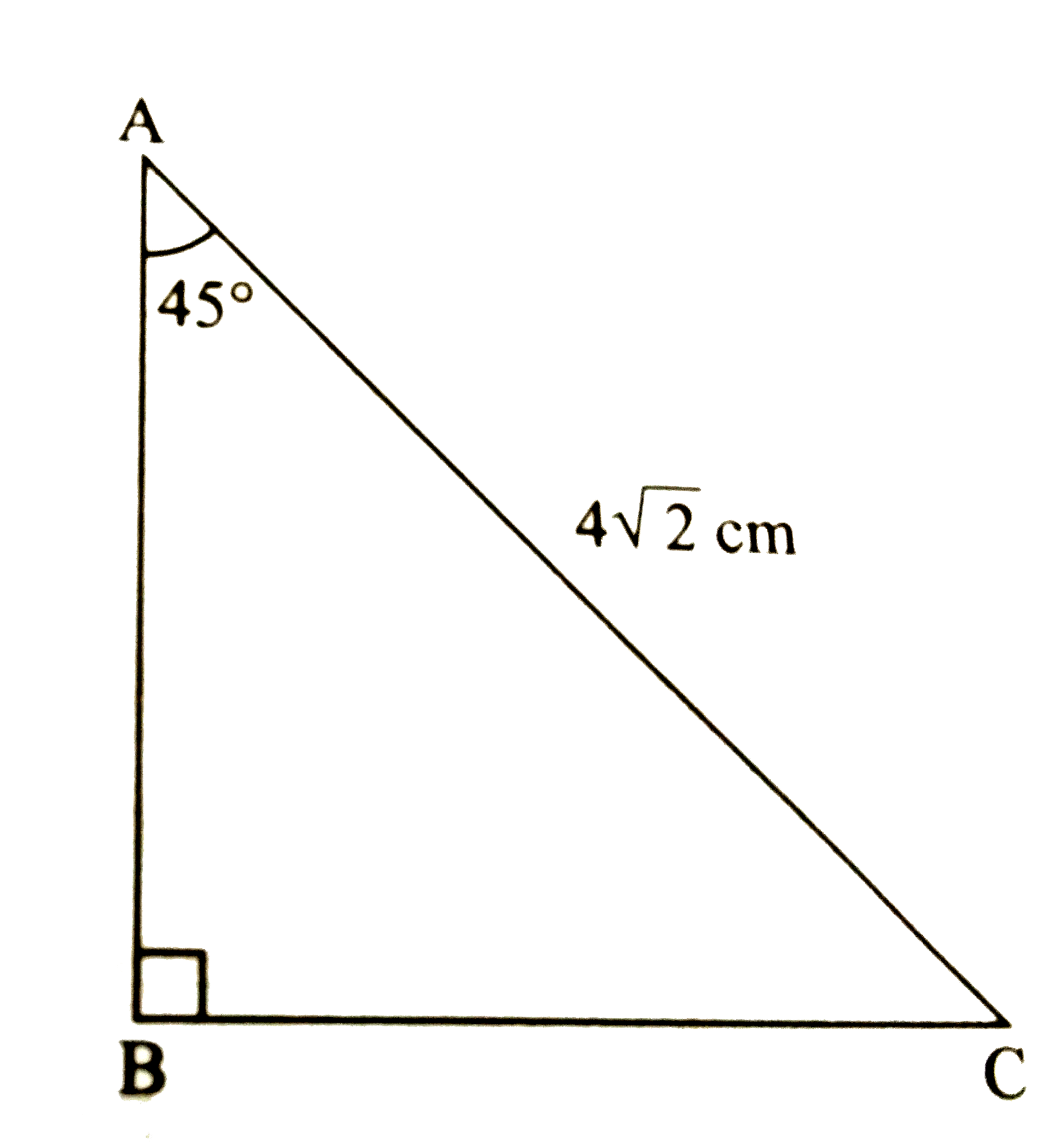
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionThe angles of a triangle ABC are in the ratio 3:5:4 then a+b+c√2=
View SolutionIn a triangle ABC, c = 2, A = 45∘, a = 2√2, than what is C equal to ?
View SolutionIn a ΔABC,∠C=3∠B=2(∠A+∠B), then ∠B = ?
View Solution
