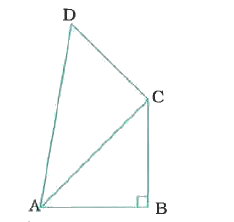
एक चतुर्भुज ABCD में, ∠B=90∘ तथा AD2=AB2+BC2+CD2 है, तो सिद्ध करो की ∠ACD=90∘|
Step by step video & image solution for एक चतुर्भुज ABCD में, angle B =90^(@) तथा AD^(2) =AB^(2) +BC^(2) +CD^(2) है, तो सिद्ध करो की angle ACD = 90^(@) | by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - अति लघुत्तरात्मक प्रश्न
17 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
45 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.6
25 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - बहु विकल्पीय प्रश्न
28 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - RD SHARMACHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - बहु विकल्पीय प्रश्न
16 Videos
Similar Questions
आधारभूत समानुपातिक्ता प्रमेय और उसके विलोम को प्रतिपादित कीजिए|
View Solutionएक 20 मीटर लम्बी ऊर्ध्वाधर छड़ की छाया की लम्बाई जमीन पर 10 मीटर लम्बी है | यदि उसी समय एक मीनार की छाया की लम्बाई 50 मीटर हो, तो मीनार की ऊँचाई है:
View Solutionनिम्न प्रश्न में ΔABC,ΔDEF के समरूप है
यदि ΔABC का क्षेत्रफल = 16 वर्ग सेमि,ΔDEF का क्षेत्रफल =25 वर्ग सेमि. तथा BC =2 .5सेमि, हो तो EF ज्ञात कीजिए|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View SolutionIn a quadrilateral ABCD, ∠B=90∘andAD2=AB2+BC2+CD2 prove that ∠ACD=90∘ .
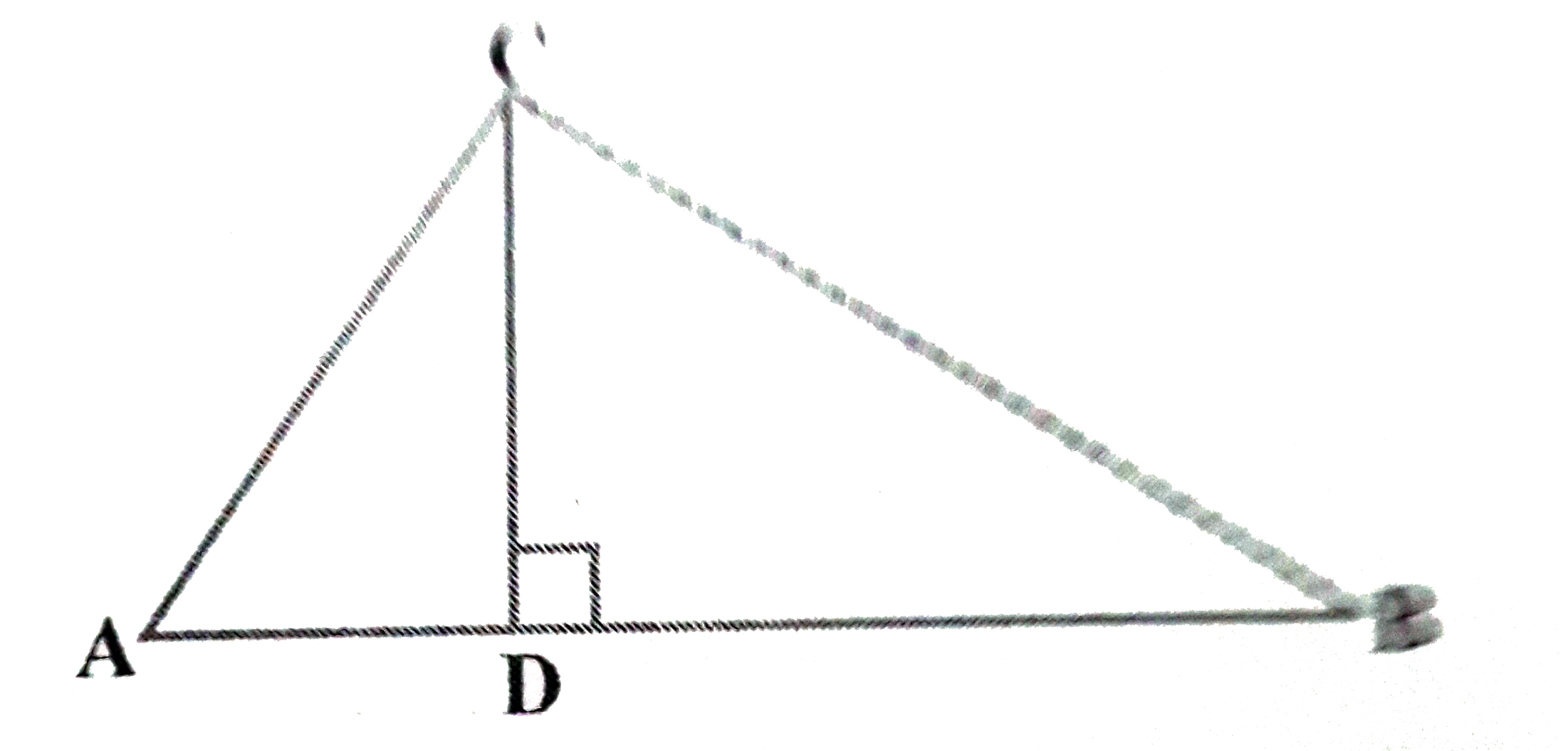
View Solutionआकृति 6.48 में ∠ACB=90∘ तथा CD⊥AB है। सिद्ध कीजिए की BC2AC2=BDAD है
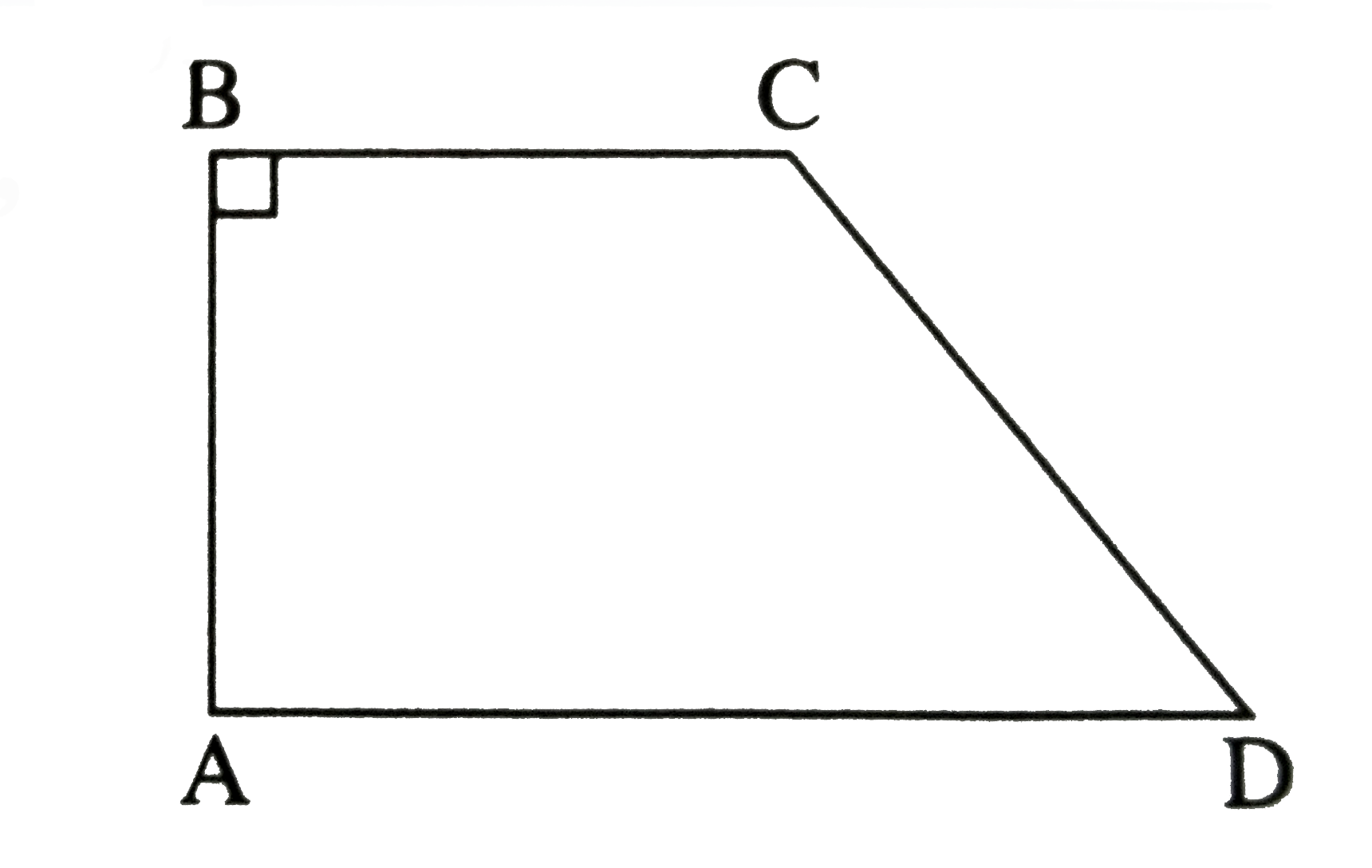
View Solutionएक चतुर्भुज ABCD में, ∠B=90∘ है यदि AD2=AB2+BC2+CD2 हो तो सिद्ध कीजिए कि ∠ACD=90∘
View SolutionIn the figure ∠B=90∘,
AD2=AB2+BC2+CD2.
Prove ∠ACD=90∘ .
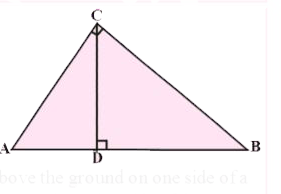
View SolutionIn ∠ACD=90∘andCD⊥AB. Prove that BC2AC2=BDAD
View SolutionIn ΔACB,∠C=90∘ and CD⊥ AB
Prove that BC2AC2=BDAD.
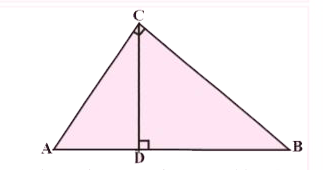
View SolutionIn ΔACB,∠C=90∘ and CD⊥ AB
Prove that BC2AC2=BDAD.
View SolutionIn a quadrilateral ABCD, ⌊B=90∘. If AD2=AB2+BC2+CD2, prove that ⌊ACD=90∘.
View SolutionIn a quadrilateral ABCD, ∠B=90∘ and AD2=AB2+BC2+CD2. Prove that ∠ACD=90∘.
View SolutionIn a quadrilateral ABCD, ∠B=90∘and∠D=90∘. Prove that :
2AC2−AB2=BC2+CD2+DA2
View SolutionIn a quadrilateral ABCD ∠B=∠D=90∘ Prove that : 2AC2−BC2=AB2+AD2+DC2
View Solution
