In a quadrilateral ABCD, ∠B=90∘andAD2=AB2+BC2+CD2 prove that ∠ACD=90∘ .
To prove that ∠ACD=90∘ in quadrilateral ABCD where ∠B=90∘ and AD2=AB2+BC2+CD2, we can follow these steps:
1. Identify the Given Information:
- We know that ∠B=90∘.
- We also have the equation AD2=AB2+BC2+CD2.
2. Apply the Pythagorean Theorem in Triangle ABC:
- Since ∠B=90∘, we can apply the Pythagorean theorem to triangle ABC.
- According to the theorem, we have:
AC2=AB2+BC2
3. Substitute AC2 into the Given Equation:
- We know from the given information that:
AD2=AB2+BC2+CD2
- From step 2, we can substitute AC2 into the equation:
AD2=AC2+CD2
4. Equate the Two Expressions for AD2:
- Now we have two expressions for AD2:
AD2=AC2+CD2
AD2=AB2+BC2+CD2
- Since both expressions are equal to AD2, we can set them equal to each other:
AC2+CD2=AB2+BC2+CD2
5. Simplify the Equation:
- By subtracting CD2 from both sides, we get:
AC2=AB2+BC2
6. Apply the Pythagorean Theorem Again:
- The equation AC2=AB2+BC2 confirms that triangle ABC is a right triangle at B.
- This means that ∠ACB=90∘.
7. Conclude the Proof:
- Since we have established that AC2=AB2+BC2 and AD2=AC2+CD2, we can conclude that triangle ACD must also be a right triangle at C.
- Therefore, ∠ACD=90∘.
Final Statement:
Thus, we have proven that ∠ACD=90∘.
---
- We know that ∠B=90∘.
- We also have the equation AD2=AB2+BC2+CD2.
- Since ∠B=90∘, we can apply the Pythagorean theorem to triangle ABC.
- According to the theorem, we have:
AC2=AB2+BC2
- We know from the given information that:
AD2=AB2+BC2+CD2
- From step 2, we can substitute AC2 into the equation:
AD2=AC2+CD2
- Now we have two expressions for AD2:
AD2=AC2+CD2
AD2=AB2+BC2+CD2
- Since both expressions are equal to AD2, we can set them equal to each other:
AC2+CD2=AB2+BC2+CD2
- By subtracting CD2 from both sides, we get:
AC2=AB2+BC2
- The equation AC2=AB2+BC2 confirms that triangle ABC is a right triangle at B.
- This means that ∠ACB=90∘.
- Since we have established that AC2=AB2+BC2 and AD2=AC2+CD2, we can conclude that triangle ACD must also be a right triangle at C.
- Therefore, ∠ACD=90∘.
Thus, we have proven that ∠ACD=90∘.
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Revision Exercise Very Short Questions
Explore 9 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Revision Exercise Short Questions
Explore 10 Videos
- TRIANGLES Book:NAGEEN PRAKASHANChapter:TRIANGLES Exercise:Exercise 6c
Explore 11 Videos
- STATISTICS Book:NAGEEN PRAKASHANChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHANChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
In a quadrilateral ABCD, ∠B=90o . If AD2=AB2+BC2+CD2 then prove that ∠ACD=90o .
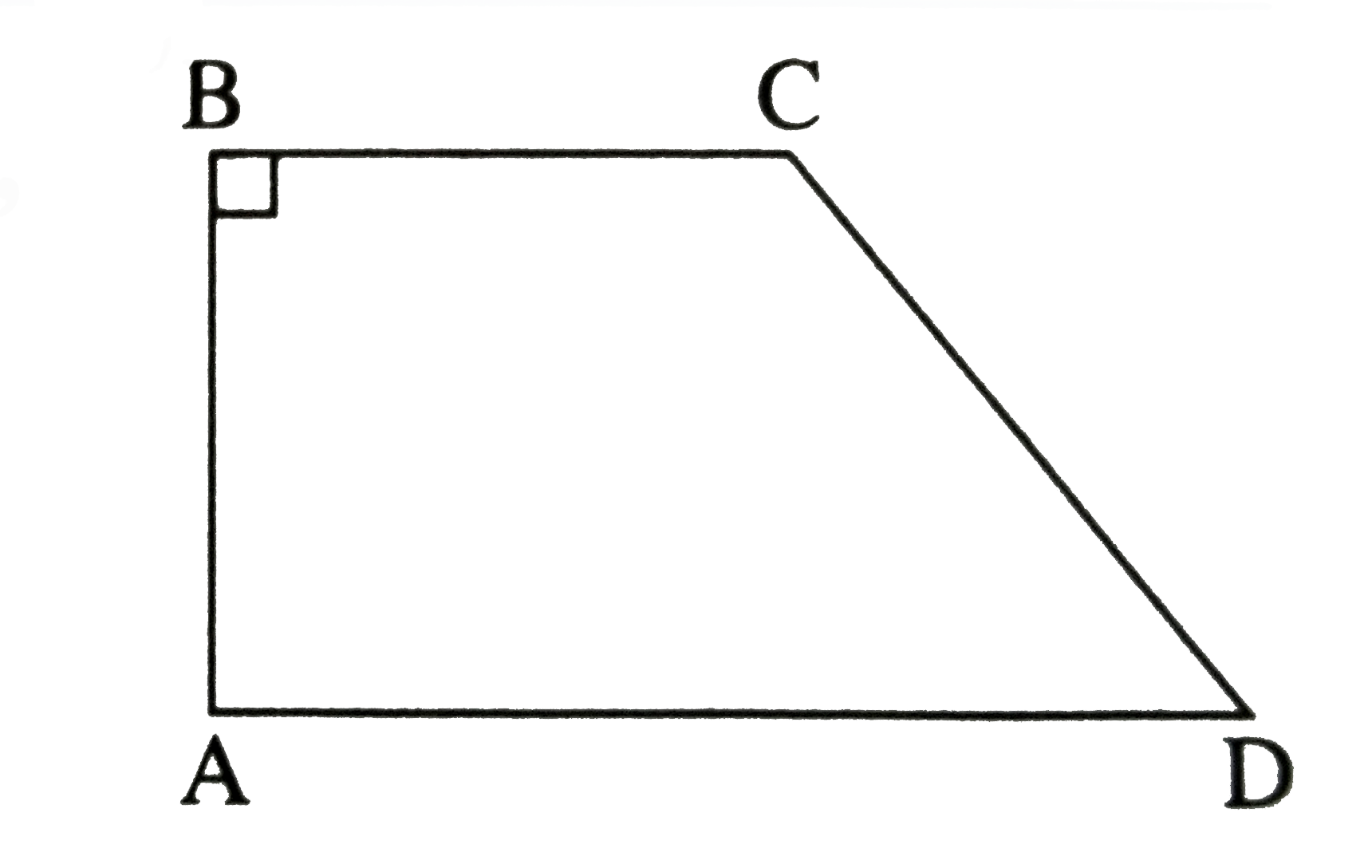
View SolutionIn the figure ∠B=90∘,
AD2=AB2+BC2+CD2.
Prove ∠ACD=90∘ .
View SolutionIn a quadrilateral ABCD , ∠B=90o , AD2=AB2+BC2+CD2 , prove that ∠ACD=90o
View SolutionIn a quadrilateral ABCD, ∠A+∠D=90∘. Prove that
AC2+BD2=AD2+BC2
View SolutionIn a quadrilateral ABCD, ∠A+∠D=90∘. Prove that AC2+BD2=AD2+BC2.
View SolutionIn a ΔABC,∠B=90∘andAC=8√2. If AB=BC, then find AB.
View SolutionIn a quadrilateral ABCD, show that (AB+BC+CD+DA)<2(BD+AC).
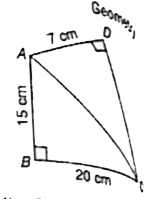
View SolutionIn the given quadrilateral ABCD,AB=15cm,BC=20cmandAD=7cm∠ABC=∠ADC=90∘. Find the length of side CD:
View SolutionIn a quadrilateral ABCD, prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2, where P and Q are middle points of diagonals AC and BD.
View SolutionIn a quadrilateral ABCD prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2 where P and Q are middle points of diagonals AC and BD.
View Solution