मान लीजिए कि केंद्र O तथा Q वाले दो व्रतों का एक प्रतिच्छेद बिंदु A है । दोनों व्रतों की बिंदु A पर स्पर्श रेखाएँ व्रतों को क्रमशः फिर से B तथा C पर मिलती हैं । मान लीजिए बिंदु P इस प्रकार खोजा गया है कि AOPQ एक समान्तर चतुर्भुज है । सिद्ध कीजिए कि P त्रिभुज ABC का परिकेन्द्र है ।
यह सिद्ध करने के लिए कि बिंदु P त्रिभुज ABC का परिकेन्द्र है , यह दर्शाना पर्याप्त होगा कि त्रिभुज ABC की भुजाओं के लम्ब समद्विभाजकों का प्रतिच्छेदन बिंदु P है अर्थात भुजाओं AB और AC के लम्ब समद्विभाजक क्रमशः OP और PQ हैं ।

चूँकि O केंद्र वाले वृत्त के बिंदु A पर AC स्पर्श रेखा है तथा OA वृत्त की त्रिज्या है।
एक समान्तर चतुर्भुज है ]
की लम्ब समद्विभाजन है। " " वृत्त का केंद्र है ]
चूँकि Q केंद्र वाले वृत्त के बिंदु A पर BA स्पर्श रेखा है तथा AQ वृत्त की त्रिज्या है।
एक समान्तर चतुर्भुज है
की लम्ब समद्विभाजन है।
अतः भुजाओं AC और AB के लम्ब समद्विभाजक क्रमशः PQ और PO हैं और इनका प्रतिच्छेद बिंदु P है। अतः का परिकेन्द्र P है|
Topper's Solved these Questions
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.1
4 Videos
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.2
22 Videos
- वास्तविक संख्याएँ BOOK - RD SHARMACHAPTER - वास्तविक संख्याएँ EXERCISE - बहु विकल्पीय प्रश्न
25 Videos
- वृत्तों से सम्बन्धित क्षेत्रफल BOOK - RD SHARMACHAPTER - वृत्तों से सम्बन्धित क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
45 Videos
Similar Questions
रिक्त स्थानों की पूर्ति कीजिए :
(i) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को कहते ………. हैं।
(ii) एक वृत्त की ..... समानान्तर स्पर्श रेखाएँ हो सकती हैं ।
(iii) किसी वृत्त की स्पर्श रेखा उसे ..... बिंदुओं पर प्रतिच्छेद करती है ।
(iv) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को कहते हैं ।
(v) वृत्त पर स्पर्श रेखा के स्पर्श बिन्दु तथा उस बिन्दु से गुजरने वाली त्रिज्या के बीच का कोण ...... का होता है ।
View Solutionयदि किसी वृत्त C(O,r) पर PT स्पर्श रेखा है तथा OP=17 सेमी और OT =8 सेमी हो , तो स्पर्श रेखा की लम्बाई ज्ञात करो ।
View Solution144 के अभाज्य गुणनखण्डों में 2 की घात है :
View Solutionएक वृत्त की परिधि तथा क्षेत्रफल रूप से समान हों, तो वृत्त का व्यास है :
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
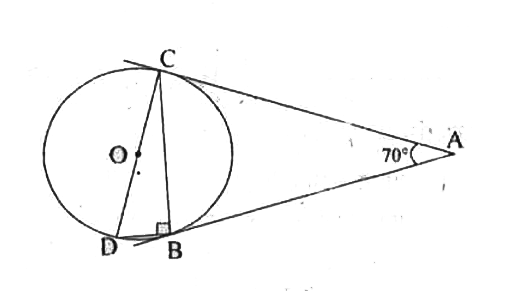
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
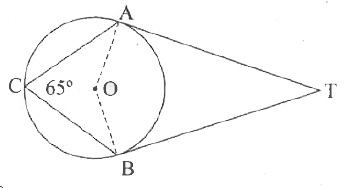
View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -

View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionस्पर्श रेखा #!#व्रतों का निकाय
View Solutionव्रतों का निकाय #!#जीवा #!#उभयनिष्ट स्पर्श रेखाएं
View Solutionकिसी बिंदु पर स्पर्श रेखा तथा अभिलंब का समीकरण
View Solution
