The circles shown in the given figure are called externally touching circles. Why?
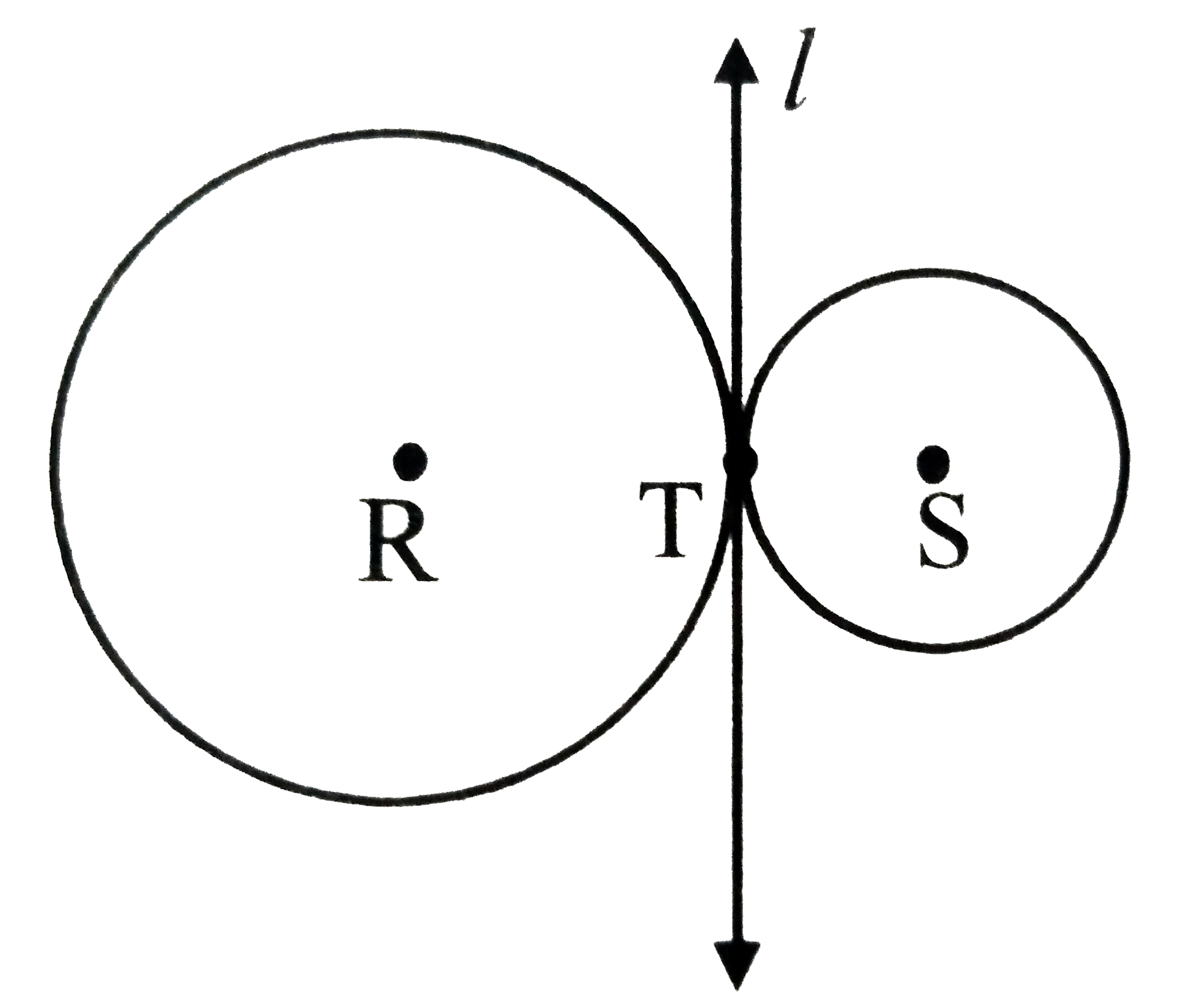
The correct Answer is:Hence the given circles are externally touching circles
Step by step video & image solution for The circles shown in the given figure are called externally touching circles. Why? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.14videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.25videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Lets recall1videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
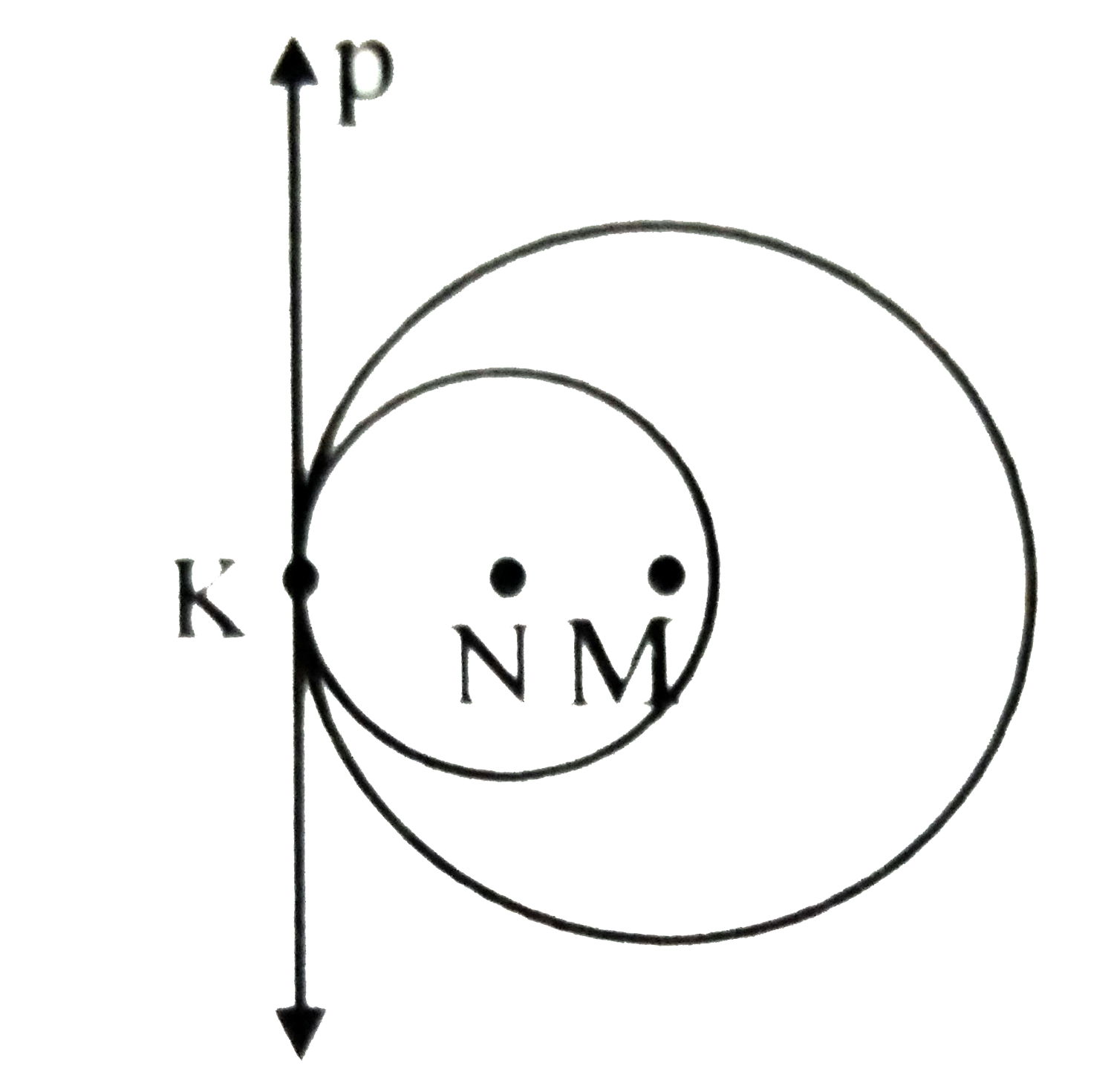
The circles shown in the given figure are called internally touching circles. Why?
 View Solution
View SolutionIf the chord of contact of tangents from a point P to a given circle passes through Q, then the circle on PQ as diameter. cuts the given circle orthogonally touches the given circle externally touches the given circle internally none of these
View Solution
Knowledge Check
- Question 1 - Select One
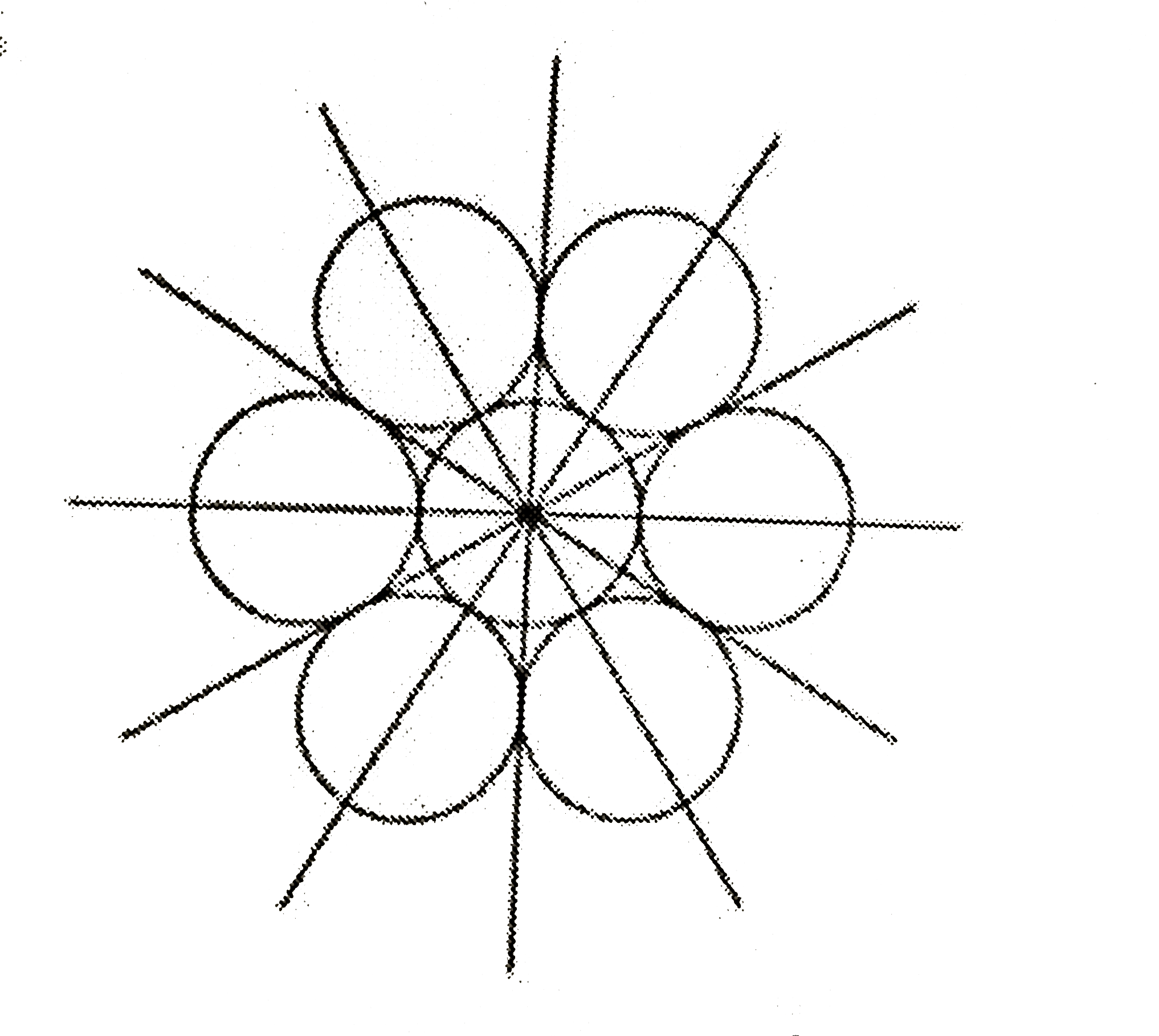
In the given figure, the radii of the circles are equal. The middle circle is touching all the other circles and each of the other circles is touching exactly three circles as shown in the figure. What is the total number of lines of symmetry that can be drawn for the given figure?A3B6C12DInfinitely many - Question 2 - Select One
Variable circles are drawn touching two fixed circles externally then locus of centre of variable circle is
AparabolaBellipseChyperbolaDcircle - Question 3 - Select One
The locus of the centre of a circle, which touches externally to the circle x2+y2−6x−6y+14=0 and also touches the y-axis, is given by
Ax2−y2−10y+14=0Bx2−10x−6y+14=0Cy2−6x−10y+14=0Dy2−10x−6y+14=0
PA and PB are tangents to the circle with centre O from an external point P, touching the circle at A and B respectively. Show that the quadrilateral AOBP is cyclic.
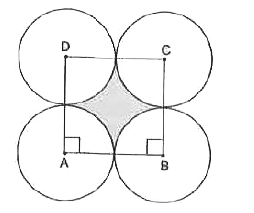
View SolutionIn the given figure, four equal circles are described about corners of a square so that each circle touches two of the circles as shown in the figure. Find the area of the shaded region, each side of the square measuring 14 cm.
 View Solution
View SolutionIn the adjoining figure , line PQ is a common tangent to the externally touching circles and the radii of two circles are 25cm and 9cm. Find the length of the common tangent segment of these circles.
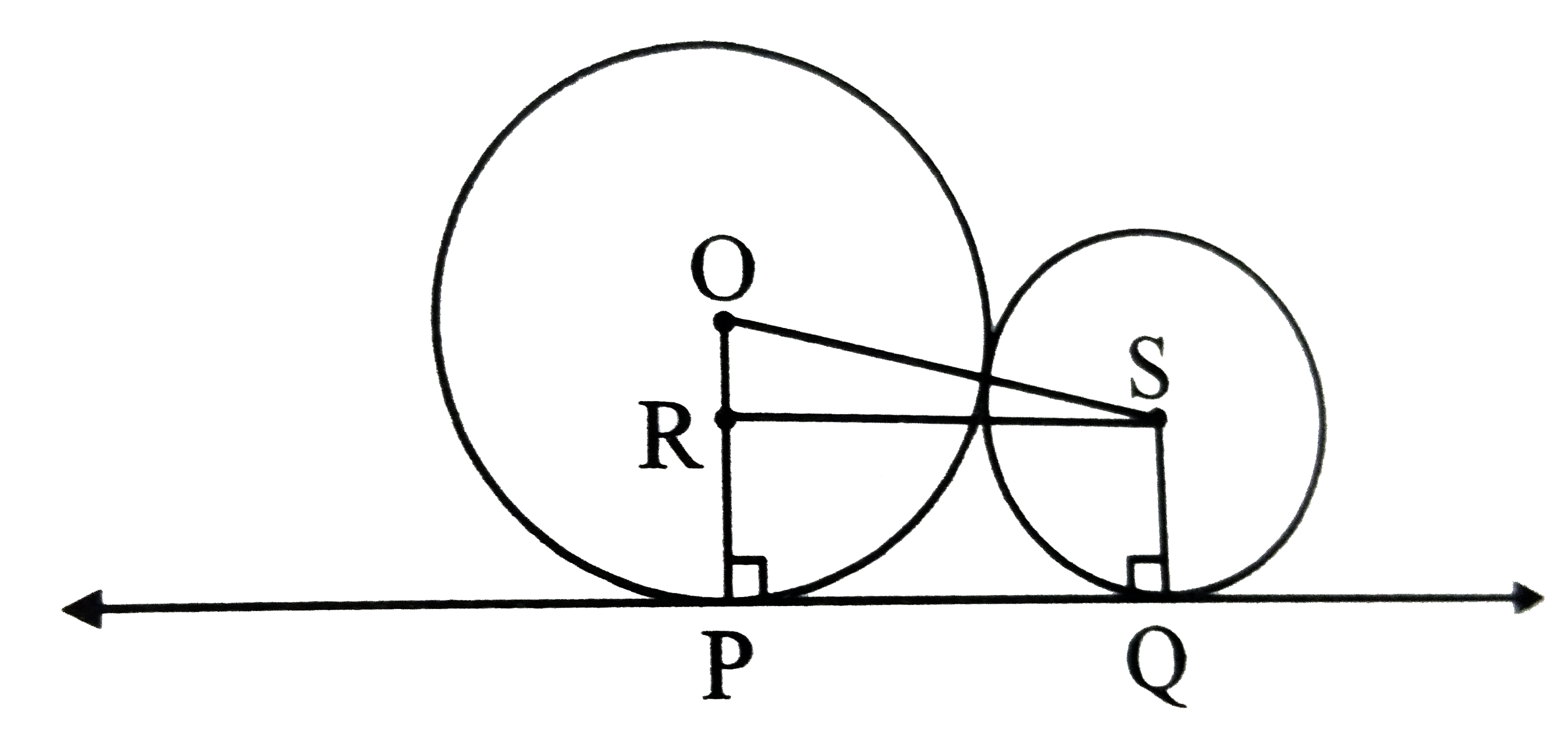 View Solution
View SolutionThe locus of the centre of a circle, which touches externally the circle x2+y2−6x−6y+14=0 and also touches the y-axis, is given by the equation
View SolutionThe locus of the centre of a circle, which touches externally the circle x2+y2−6x−6y+14=0 and also touches the y-axis, is given by the equation
View Solution

