If the chord of contact of tangents from a point P to a given circle passes through Q, then the circle on PQ as diameter. cuts the given circle orthogonally touches the given circle externally touches the given circle internally none of these
Step by step video & image solution for If the chord of contact of tangents from a point P to a given circle passes through Q , then the circle on P Q as diameter. cuts the given circle orthogonally touches the given circle externally touches the given circle internally none of these by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If the chord of contact of tangents from a point P to a given circle passes through Q, then the circle on PQ as diameter. cuts the given circle orthogonally touches the given circle externally touches the given circle internally none of these
View SolutionIf the chord of contact of tangents from a point P to a given circle passes through Q, then the circle on PQ as diameter. cuts the given circle orthogonally touches the given circle externally touches the given circle internally none of these
View Solution
Knowledge Check
The locus of the centre of a circle the touches the given circle externally is a _______
AcurveBstraight lineCcircleDhelixThe locus of the centre of the circle that touch a given circle internally is ________
Astraight lineBhellixCcircleDNone of theseIf the chord of contact of tangents from a point P(h, k) to the circle x2+y2=a2 touches the circle x2+(y−a)2=a2, then locus of P is
Ay2=a2−2axBy2=a2+2axCx2=a2+2ayDx2=a2−2ay
If PandQ a be a pair of conjugate points with respect to a circle S. Prove that the circle on PQ as diameter cuts the circle S orthogonally.
View SolutionThe circles shown in the given figure are called externally touching circles. Why?
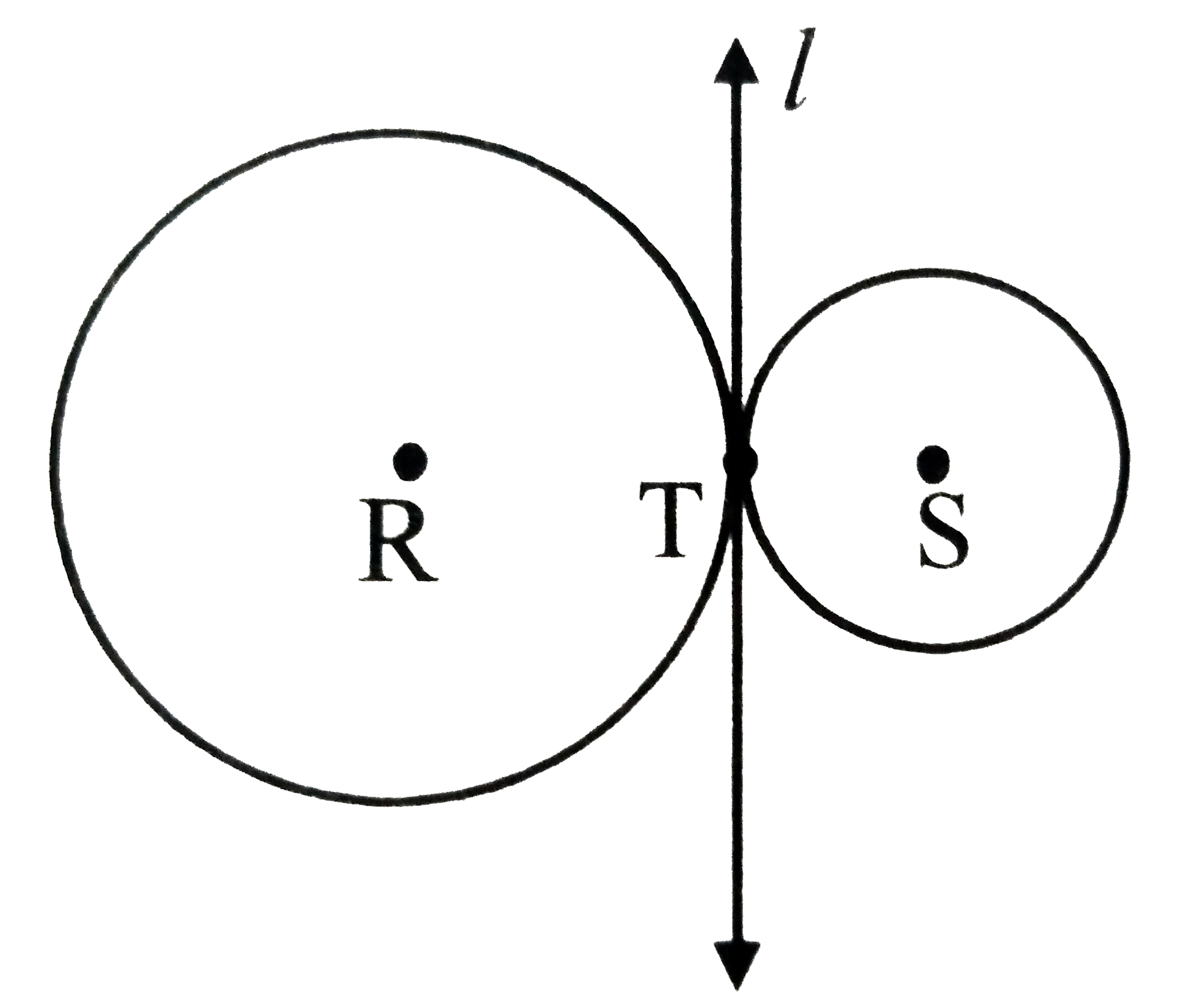
View SolutionThe circles shown in the given figure are called internally touching circles. Why?
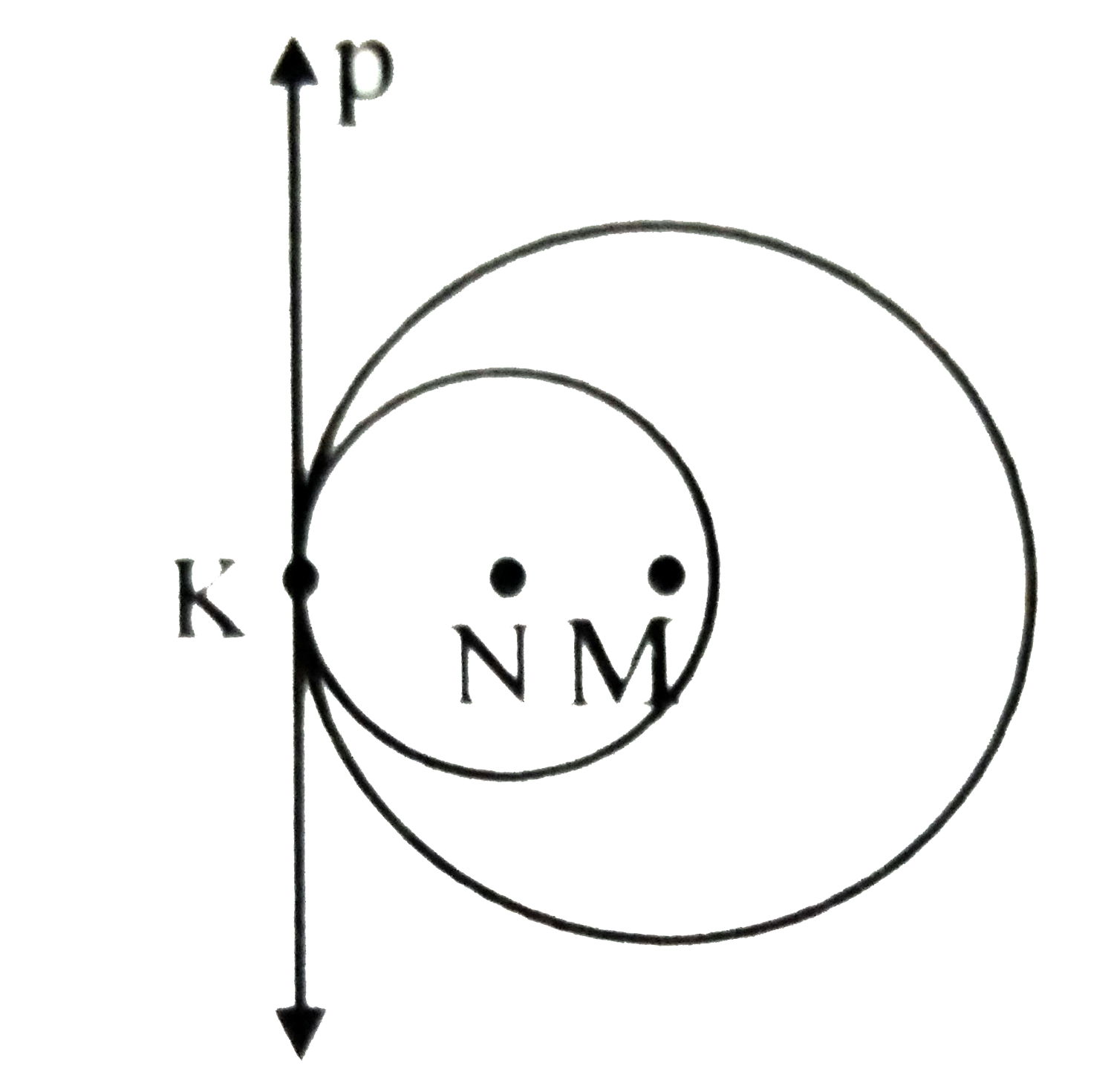
View SolutionIf the circle passes through the point (a,b) and cuts the circle x2+y2=k2 orthogonally, then the locus of its centre is given by :
View SolutionThe chord of contact of tangents from three points P, Q, R to the circle x2+y2=c2 are concurrent, then P, Q, R
View Solution
