Point O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

Step by step video & image solution for Point O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment
9 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question
25 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics
4 Videos
- CO-ORDINATE GEOMETRYBOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT
19 Videos
Similar Questions
Knowledge Check
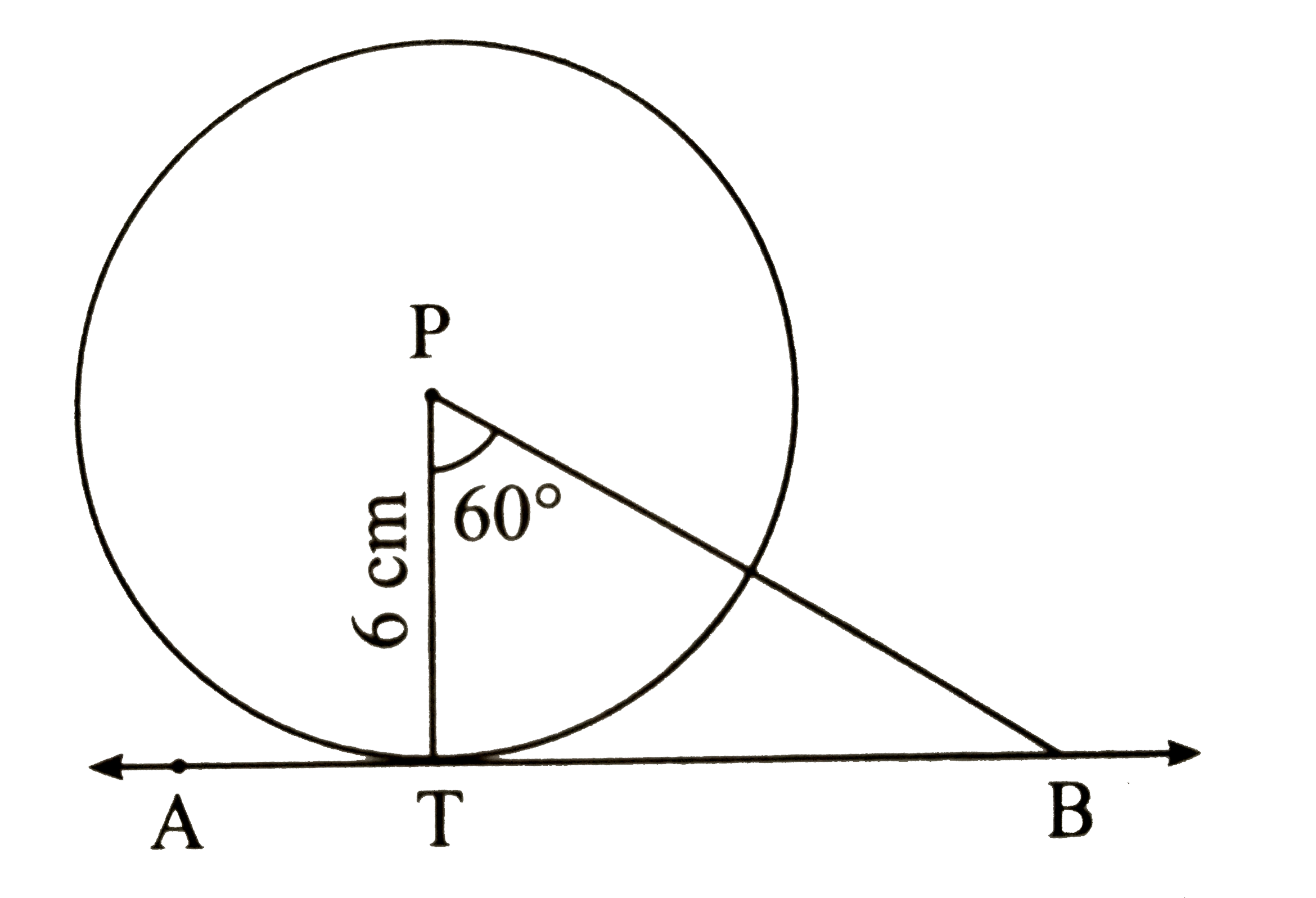
From a point P which is at a distance of 10 cm from the centre O of a circle of radius 6 cm, a pair of tangents PQ and PR to the circle at point Q and P respectively, are drawn. Then the area of the quadrilateral PQOR is equal to
A30 sq.cmB40 sq.cmC24 sq.cmD48 sq.cmA line meets the coordinate axes at A and B. A circle is circumscribed obout the triangle OAB. If the distance of the points A and B from the tangent at O, the origin, to the circle are m and n respectively, find the diameter of the circle.
A2m+n2B(m+n)Cmnm+nDm+2n2
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
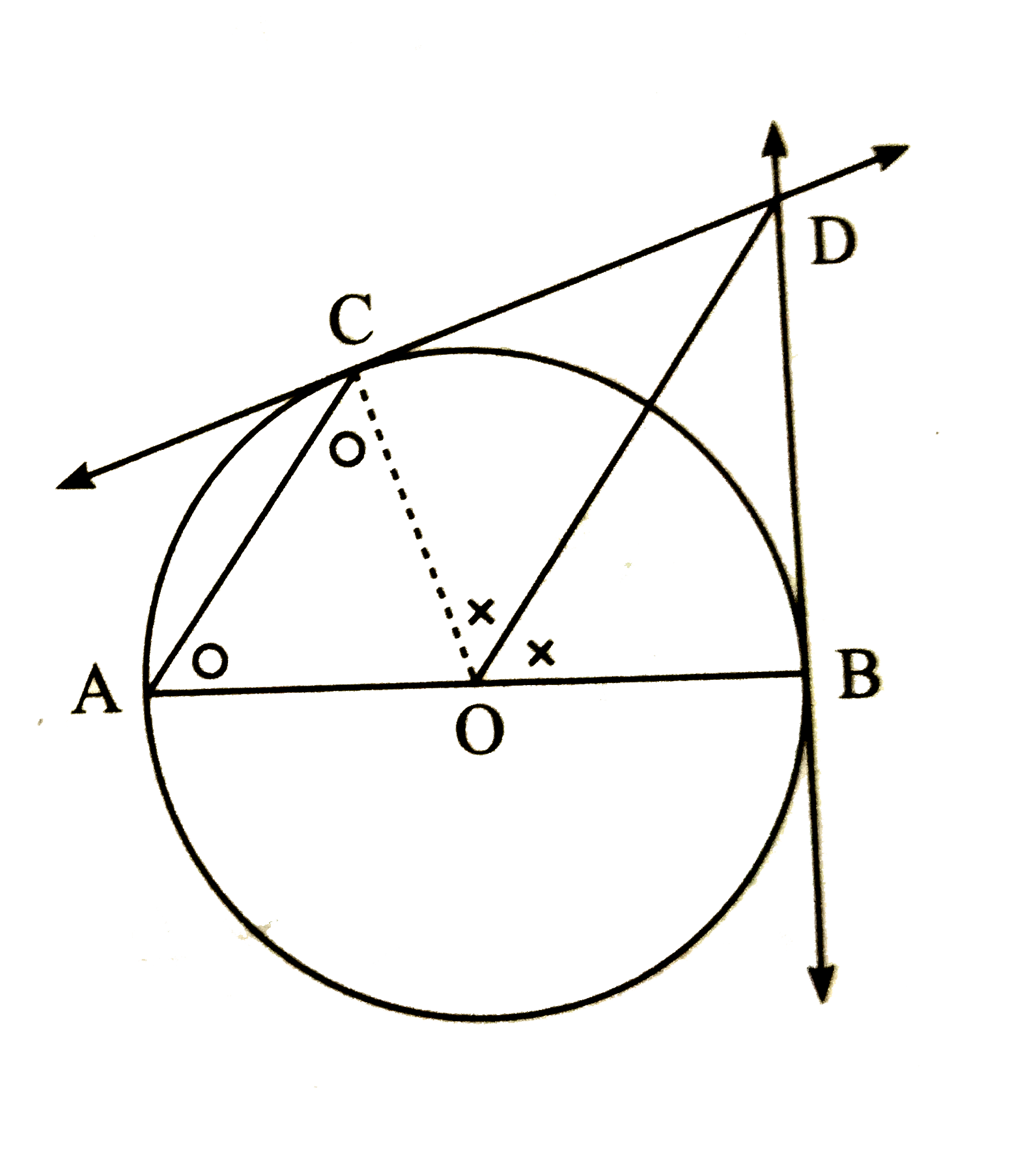
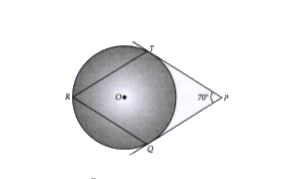
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
View Solution
P, Q are the points on the circle. The part of the circle, PQ is called ________ of the circle.
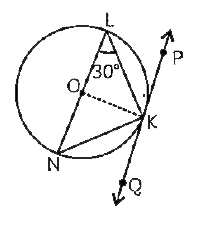
View SolutionIn the figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.
View Solution
If A, B are the point on the circle. The line segment ¯¯¯¯¯¯AB is called _______ of the circle.
View Solution