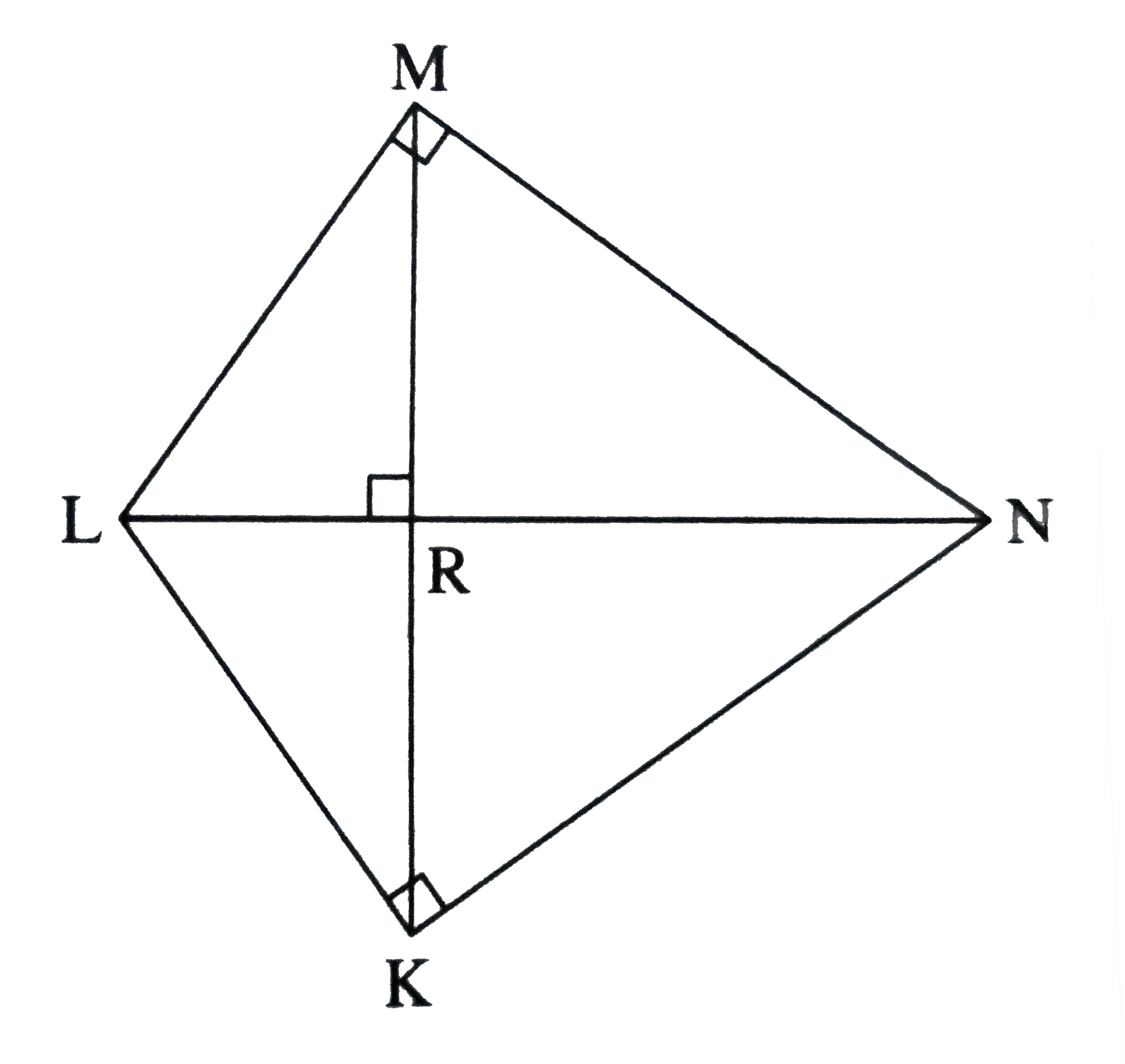
In the figure , ∠LMN=∠LKN=90∘
seg MK ⊥ seg LN .
Complete the following activtiy
to prove R is the midpoint of seg MK .
Step by step video & image solution for In the figure , angle LMN = angle LKN = 90^(@) seg MK bot seg LN . Complete the following activtiy to prove R is the midpoint of seg MK . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 3 MARK QUESTIONS )
8 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 2 MARK QUESTIONS )
2 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 1 MARK MULTIPLE CHOICE QUESTIONS )
11 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.4
12 Videos
- QUADRATIC EQUATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATION EXERCISE - CHALLENGIN QUESTIONS
2 Videos
Similar Questions
In the figure, ∠LMN=∠LKN=90∘
seg MK⊥ seg LN.
Complete the following activity to prove R is the midpoint of seg MK.
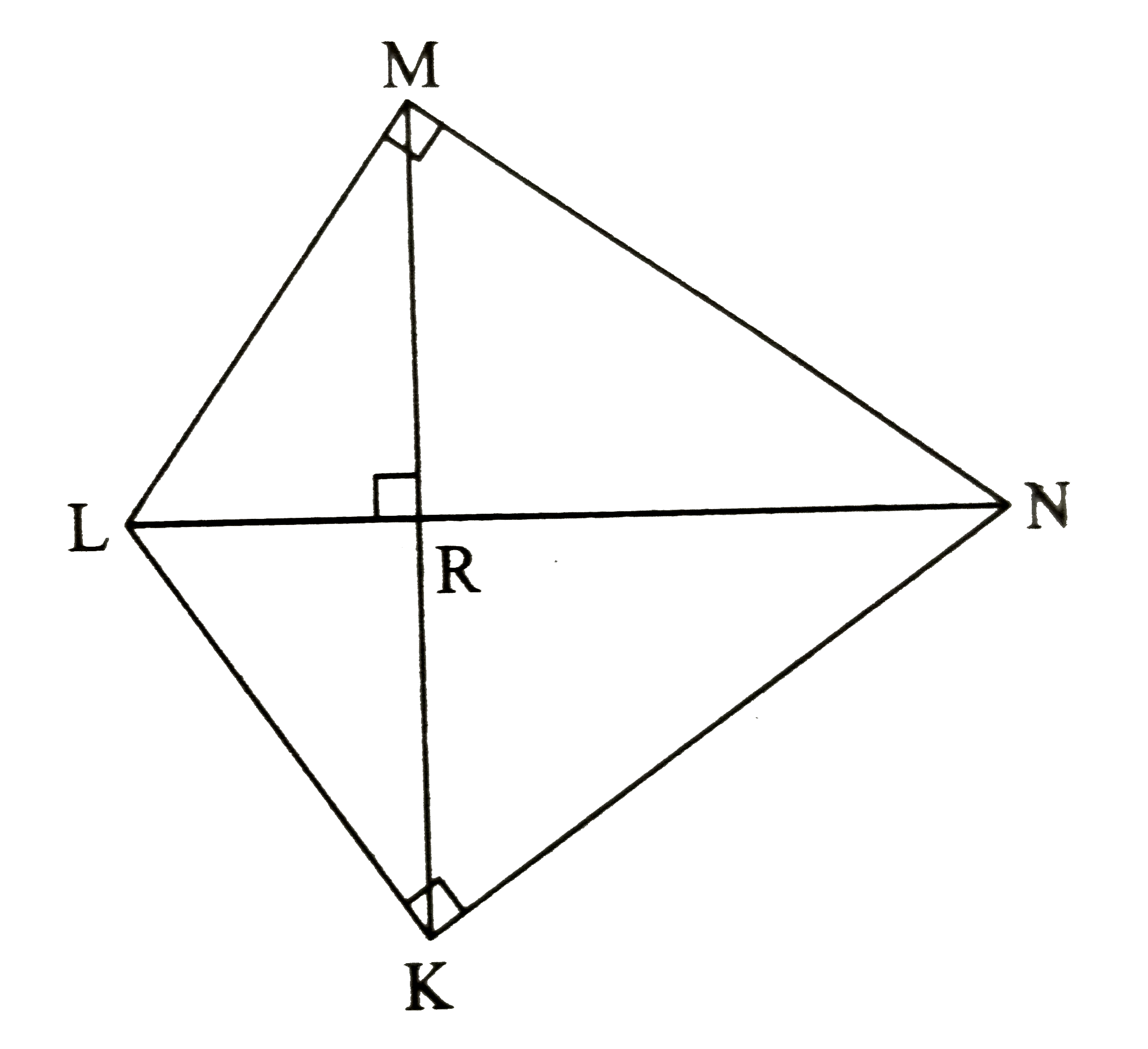
Proof: In ΔLMN, ∠LMN=90∘
seg MR⊥ hypotenuse LN
∴ by property of geometric mean,
MR2=□×RN
In ΔLKN, ∠LKN=90∘
seg KR⊥ hypotenuse LN
∴ by property of geometric mean,
KR2=LR×□
From (1) and (2), we get
MR2=□∴MR=□.
∴R is the midpoint of seg MK.
View SolutionIn the figure, ∠DFE=90∘, seg FG⊥ side DE, DG=8, FG=12 then complete the following activity to find the length of seg DE.
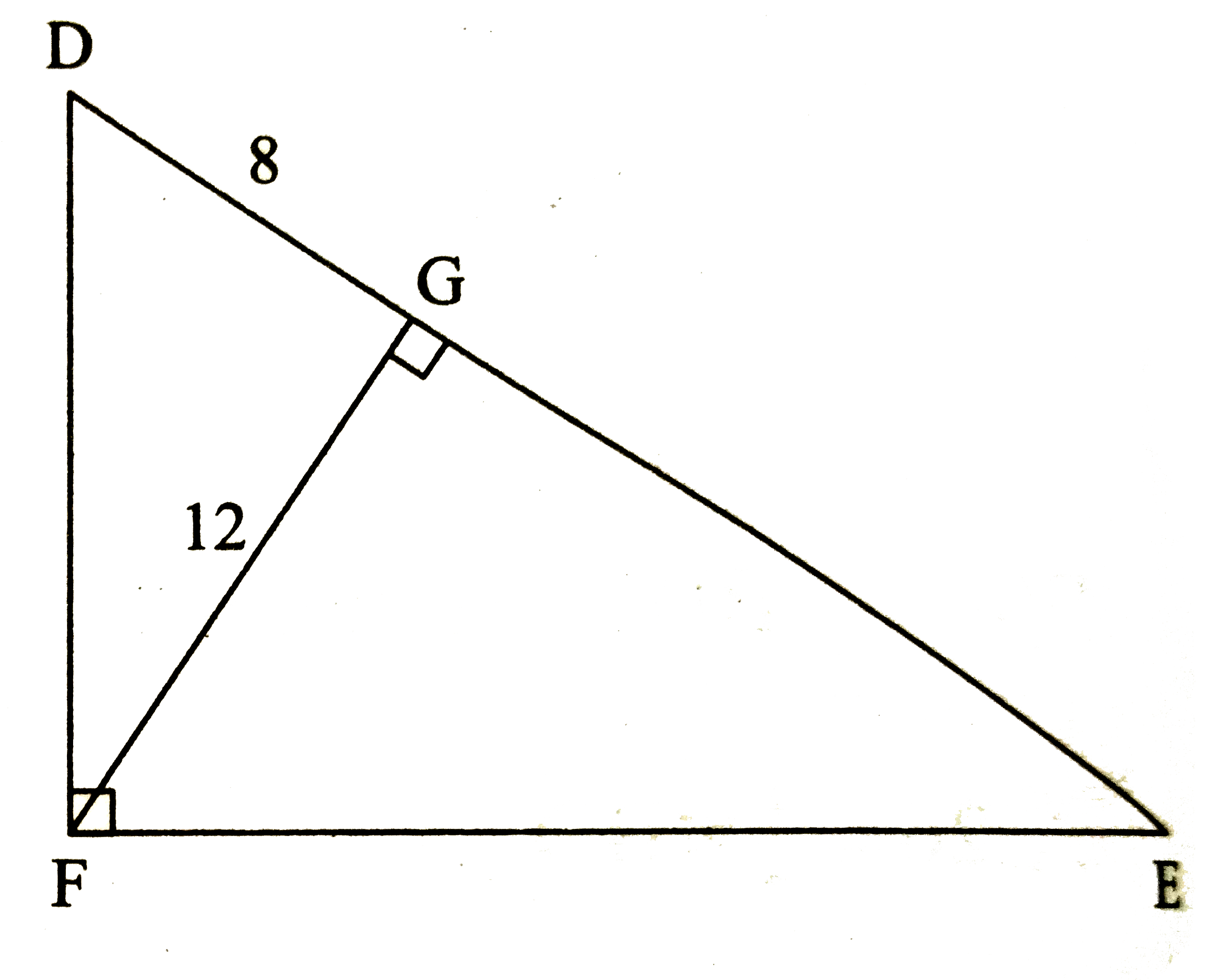
In ΔDFE, ∠DFE=90∘,
seg FG⊥ hypotenuse DE
∴ by theorem of geometric mean,
FG2=□×EG
∴122=□×EG
EG=12×12□
∴EG=□
DE=DG+GE=8+□=□
View SolutionIn the given figure, ∠PQR=90∘, seg QN⊥segPR,PN=9,NR=16.Find QN.
View Solution(A) Complete any two out of three activites :
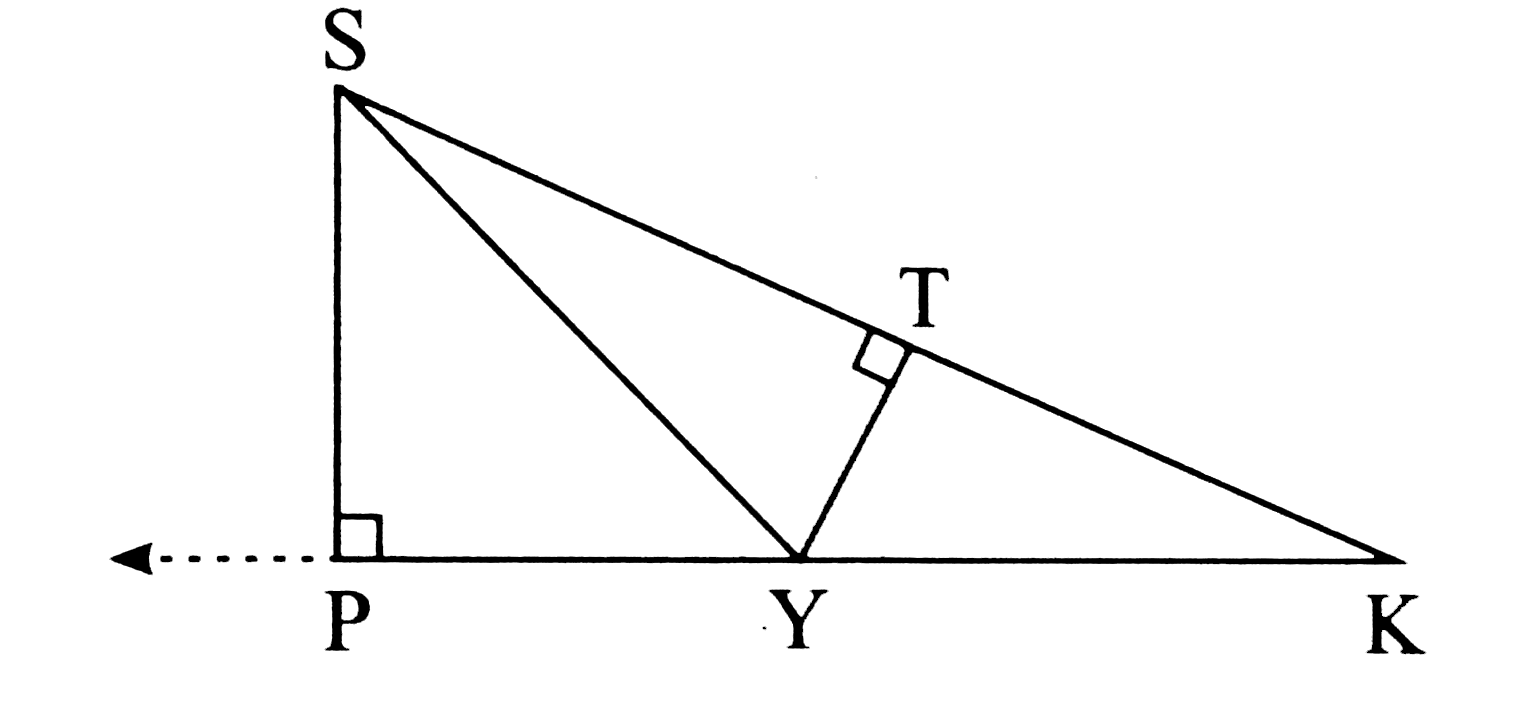 In the figure , seg SP ⊥ side YK . Seg YT⊥ side SK . If SP = 6 , YK = 13, YT = 5 and TK = 12 then complete the following activity to find A(ΔSYK):A(ΔYTK)
In the figure , seg SP ⊥ side YK . Seg YT⊥ side SK . If SP = 6 , YK = 13, YT = 5 and TK = 12 then complete the following activity to find A(ΔSYK):A(ΔYTK)
The ratio of the areas of the two Deltas is equal to the ratio of the products of their □ and the corresponding heights
∴A(ΔSYK)A(ΔYTK)=□×SPTK×TY
=13×612×□
=□□
View SolutionIn the adjoining figure.
∠QPR=90∘,
seg PM⊥segQRandQ−M−R,PM=10,QM=8, find QR.
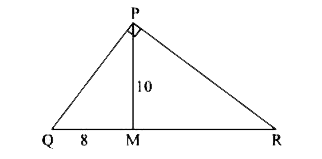
View SolutionIn ΔPQR,∠PQR=90∘,
seg QS⊥ seg PR then find x,y,z.
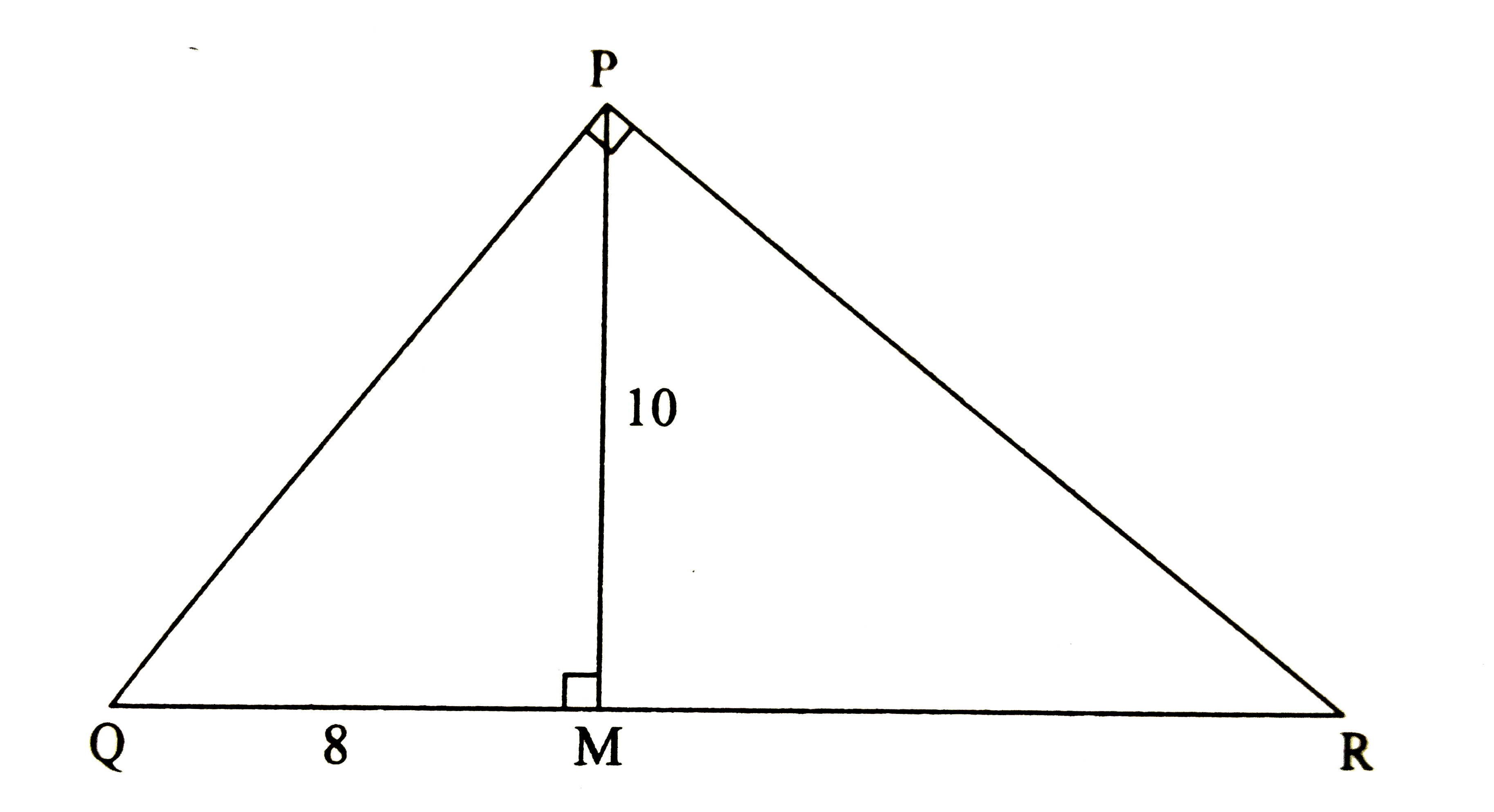
View SolutionIn the figure, ∠QPR=90∘, seg PM⊥ seg QR and Q−M−R, PM=10. QM=8, find QR.
View SolutionIn the figure , ∠PQR=32∘ seg SN ⊥ray QP and seg SM ⊥ ray QR . Find ∠ PQS . state the reason for your answer.
View SolutionIn the given figure, ∠P≅∠R , seg PQ ≅ seg RQ. Prove that ΔPQT≅ΔRQS .
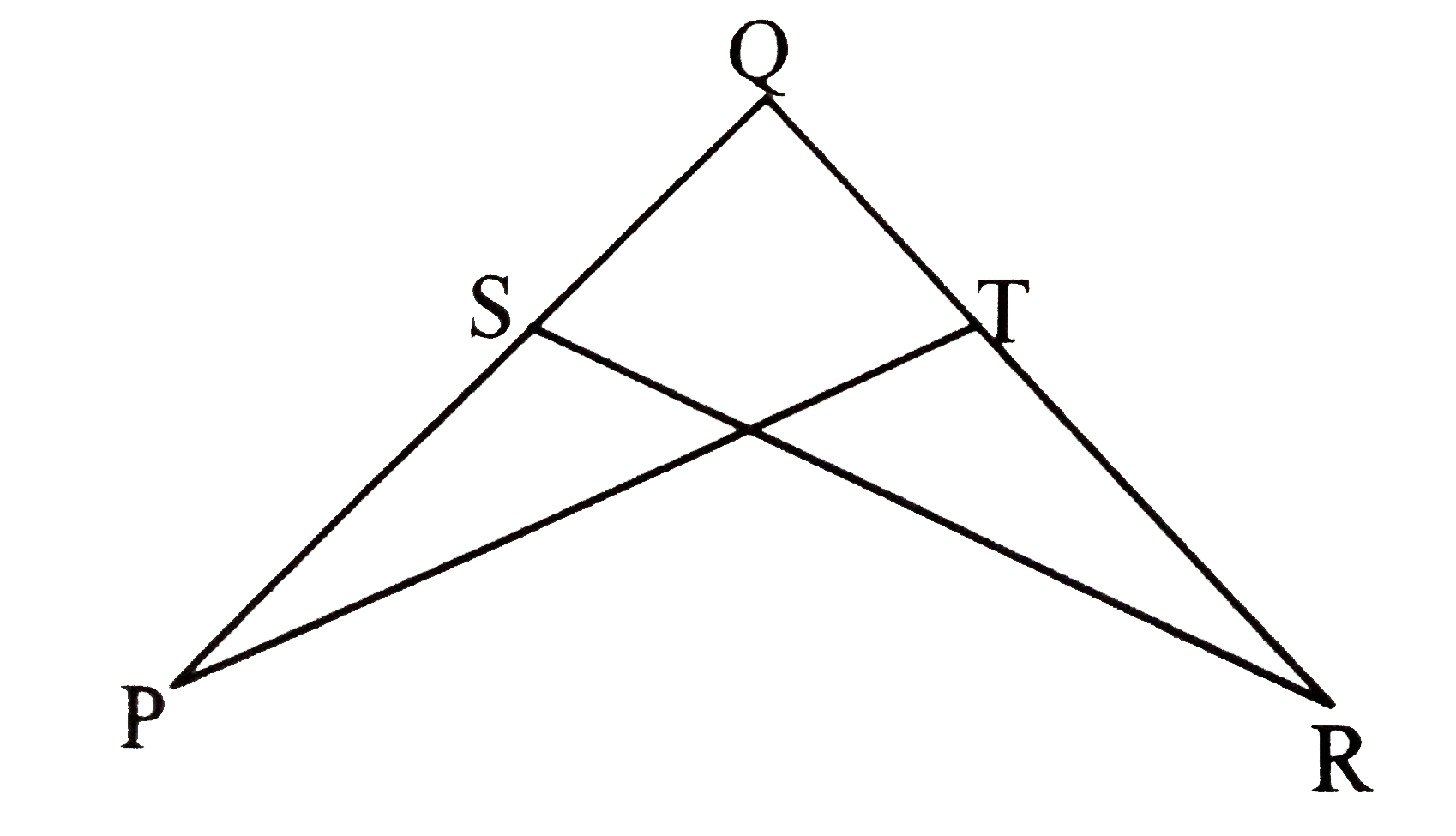
View Solution∠PQR=90∘,segQn⊥segPR,PN=9,NR=16. Find QN.
View Solution
