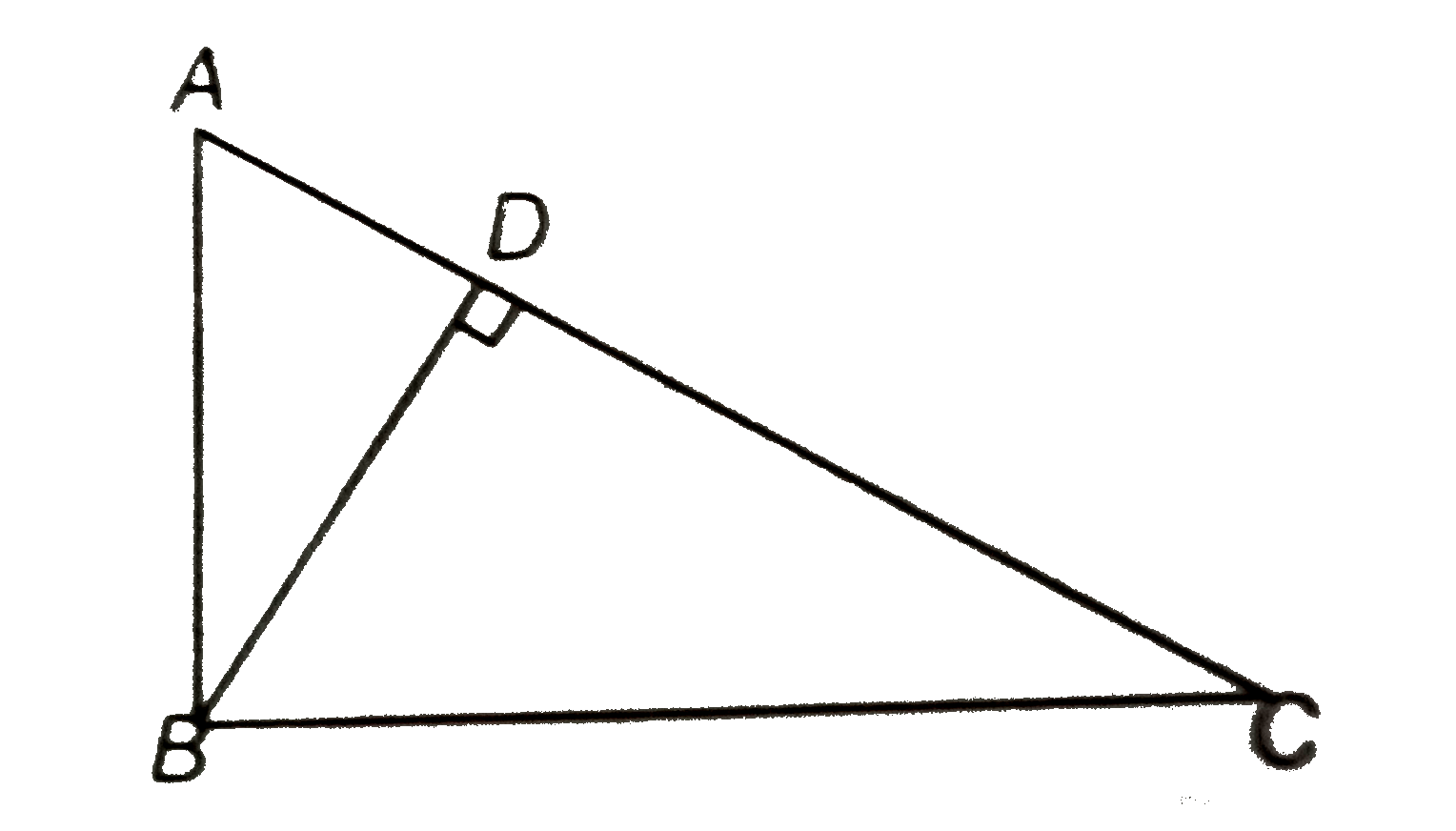
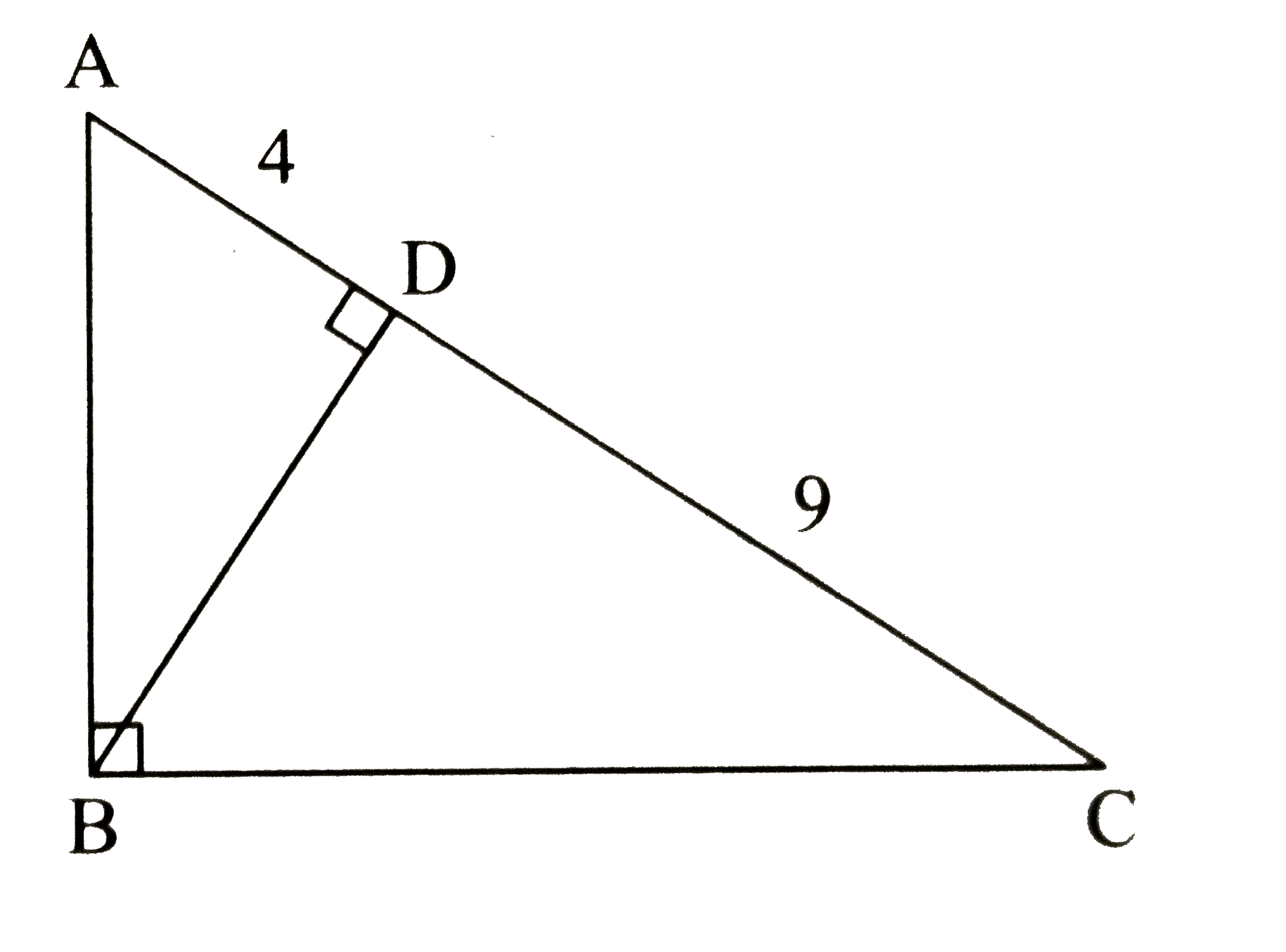
In right angled ΔABC, BD⊥AC. If AD=4, DC=9, then find BD.
Video Solution
Text Solution
The correct Answer is:BD = 6
|
Answer
Step by step video & image solution for In right angled DeltaABC, BDbotAC. If AD=4, DC=9, then find BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 3 MARK QUESTIONS )
8 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 2 MARK QUESTIONS )
2 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 1 MARK MULTIPLE CHOICE QUESTIONS )
11 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.4
12 Videos
- QUADRATIC EQUATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATION EXERCISE - CHALLENGIN QUESTIONS
2 Videos
Similar Questions
Knowledge Check
ΔABC is a right triangle , right angled at A and AD⊥BC . If AB= c and AC = b, then AD is equal to
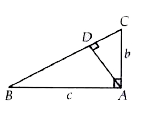 Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of these
Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of theseIn ΔABC,∠A is right angle and AD is perpendicular to BC . If AD=4cm,BC=12 cm, then value of (cotB+cotC) is
A6B3C4D32In. the figure the angles BAD and ADC are right angles and AE I I BC, if AB = BC = 5 cm and DC= 9 cm, find AD.
 A3 cmB4 cmC12 cmD6 cm
A3 cmB4 cmC12 cmD6 cm
In the given figure, ∠ABC=90∘andBD⊥AC. If BD=8cm,AD=4cm find CD.
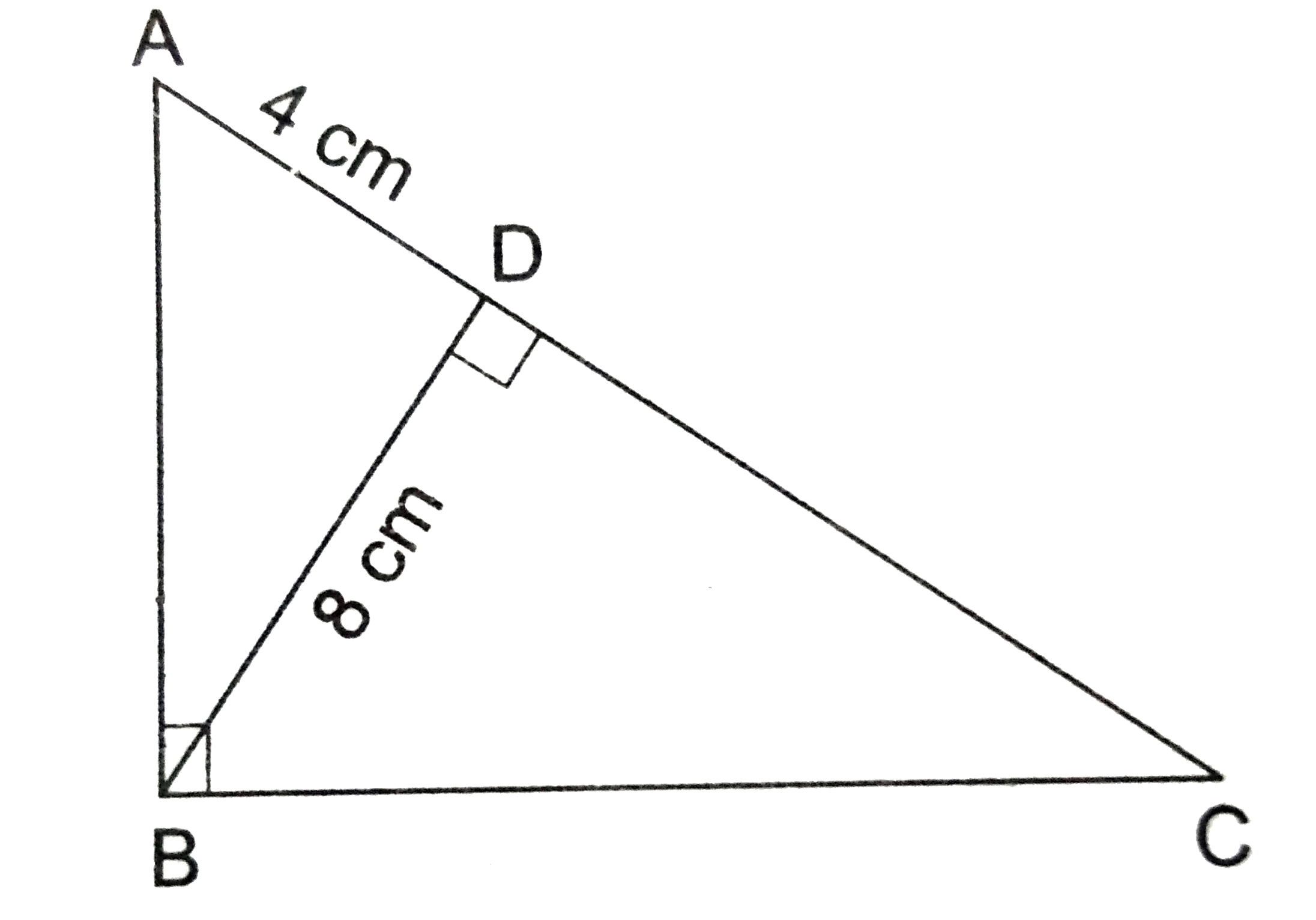
View Solution9. In Fig. 6. 18, ABC is a triangle right angled at B and BD1 AC. If AD 4 cm, and CD 5 cm, find BD and AB Fig. 6.1
View SolutionIn ΔABC, ∠A is right angle and AD is perpendicular to BC. If AD=4cm,BC=12cm, then value of (cotB+cotC)=
View SolutionIn ΔABC,∠B=90∘,BD⊥AC,A−D−C. If CD=2 cm and AD=8cm then BD is equal to
View SolutionIn ΔABC set BD bisects ∠ABC. If AB−x,BC=x+5,AD=x−2,DC=x+2, then find the value of x.

View Solution