P and Q are points on the sides CA and CB respectively of ABC , right angled at C . Prove that AQ2+BP2=AB2+PQ2 .
Step by step video & image solution for P and Q are points on the sides C A and C B respectively of A B C , right angled at C . Prove that A Q^2+B P^2=A B^2+P Q^2 . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - PROBLEM SET-2
30 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.4
12 Videos
- QUADRATIC EQUATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATION EXERCISE - CHALLENGIN QUESTIONS
2 Videos
Similar Questions
Knowledge Check
P and Q are points on the sides CA and CB respectively of ABC , right angled at C . Prove that AQ2+BP2=AB2+PQ2 .
ABC2+PQ2BAB2+PC2CAB2+PQ2DBC2+AC2
In a ABC , P and Q are point on the sides AB and AC respectively, such that PQBC . If AP=2.4cm , AQ=2cm , QC=3cm and BC=6cm , find AB and PQ .
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
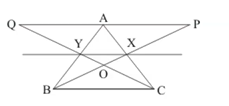
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
View SolutionIn ABC , P and Q are points on sides AB and AC respectively such that PQBC . If AP=4cm, PB=6cm and PQ=3cm , determine BC .
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn ABC , points P and Q are on CA and CB , respectively such that CA=16cm , CP=10cm , CB=30cm and CQ=25cm . Is PQ∣∣AB ?
View Solution
