In the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
seg AP || seg BQ
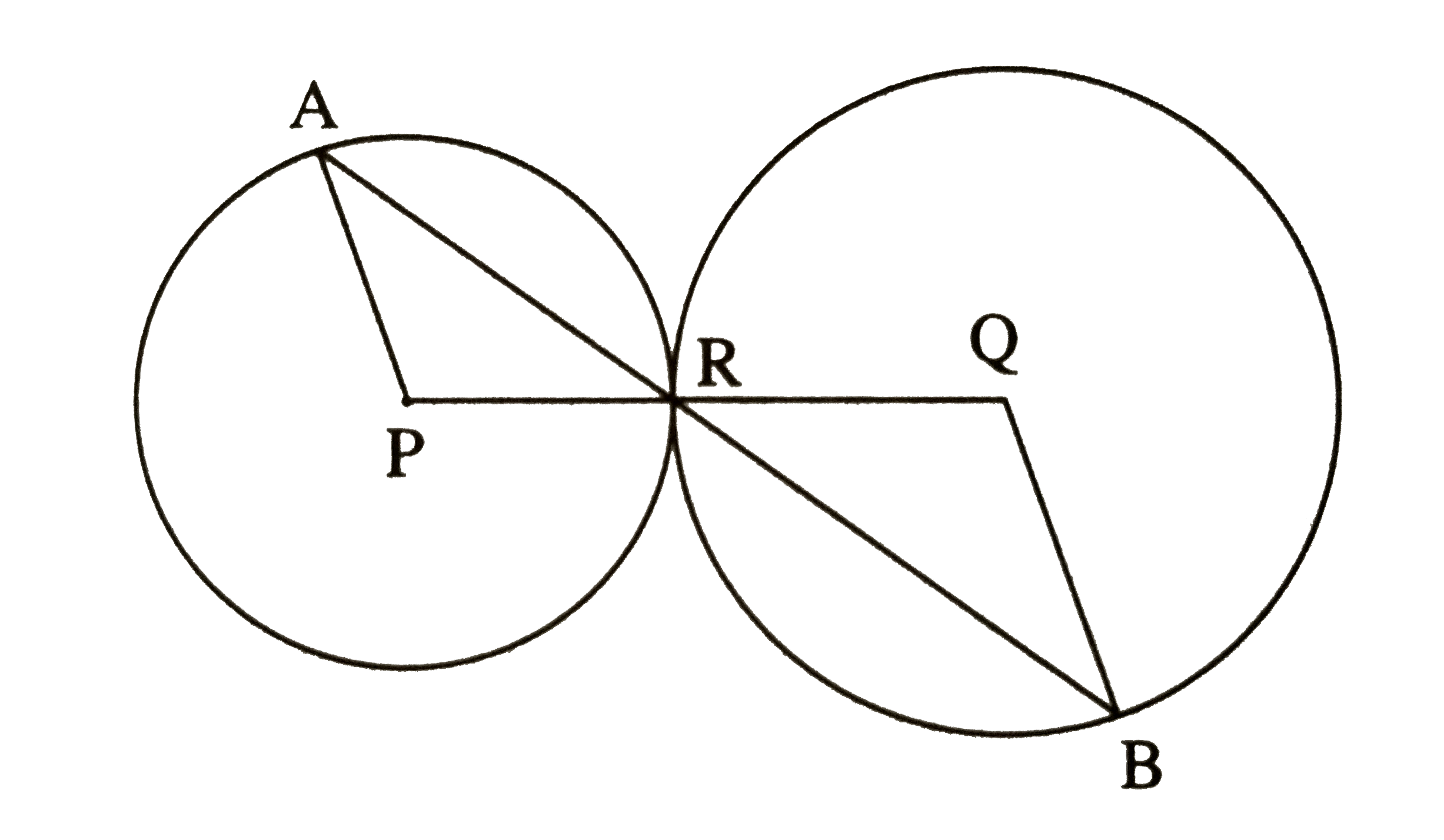
P−R−Q ……..( By theorem of touching circles )
In △PAR,
segPA≅segPR …….( Radii of the same circle )
∴∠PAR≅∠PRA …….( Isosceles triangle theorem )…….(i)
In △QRB,
segQR≅segQB …….( Radii of the same circle )
∴∠QRB≅∠QBR …….( Isosceles triangle theorem )…….(ii)
∠PRA≅∠QRB ........( Vertically opposite angles ).........(iii)
∴ From (i),(ii) and (iii), we get ,
∠PAR≅∠QBR
i.e.∠PAB≅∠QBA ...........(A−R−B)
∴segAP∣∣segBQ ......( Alternate angles test for parallel lines )
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.33videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.415videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.19videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
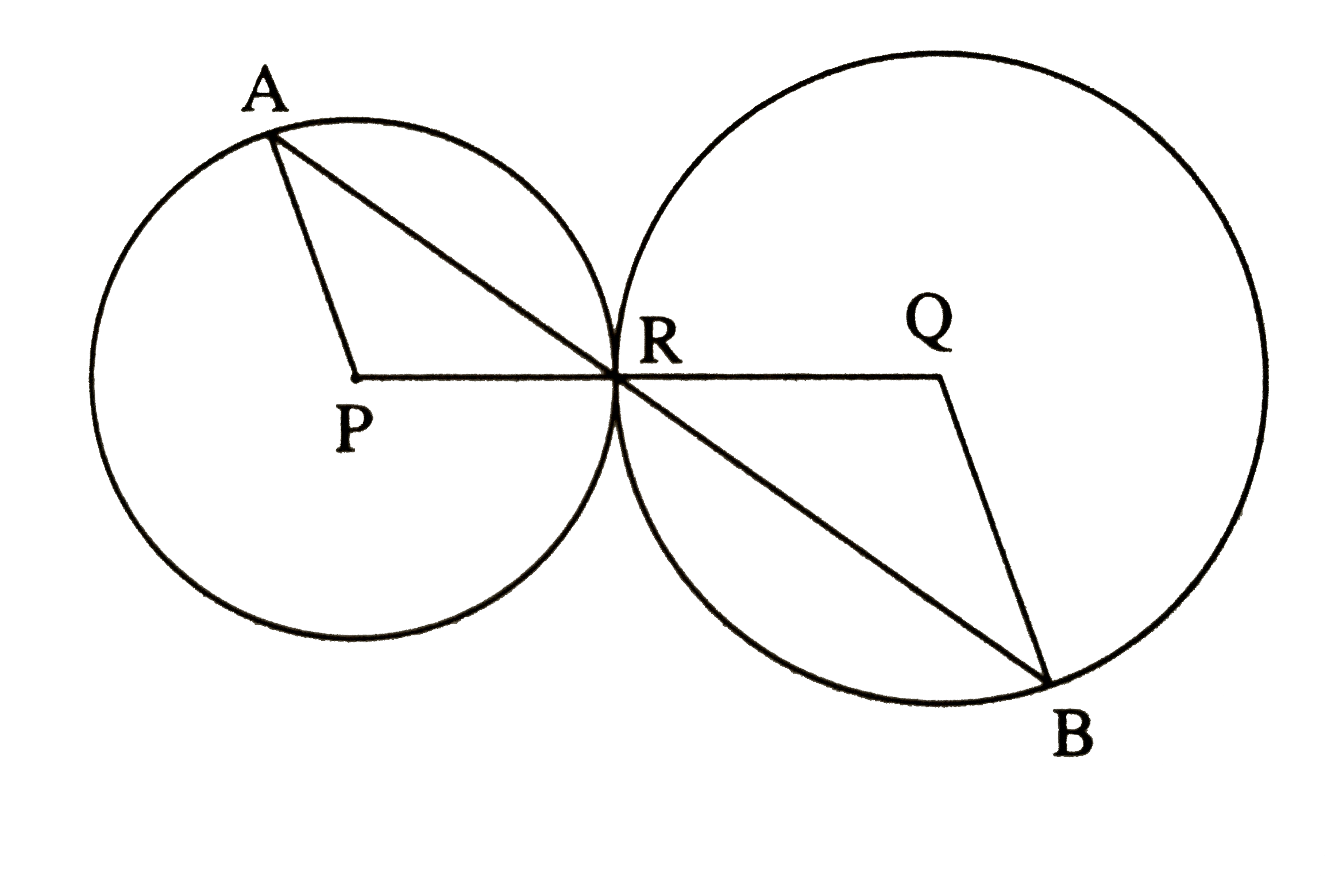
In the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
△APR~△RQB
 View Solution
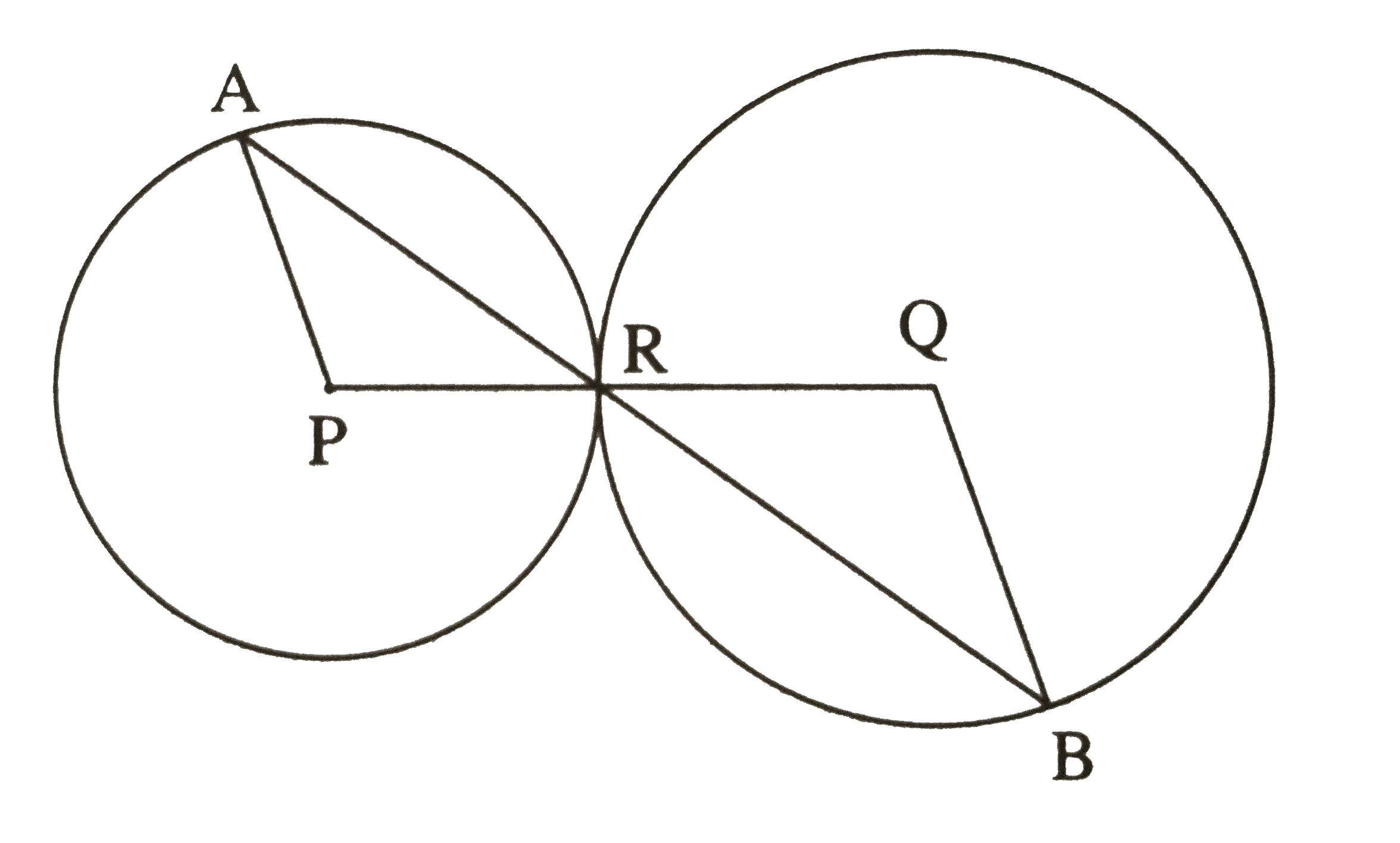
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively.
Find ∠RQB if ∠PAR=35∘
 View Solution
View SolutionIn the figure, circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, raduis XA || radius YB. Fill in the blanks and complete the proof:
 View Solution
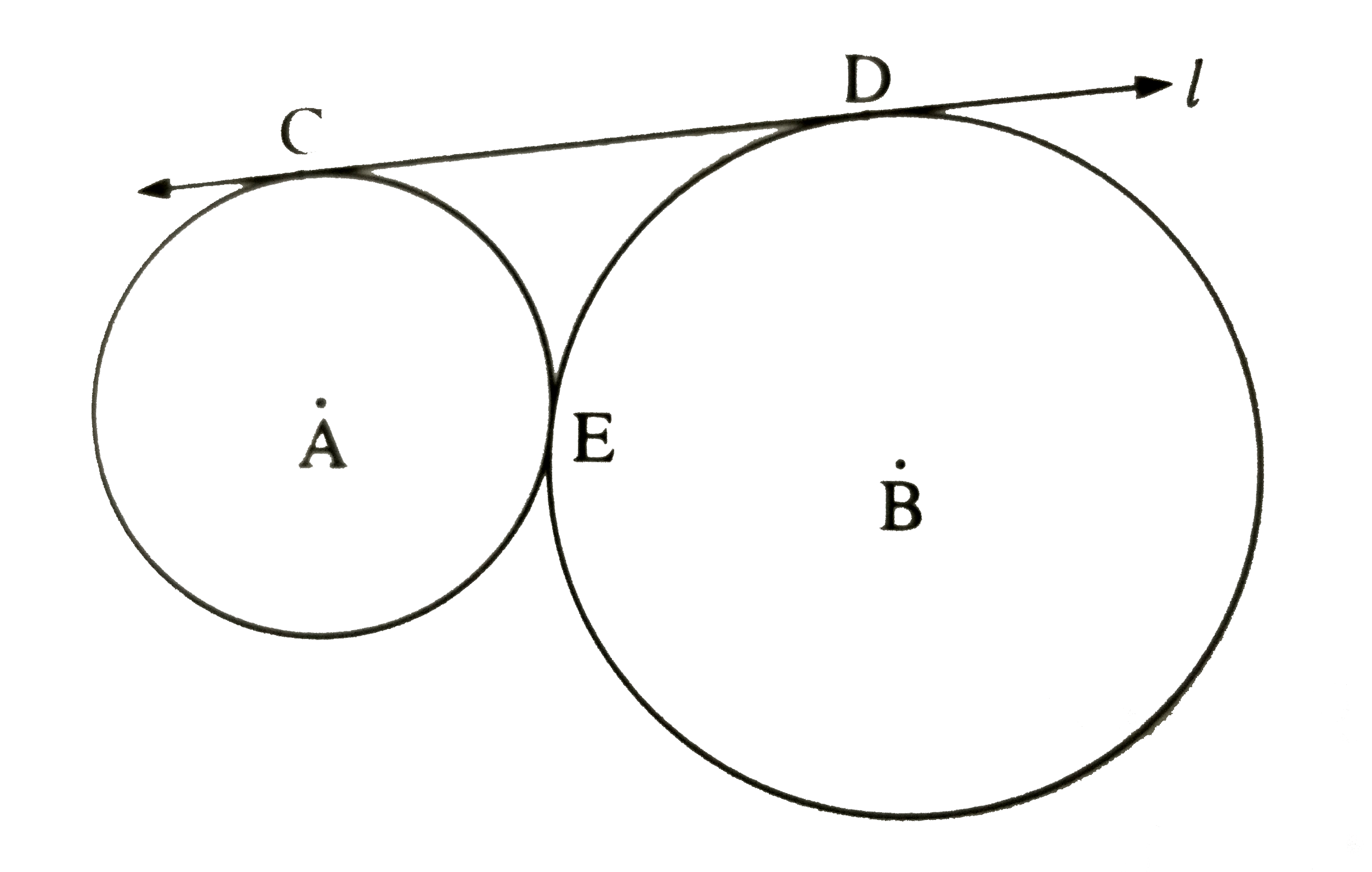
View SolutionIn the figure, the circles with centeres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD, if the radii of the circle are 4 cm, 6 cm.
 View Solution
View SolutionAs shown in the adjoining figure , two circles centred at A and B are touching at C. Line passing through C intersects the two circles at M and N respectively.
Show that seg AM ∣∣seg BN.
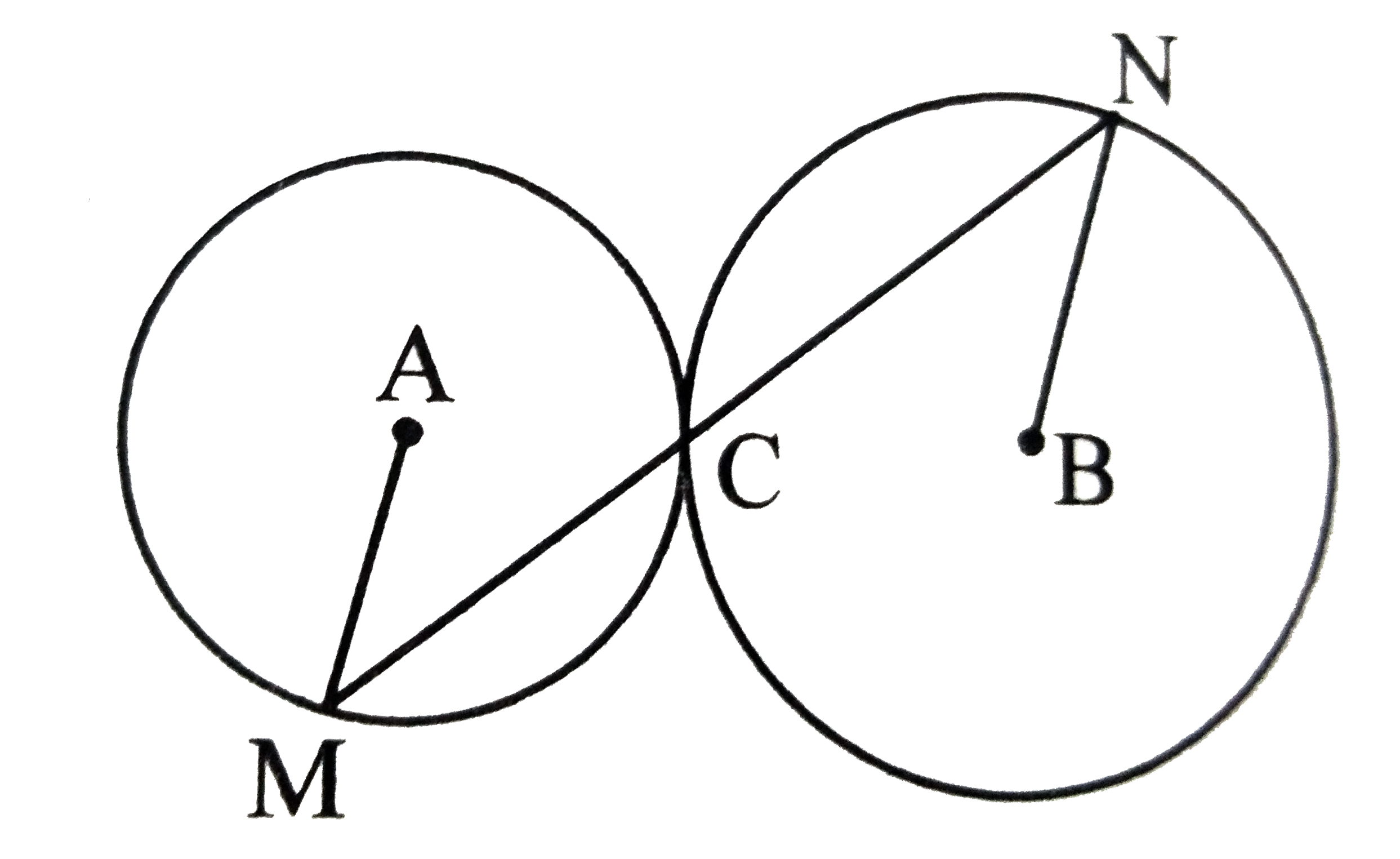 View Solution
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.
 View Solution
View SolutionIn figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ || seg RP.
 View Solution
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
 View Solution
View SolutionIn the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.
 View Solution
View Solution

