In the figure , points G,D,E,F are concyclic points of a cicle with centreC.
∠ECF=70∘
m ( arc DGF ) =200∘,
find m(arc DE) and m(arc DEF ) .

The correct Answer is:∴m(arcDE)=90∘ and m(arcDEF)=160∘
m(arcEF)=∠ECF …..( Definition of measure of minor arc )
∠ECF=70∘ …….( Given )
∴M(arcEF)=70∘
m(arcDGF)+m(arcEF)+m(arcDE)=360∘
……( Measure of a circke is 360∘)
∴200∘+70∘+m(arcDE)=360∘
∴270∘+m(arcDE)=360∘
∴m(arcDE)=360∘=270∘
∴m(arcDE)=90∘
m(arcDE)+m(arcEF)=m(arcDEF) ......( Arc addition postulate )
∴90∘+70∘=m(arcDEF)
∴m(arcDEF)=160∘
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.415videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.56videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.28videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
∠ACB is inscribed in arc ACB of a circle with centre O . If ∠ACB=65∘ , find m ( arc ACB ) .
A65∘B130∘C295∘D230∘
In the figure , if m ( arc DXE 0 =100∘ and m (arc AYC ) =40∘, find ∠DBE.
 View Solution
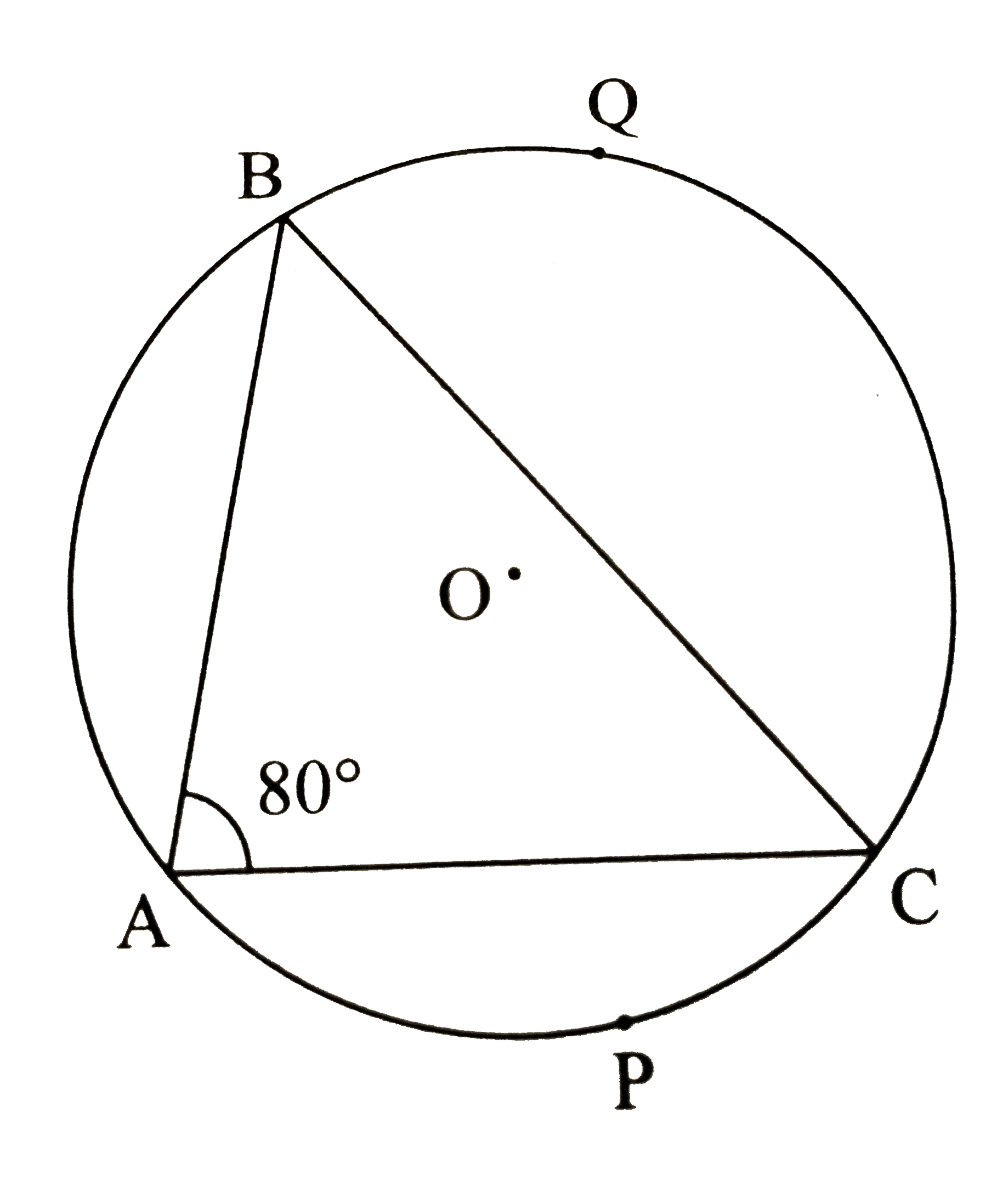
View SolutionIn the figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR=70∘ and m(arcRS)=80∘, find
(arc QS)
 View Solution
View SolutionIn the figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR=70∘ and m(arcRS)=80∘, find
(arc QSR)
 View Solution
View SolutionIn the figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR=70∘ and m(arcRS)=80∘, find
(arc PR)
 View Solution
View SolutionIn the figure , ∠QPR has its vertex outside the circle such that m ( arc QR ) = 200∘ and m ( arc ST ) =90∘, then ∠QPR= ?
 View Solution
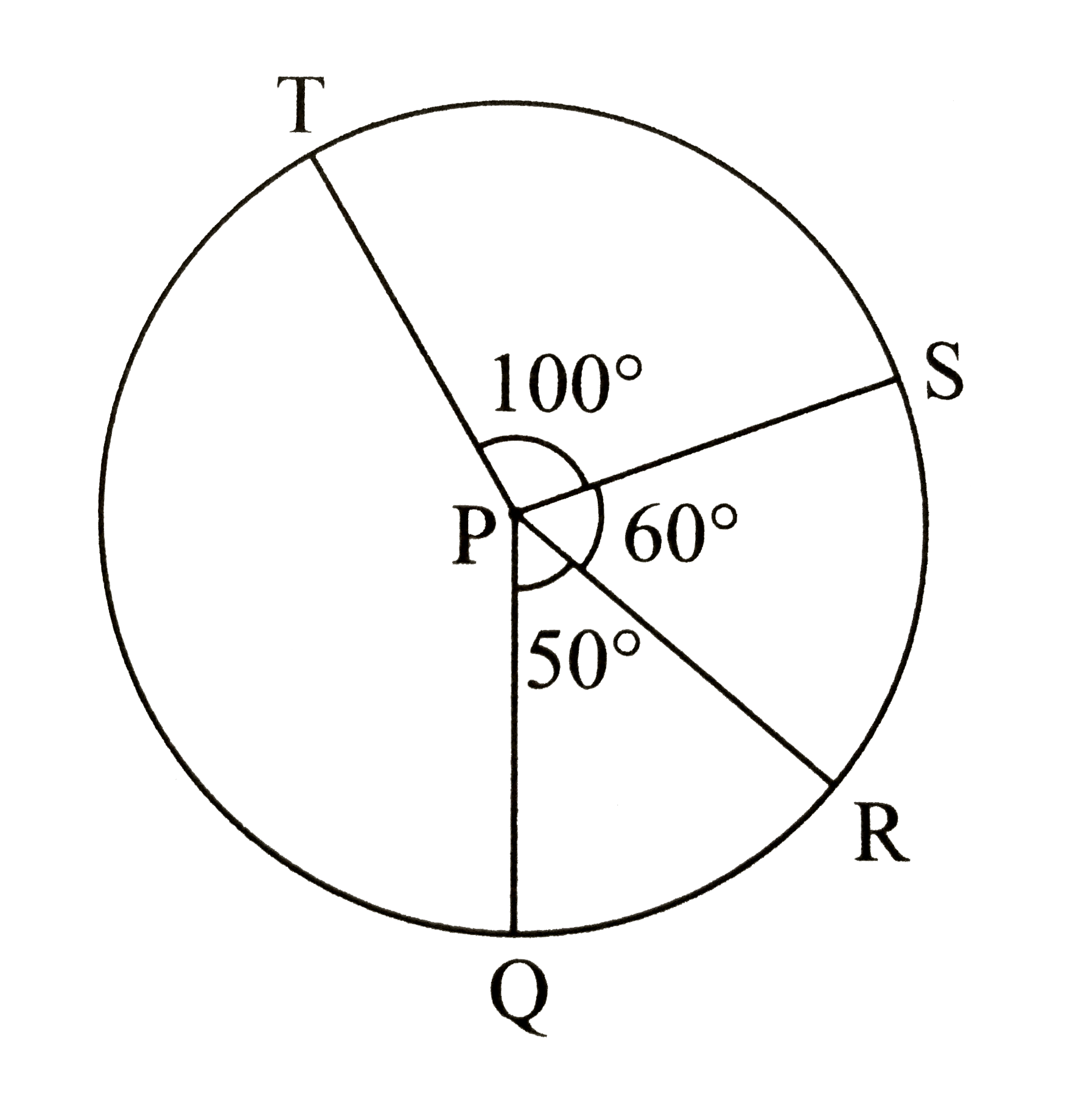
View SolutionIn the figure, P is the cnetre of the circle. If ∠QPR50∘,∠RPS=60∘,∠SPT=100∘ then find
(1) m(arc QRS) (ii) m ( arc QST ) (iii) m (arc RTS )
 View Solution
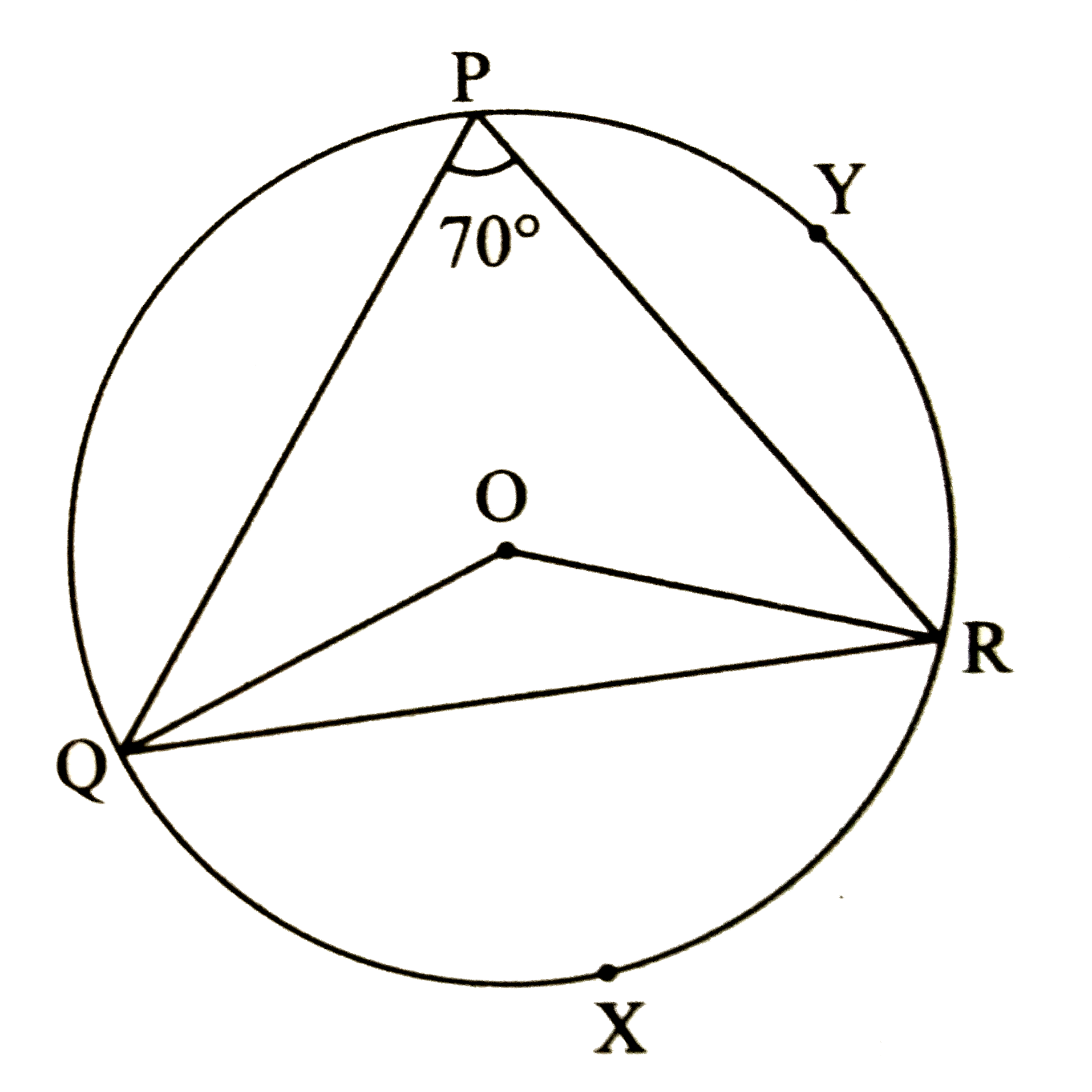
View SolutionIn the figure, O is the centre of circle ∠QPR=70∘ and m (arc PYR ) =160∘, then find the value of each of the following :
(a) m ( arc QXR )
(b) ∠QOR
(c ) ∠PQR
 View Solution
View Solution