Activity 3 :
1. Keep a glass slab on a blank paper and draw its outline PQRS.
2. Draw an inclined straight line on the side of PQ so that it intersects PQ at n. Pierce two pins vertically at two points A and B along the line.
3. Look at the pins A and B from the opposite side of the slab and pierce pins C and D vertically so that the images of A and B in line with C and D.
4. Now remove the chip and the pins and drawa straight line going through points C and D so that it intersects SR at M.
5. Join points M and N. Observe the incident rayAN and emergent ray MD.
The first refraction occurs when light ray enters the glass from air at N on the side PQ. The second refraction occurs when light enters air through the glass at point M on the side SR. For the first refraction the angle of incidence is i while for the second it is i1. The angle of refraction at N is r.
Note that i1=r. In the second refraction , the angle of refraction is e which is equal to i. On both parallel side PQ and RS of the glass slab, the change in direction of light ray is equal but in opposite directions.
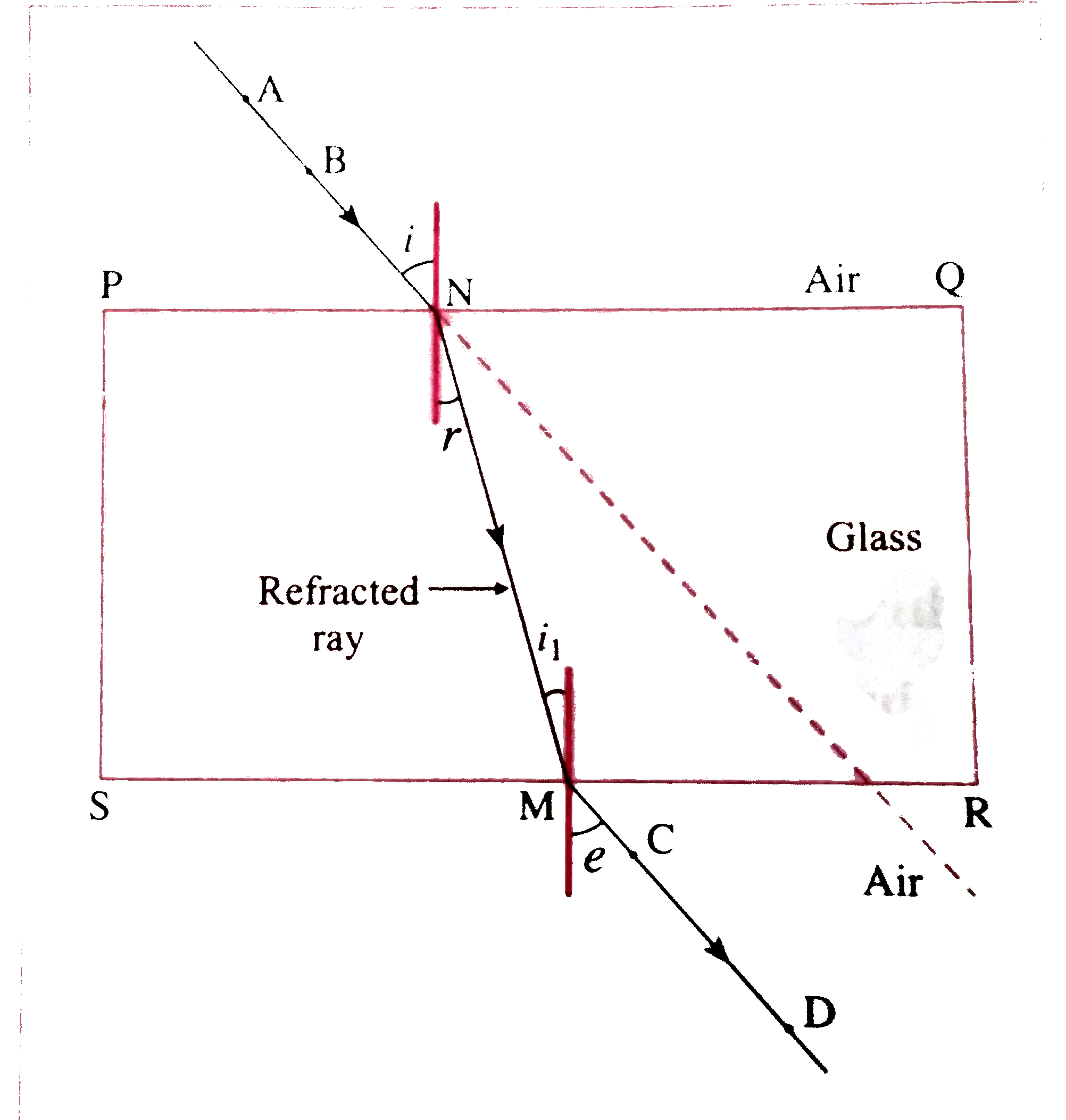
Thus, the light ray MD emerging from the glass slab is parallel to the incident ray AN on the side PQ of the slab. But the emergent ray is displaced with respect to the incident ray.
Repeat the activity "Refraction of light passing through a glass slab" by replacing the glass slab by a transparent plastic slab.
What is similarity do you observe?
Similarity : The emergent ray is parallel to the incident ray, but it is displaced sideways.
Topper's Solved these Questions
- REFRANCTION OF LIGHT BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - REFRANCTION OF LIGHT EXERCISE - TEXTBOOK 75
9 Videos
- REFRANCTION OF LIGHT BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - REFRANCTION OF LIGHT EXERCISE - Text
29 Videos
- REFRANCTION OF LIGHT BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - REFRANCTION OF LIGHT EXERCISE - ANSWER THE QUESTION
10 Videos
- QUESTIONS BASED ON THE TABLE AND FLOW CHART BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTIONS BASED ON THE TABLE AND FLOW CHART EXERCISE - Space Missions
1 Videos
- REMEDIES/MEASURES ON PROBLEMSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - REMEDIES/MEASURES ON PROBLEMSEXERCISE - CHAPTER 10 : DISASTER MANAGEMENT
1 Videos
Similar Questions
Knowledge Check
Write the following steps in sequential order to verify the laws of reflection.
(A) Draw a normal at the point where the two lines PQ and P, Q, meet. (B) Remove the pins and the mirror and join P, Q similarly join P.Q. (C) View the image of P and Q and fix two more pins P, and Q, such that the images of pins P, Q and P, Q are along the same line. (D) Draw a straight line on a white paper spread on the table and fix a plane mirror on the line. (E) Fix two pins P and Q in front of the mirror. (F) Measure the angle of incidence and angle of reflection and compare them to verify the law reflectionADABECFBACDBFECDECBAFDDBACEF
A rectangle has two opposite vertices at the points (1,2)and(5,5). If the other vertices lie on the line x=3 , find the equations of the sides of the rectangle.
View SolutionDraw lines PQ and RS intersecting at point O. Measure a pair of vertically opposite angles. Bisect them. Are the bisecting rays forming a straight line ?
View SolutionDraw a line segment PQ of length 7 cm. from a point M outside PQ, drop a perpendicular to PQ.
View SolutionConsider 2 parallel lines PQ and RS. Line PQ has two points A and B while RS has 8 points.Number of triangles that can be formed taking these 10 points as vertices of triangle is
View SolutionConstruct an angle PQR=80∘. Draw a line parallel to PQ at a distance of 3 cm from it and another line parallel to QR at a distance of 3.5 cm from it. Mark the point of intersection of these parallel lines as A.
View SolutionTwo uniform spheres A (Hollow) and B (solid) of same radius R (√125GmPr, where P is _____
View SolutionThe base PQ of two equilateral triangles PQR and PQR’ with side 2a lies along y-axis such that the mid-point of PQ is at the origin. Find the coordinates of the vertices R and R’ of the triangles.
View Solution
