Two point charges Q and −3Q are placed at some distance apart. If the electric field at the location of Q is E then at the locality of −3Q, it is
−E
E/3
−3E
−E/3
The correct Answer is:B
To solve the problem, we need to find the electric field at the location of the charge −3Q when the electric field at the location of charge Q is given as E.
1. Understanding the Setup:
We have two point charges: Q and −3Q. These charges create electric fields at each other's locations. The electric field at the location of charge Q due to charge −3Q is given as E.
2. Electric Field Due to a Point Charge:
The electric field \( E \) due to a point charge \( Q \) at a distance \( r \) is given by the formula:
\(
E = \frac{k \cdot |Q|}{r^2}
\)
where \( k \) is Coulomb's constant.
3. Electric Field at Charge Q:
The electric field \( E \) at the location of charge Q due to charge −3Q can be expressed as:
\(
E = \frac{k \cdot |-3Q|}{r^2} = \frac{3kQ}{r^2}
\)
Here, \( r \) is the distance between the charges.
4. Electric Field at Charge −3Q:
Now, we need to find the electric field \( E' \) at the location of charge −3Q due to charge Q. Using the same formula:
\(
E' = \frac{k \cdot |Q|}{r'^2}
\)
where \( r' \) is the distance from charge Q to charge −3Q. Since the distance between the two charges is the same, we can use the same \( r \) for simplicity.
5. Relating the Electric Fields:
We know from the principle of superposition that the force on charge Q due to −3Q is equal to the force on charge −3Q due to Q. Therefore, we can set up the relationship:
\(
Q \cdot E = (-3Q) \cdot E'
\)
This implies:
\(
E' = -\frac{E}{3}
\)
6. Magnitude of Electric Field:
The magnitude of the electric field at the location of charge −3Q is:
\(
|E'| = \frac{E}{3}
\)
The negative sign indicates that the direction of the electric field at −3Q is opposite to that at Q.
Final Answer:
Thus, the electric field at the locality of −3Q is:
\(
E' = -\frac{E}{3}
\)
We have two point charges: Q and −3Q. These charges create electric fields at each other's locations. The electric field at the location of charge Q due to charge −3Q is given as E.
The electric field \( E \) due to a point charge \( Q \) at a distance \( r \) is given by the formula:
\(
E = \frac{k \cdot |Q|}{r^2}
\)
where \( k \) is Coulomb's constant.
The electric field \( E \) at the location of charge Q due to charge −3Q can be expressed as:
\(
E = \frac{k \cdot |-3Q|}{r^2} = \frac{3kQ}{r^2}
\)
Here, \( r \) is the distance between the charges.
Now, we need to find the electric field \( E' \) at the location of charge −3Q due to charge Q. Using the same formula:
\(
E' = \frac{k \cdot |Q|}{r'^2}
\)
where \( r' \) is the distance from charge Q to charge −3Q. Since the distance between the two charges is the same, we can use the same \( r \) for simplicity.
We know from the principle of superposition that the force on charge Q due to −3Q is equal to the force on charge −3Q due to Q. Therefore, we can set up the relationship:
\(
Q \cdot E = (-3Q) \cdot E'
\)
This implies:
\(
E' = -\frac{E}{3}
\)
The magnitude of the electric field at the location of charge −3Q is:
\(
|E'| = \frac{E}{3}
\)
The negative sign indicates that the direction of the electric field at −3Q is opposite to that at Q.
Thus, the electric field at the locality of −3Q is:
\(
E' = -\frac{E}{3}
\)
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Motion
37 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Gauss'S Law
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Charges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View SolutionTwo point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.

View Solution
Knowledge Check
Two points charges q and -2q are placed some distance d apart. If the electric field at the location of q is E, that at the location of -2q is
A−E2B−2ECE2D−4EThe point charges Q and −2Q are placed at some distance apart. If the electirc field at the location of Q is E, the electric field at the location of −2Q will be
A−3E2B−EC−E2D−2ETwo point charges Q and −Q/4 are separated by a distance X. Then
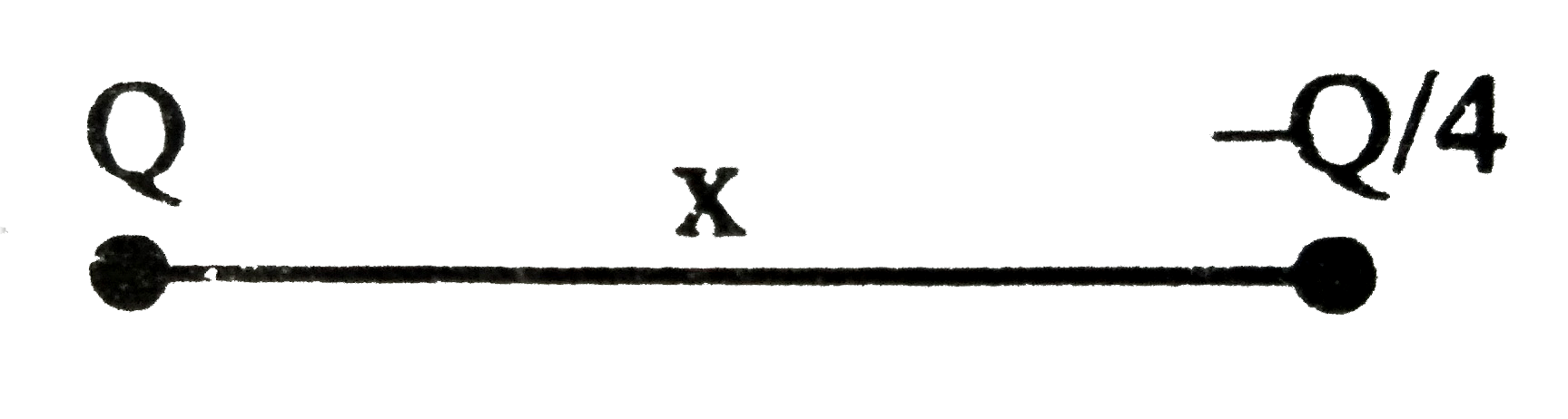 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
Two point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionTwo charges 4q and q are placed 30 cm. apart. At what point the value of electric field will be zero
View SolutionTwo charges 4q and q are placed 30 cm. apart. At what point the value of electric field will be zero
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
View Solution
