An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
Same in both cases
More in the case of electron
More in the case of proton
Independent of charge
The correct Answer is:c
To solve the problem, we need to analyze the motion of both the electron and the proton in a uniform electric field. Let's go through the steps systematically.
Step 1: Understanding the Forces
When an electron is placed in a uniform electric field E, it experiences a force given by:
F=qE
where q is the charge of the electron. The charge of the electron is −1.6×10−19C. The direction of the force on the electron is opposite to the direction of the electric field because the electron has a negative charge.
For a proton, which has a charge of +1.6×10−19C, the force will be in the same direction as the electric field.
Step 2: Calculating the Acceleration
Using Newton's second law, the acceleration a of the electron can be calculated as:
ae=Fme=qEme
where me is the mass of the electron, approximately 9.11×10−31kg.
For the proton, the acceleration ap is:
ap=Fmp=qEmp
where mp is the mass of the proton, approximately 1.67×10−27kg.
Step 3: Finding the Time of Fall
Assuming both particles start from rest and fall through a distance s, we can use the equation of motion:
s=12at2
Rearranging this gives:
t=√2sa
For the electron:
te=√2sae=√2smeqE
For the proton:
tp=√2sap=√2smpqE
Step 4: Comparing the Times
Now, we can compare te and tp:
te=√2smeqEandtp=√2smpqE
Since me (mass of the electron) is much smaller than mp (mass of the proton), it follows that:
te<tp
Conclusion
Thus, the time taken for the electron to fall through the distance s is less than the time taken for the proton to fall through the same distance in the electric field.
Final Answer
The time of fall for the electron is less than that for the proton.
---
When an electron is placed in a uniform electric field E, it experiences a force given by:
F=qE
where q is the charge of the electron. The charge of the electron is −1.6×10−19C. The direction of the force on the electron is opposite to the direction of the electric field because the electron has a negative charge.
Using Newton's second law, the acceleration a of the electron can be calculated as:
ae=Fme=qEme
where me is the mass of the electron, approximately 9.11×10−31kg.
ap=Fmp=qEmp
where mp is the mass of the proton, approximately 1.67×10−27kg.
Assuming both particles start from rest and fall through a distance s, we can use the equation of motion:
s=12at2
Rearranging this gives:
t=√2sa
te=√2sae=√2smeqE
tp=√2sap=√2smpqE
Now, we can compare te and tp:
te=√2smeqEandtp=√2smpqE
te<tp
Thus, the time taken for the electron to fall through the distance s is less than the time taken for the proton to fall through the same distance in the electric field.
The time of fall for the electron is less than that for the proton.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Gauss'S Law25videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field Due To Point Charge25videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
Similar Questions
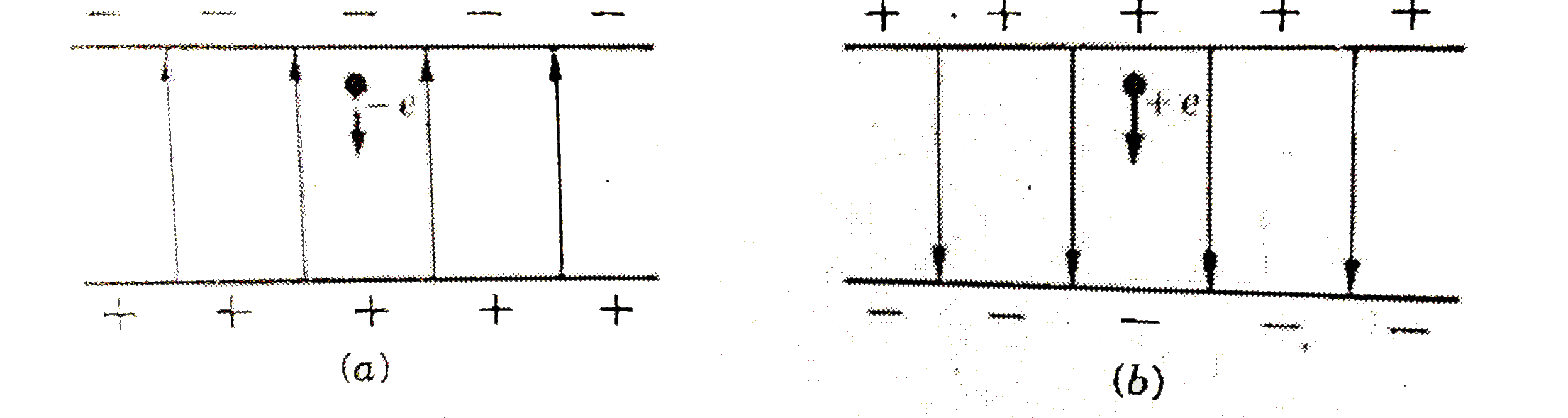
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
 View Solution
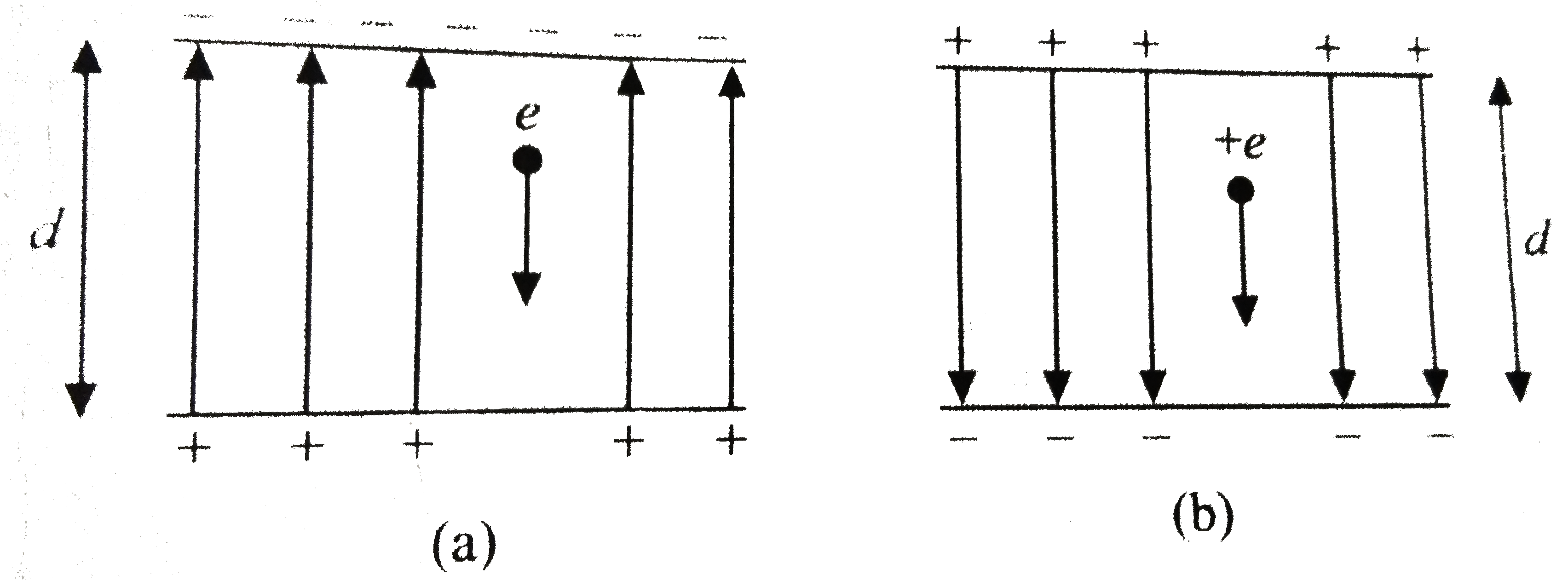
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.View Solution
Knowledge Check
- Question 1 - Select One
An electron initially at rest falls a distance of 2 cm in a uniform electric field of magnitude 3×104NC−1. The time taken by the electron to fall to this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.75×10−9s - Question 2 - Select One
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−2sC1.6×10−10sD2.9×10−9s - Question 3 - Select One
An electron falls from rest through a vertical distance h in a uniform and vertically upwards directed electric field E. The direction of electric field is now reversed , keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall proton is
A10 times greaterB5 times greaterCSmallerDEqual
An electron falls through a distance of 1.5cm in a uniform electric field of value 2×104N/C, opposite to direction of fall. Compare the time of fall with 'free fall under gravity'.
View SolutionA proton falls dwon through a distance of 2 cm in a uniform electric field of magnitude 3.34×103NC−1. Determine (i) the acceleration of the electron (ii) the time taken by the proton to fall through the distance of 2 cm, and (iii) the direction of the electric field.
View SolutionAn electron falls through a distance 1.5 cm in a uniform electric field of magnitude 2.0×104NC−1 .Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed keeping its magnitude uncharged , calculate the time taken by a proton to fall through this distance starting from rest.
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
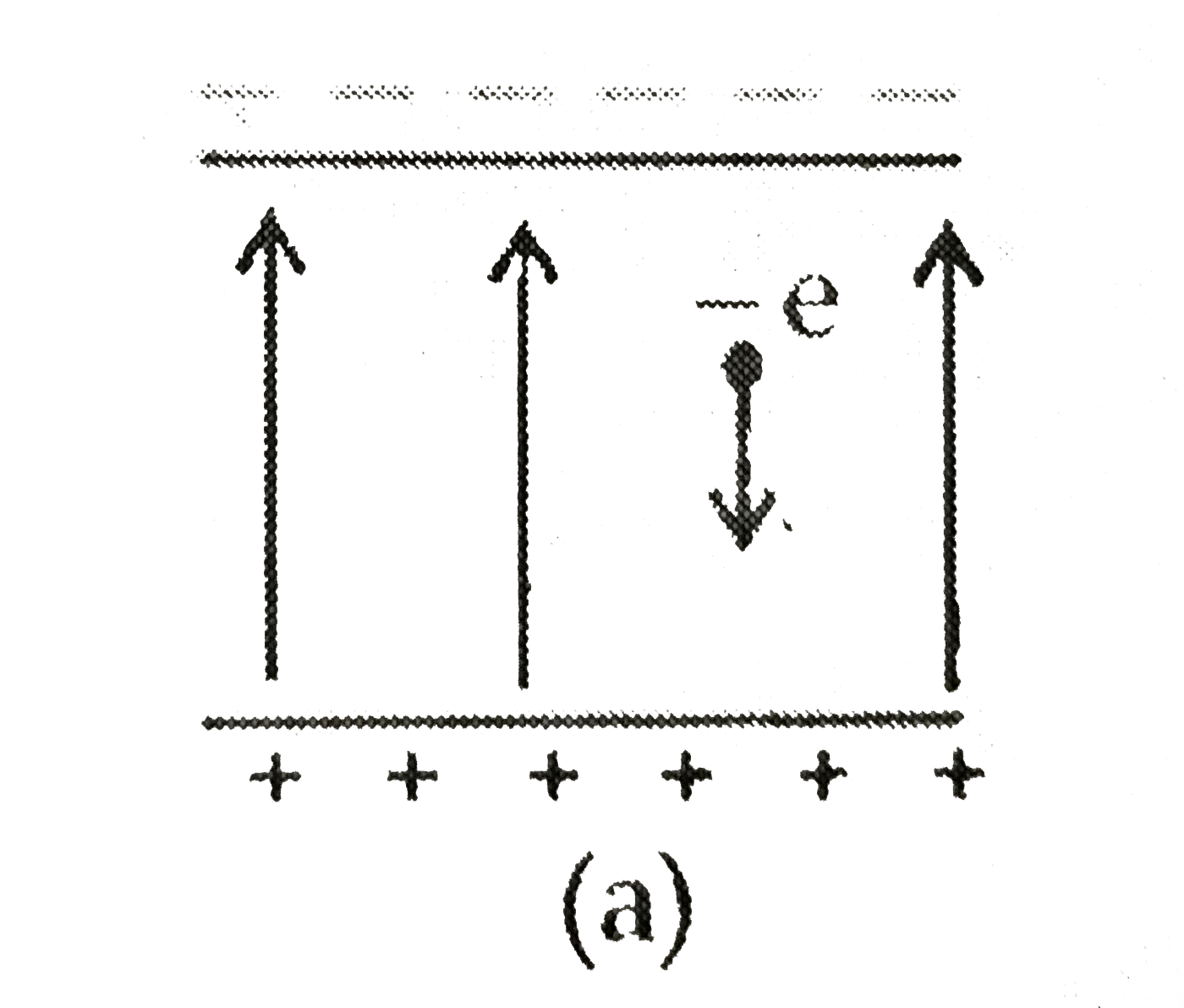
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest.
 View Solution
View SolutionAn electron falls from rest through a vertical distance h in a uniform and vertically upwards directed electric field E. The direction of electric field is now reversed , keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall proton is
View Solution

