If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
A
(ϕ1+ϕ2)ε0
B
(ϕ2−ϕ1)ε0
C
(ϕ1+ϕ2)/ε0
D
(ϕ2−ϕ1)/ε0
Video Solution
Text Solution
The correct Answer is:B
φnet=1ε0×Qenc⇒Qenc=(φ2−φ1)ε0
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Problems Based On Mixed Concepts40videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Motion37videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
Similar Questions
Knowledge Check
- Question 1 - Select One
If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2 then the electric charge inside the surface will he
A(ϕ+ϕ2)ε0B(ϕ2−ϕ1)ε0C(ϕ1−ϕ2)ε0D(−ϕ1−ϕ2)ε0 - Question 2 - Select One
If the electric flux entering and leaving an enclosed surface respectively is ϕ1 and ϕ2, the electric charge inside the surface will be
Aϕ3−ϕ1εnBϕ2+ϕ1εnC(ϕ1−ϕ3)εnDεn(ϕ2−ϕ1) - Question 3 - Select One
If the electric flux entering and leaving an enclosed surface are ϕ1andϕ2 respectively, then the electric charge present within the surface is
A1∈0(ϕ1+ϕ2)B1∈0(ϕ2−ϕ1)C∈0(ϕ1+ϕ2)D∈0(ϕ2−ϕ1)
Electric flux through a closed surface in free space enclosing a charge q is
View SolutionThe electric flux through the surface
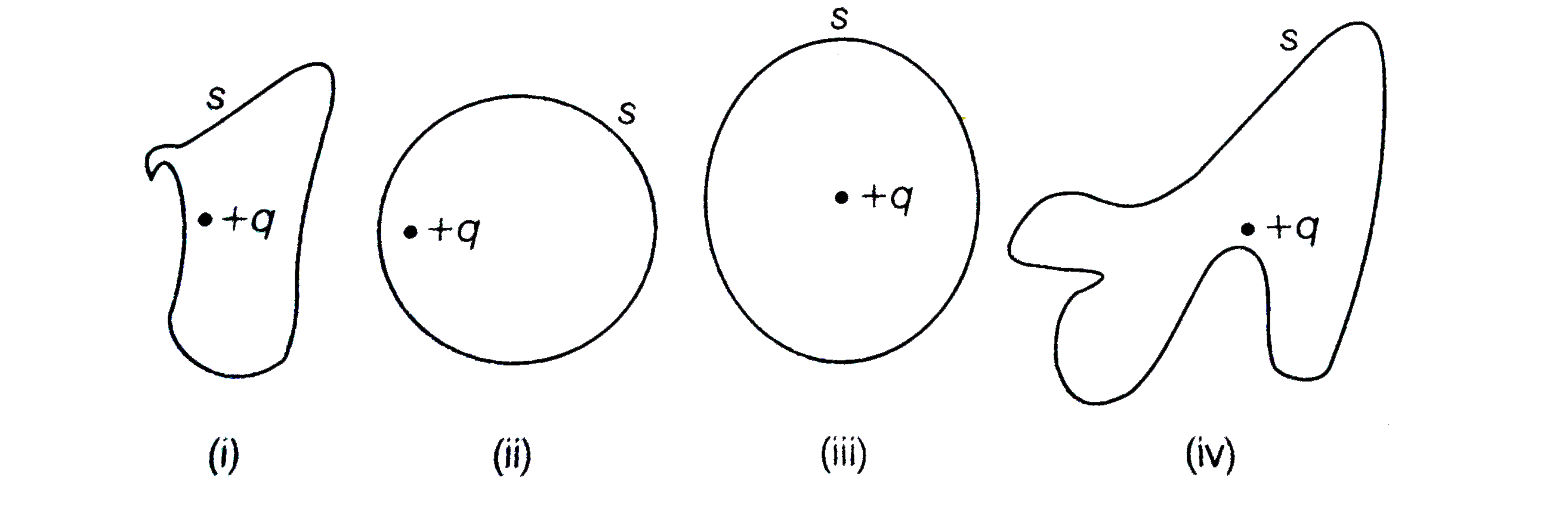 View Solution
View SolutionThe electric flux through the surface
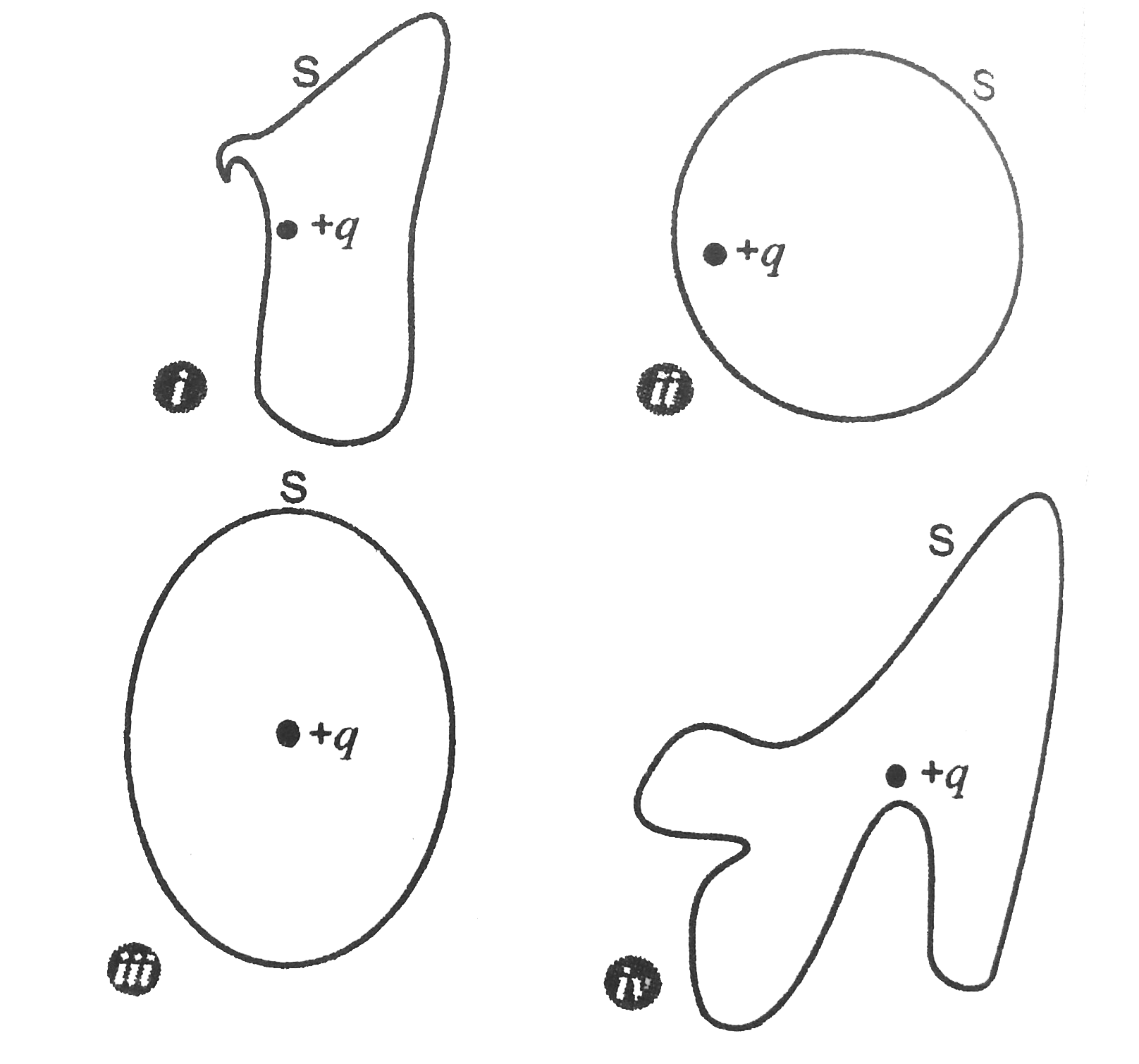 View Solution
View SolutionIf the electric flux entering and leaving a closed surface are 6×106 and 9×106 SI units respectively, then the net charge inside the surface of permittivity of free space ε0 is
View SolutionIf ϕ1andϕ2 are normal of flux entering and leaving an enclosed surface. Electric flux inside the surface will be
View Solution