In a region of space the electric field in the x-direction and proportional to xi.e., →E=E0xˆi. Consider an imaginary cubical volume of edge a with its sides parallel to the axes of coordinates. The charge inside this volume will be
zero
ε0E0a3
1ε0E0a3
16ε0E0a3
The correct Answer is:b
Field at face ABCD=−E0x0ˆi
Flux over the face ABCD=−E0x0a2
The negative sign arises as the field is directed into the cube.
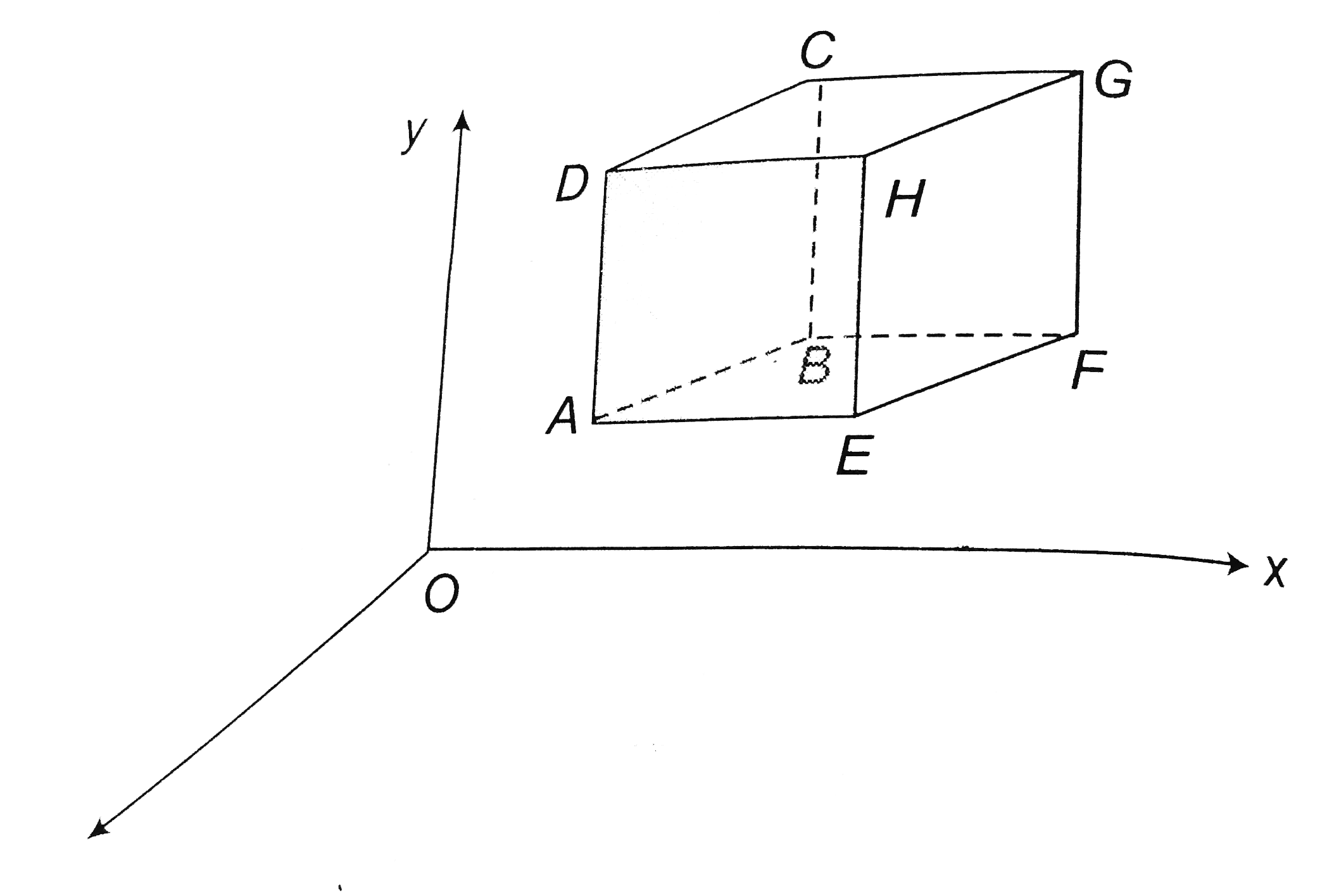
Field at face EFGH=E0(x0+a)ˆi
Flux over the face EFGH=E0(x0+a)a2
Flux over the other four faces is zero as the field is parallel to the surfaces.
Total flux over the cube =E0a3=1ε0q.
Where q si the total charge under the cube
∴q=ε0E0a3.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Problems Based On Mixed Concepts40videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Field And Motion37videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
Similar Questions
The electric fields in a region is given by →E=E0xLˆi ,Find the charge contained inside a cubical volume bounded by the surface x=0,x=L,y=0,y=L,z=0,z=L.
View SolutionIn a uniform electric field E if we consider an imaginary cubical closed surface of side a, then find the net flux through the cube ?
View Solution
Knowledge Check
- Question 1 - Select One
The electric field in a certain region is given by →E=(Kx3)→i. The dimensions of K are -
AMLT−3A−1BML−2T−3A−1CML4T−3A−1Ddimensionless
In a certain region of space the electric field increases radially as →E=90r(−ˆr) .The electric charge contained within a sphere of radius 2m centred at the origin is:
View SolutionThe electric field in a region is given by →E=E0xˆi. The charge contained inside a cubical volume bounded by the surface x=0, x=2m, y=0, y=2m, z=0 and z=2m is nε0E0. Find the va,ue of n.
View SolutionIn a certain region of space, the electric field always pointing in x - direction but its magnitude decreases from E=560N/Cat x=0 to E=410N/C at x=25m if a cubical box of side length I = 25 m is oriented, such that its four sides are parallel to the field lines, then charge enclosed by the box is......
View SolutionThe electric field in a cubical volume is
→E=E0(1+za)ˆi+E0(za)ˆj
Each edge of the cube measures d, and one of the corners lies at the origin of the coordinates. Determine the net charge within the cube.View SolutionThe electric field in a region is given by →E=E0axˆi. Find the electric flux passing through a cubical volume bounded by the surfaces x=0,x=a,y=0,y=a,z=0 and z=a.
View SolutionThe electric field in a region of space is given ¯¯¯E=E0ˆi+2E0ˆj where E0=100NC .The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly:
View SolutionThe magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View Solution

