In the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight

2√2mvε0σq
√2mvε05σq
mvε0√2σq
mvε02√2σq
The correct Answer is:a
For maximum distance angle of projection should be 45∘
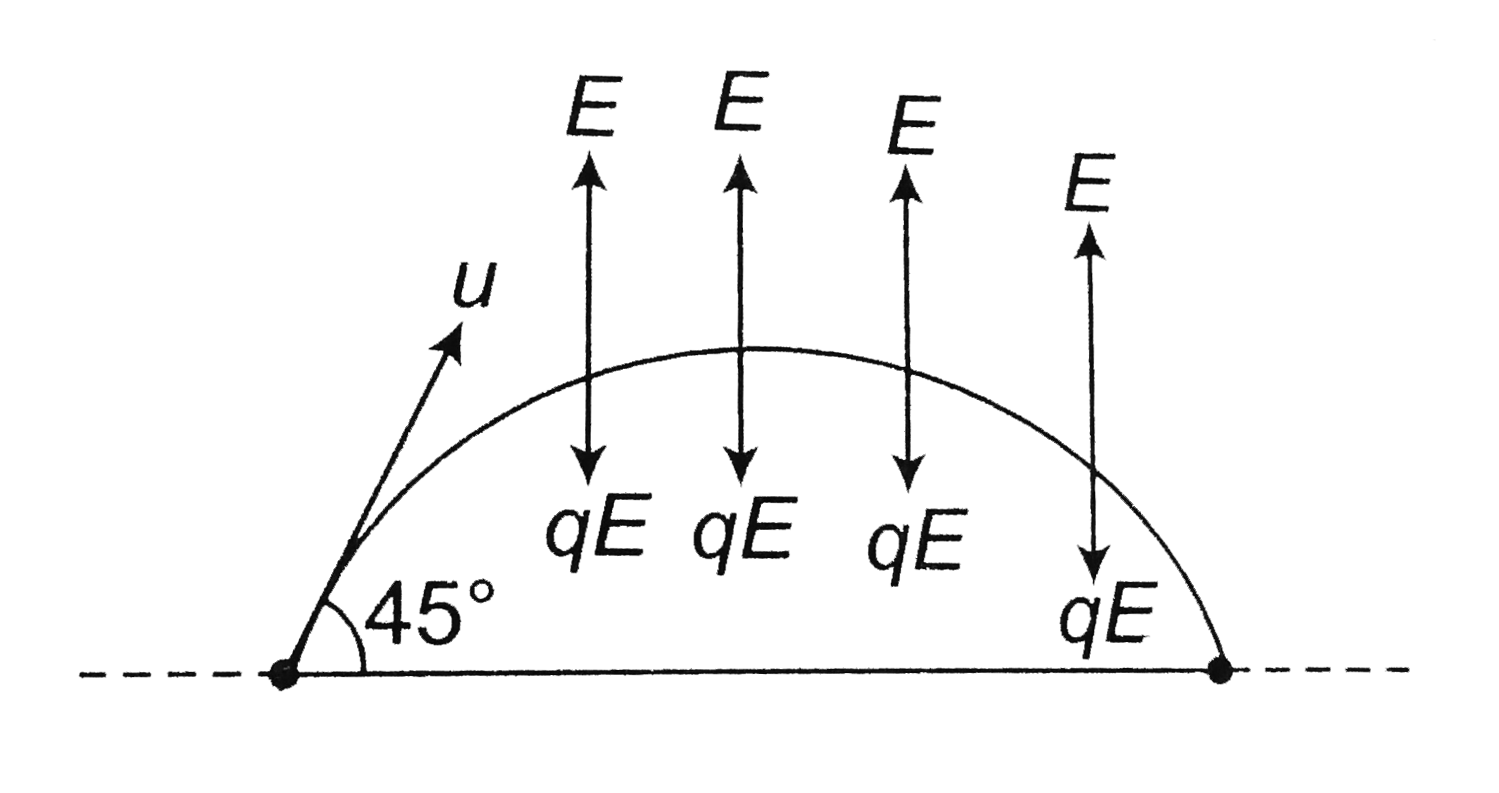
For vertical displacement, →S=→ut+12→at2
0=usin45∘t+12.q.σ2ε0mt2
t=0 or t=2√2mvε0σq
So time of flight =2√2mvε0σq
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning25videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions24videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
Similar Questions
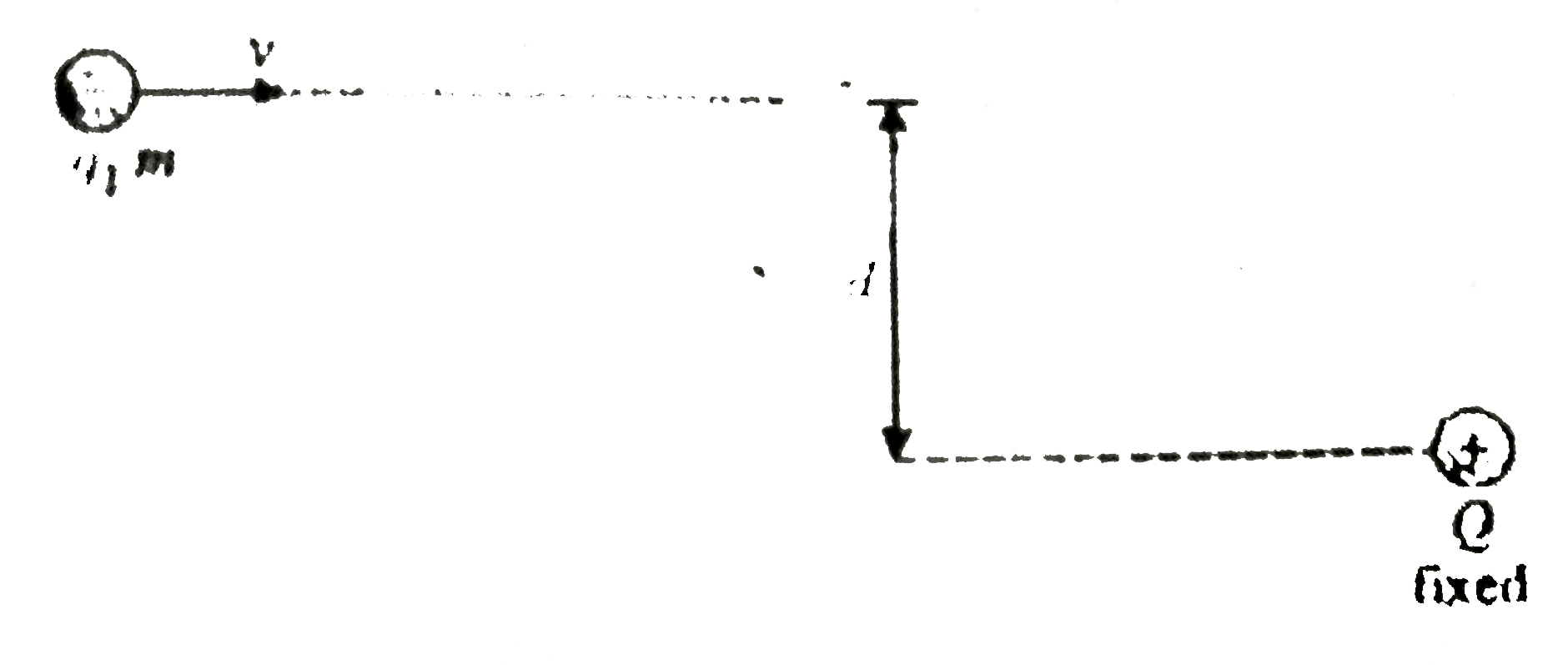
Figure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
 View Solution
View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
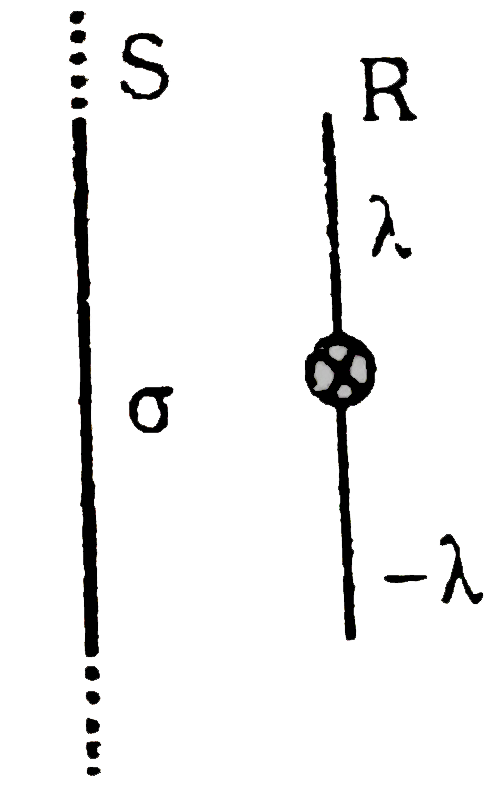 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.
 AMagnetic field at P is μ0i4πr[2+√2]⊙BThe magnetic field at P is μ0i/2πr.CThe particle initially accelerated towards wire A.DThe particle initially accelerated towards wire B.
AMagnetic field at P is μ0i4πr[2+√2]⊙BThe magnetic field at P is μ0i/2πr.CThe particle initially accelerated towards wire A.DThe particle initially accelerated towards wire B. - Question 2 - Select One
An infinite plane sheet of positive charge has surface charge density σ. A metallic ball of mass m and charge +Q is attached to a thred and is tied to a point A on the sheet PQ. The angle θ made by the string with plane sheet is in equilibrium is
AzeroBtan−1(Qσ4ε0mg)Ctan−1(Qσ2ε0mg)Dtan−1(Qσε0mg) - Question 3 - Select One
A charged particle of charge q and mass m enters a magnetic field as shown. Find radius of the circular path and the time spent inside the field. Neglect gravity.
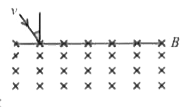 ARπθvBR(π−2θ)vCR(π+2θv)D2Rθv
ARπθvBR(π−2θ)vCR(π+2θv)D2Rθv
An infinitely large plate of surface charge density +σ lying in horizontal xy plane. A particle having charge −q0 and mass m is projected from the plate with velocity u making an angle θ with sheet. Find :
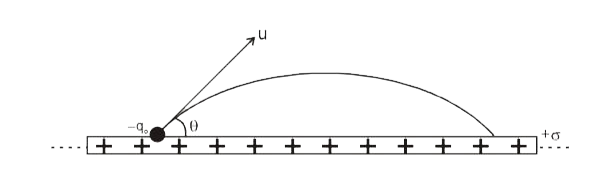
(i) the time taken by the particle to return on the plate.
(ii) maximum height achieved by the particle.
(iii) At what distance will it strike the plate (Neglect gravitational force on the particle)View SolutionIn the figure shown, S is a large non-conducting sheet of uniform charge density σ. A rod R of length I and mass m is parallel to the sheet and hinged at its midpoint. The linear charge densities on the upper and lower half of the rod are shown in the figure. The angular acceleration of the rod just after it is released is pσλqmɛo. Find pq.
'(##CEN_KSR_PHY_JEE_C18_E01_031_Q16##)'View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released
[3σλ2m∈0]
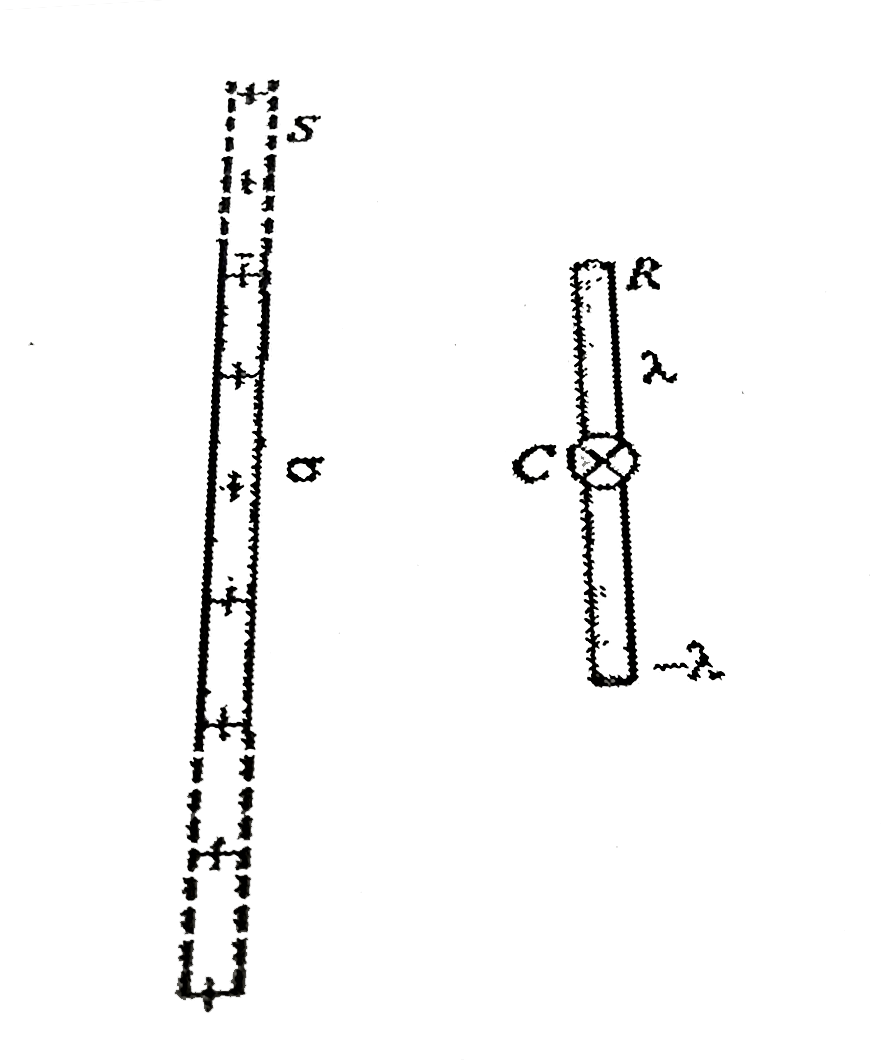 View Solution
View SolutionAn infinitely large plate of surface charge density +σ is lying in horizontal xy-plane. A particle having charge −q0 and mass m is projected from the plate with velocity u making an angle θ with sheet. Find :

(i) The time taken by the particle to return on the plate.
(ii) Maximum height achieved by the particle.
(iii) At what distance will it strike the plate (Neglect gravitational force on the particle)View SolutionAn infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
View Solution

