A conic surface is placed in a uniform electric field E as shown in figure. Such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is θ.

Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux (θ<45∘).
A
ER[hcosθ+π(R/2)sinθ]
B
ER[hsinθ+π(R/2)cosθ]
C
ER[hcosθ+πRsinθ]
D
none of these
Video Solution
Text Solution
The correct Answer is:A
Flux entering the cone from side AB will ultimately also pass through area A1 and A2
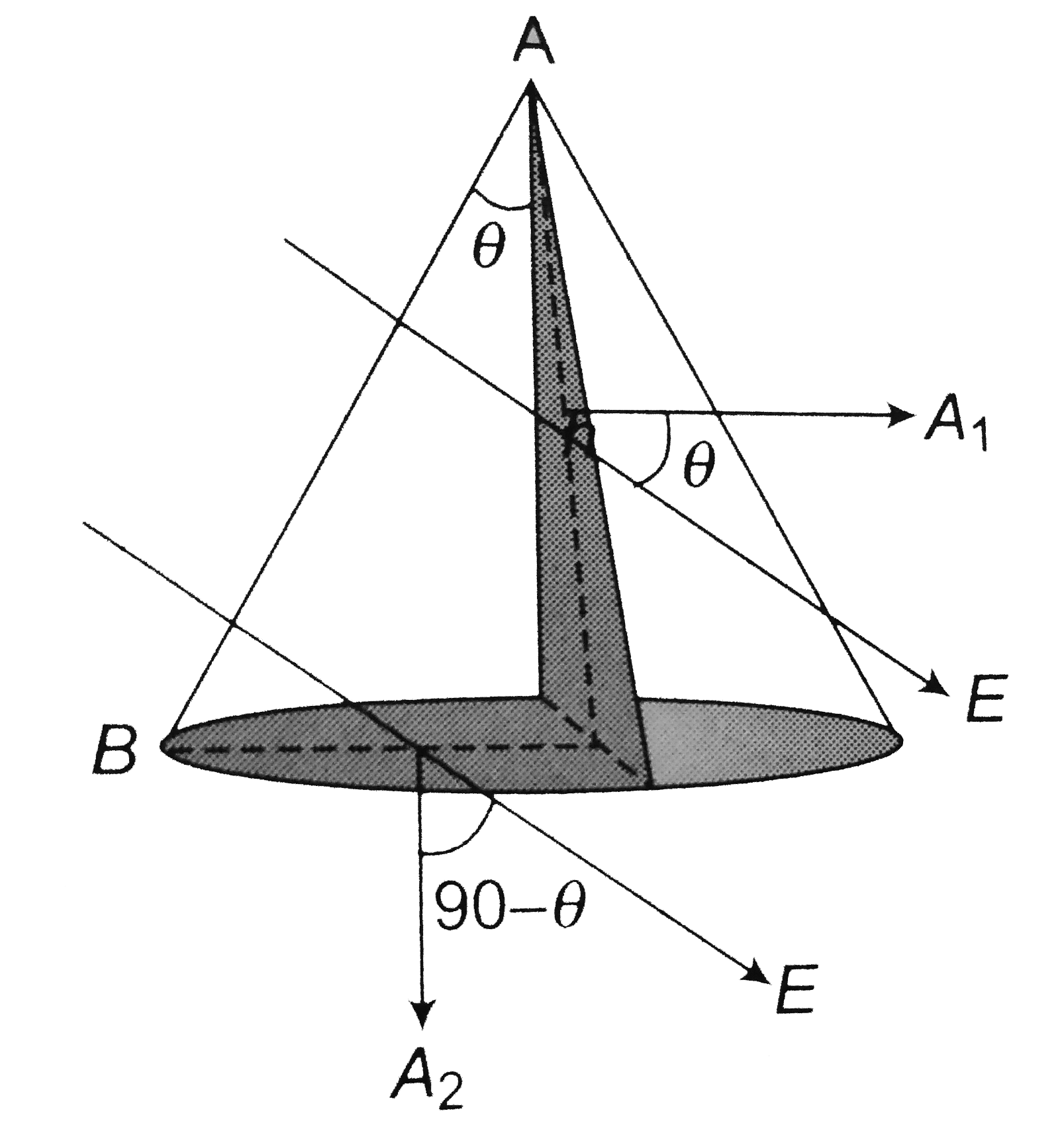
So, ϕ=EA1cosθ+EA2cos(90−θ)
E(122Rhcosθ+π2R2sinθ)
=ER(hcosθ+π(R/2)sinθ)
|
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions
24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
A cone lies in a uniform electric field E as shown in figure. The electric flux entering the cone is
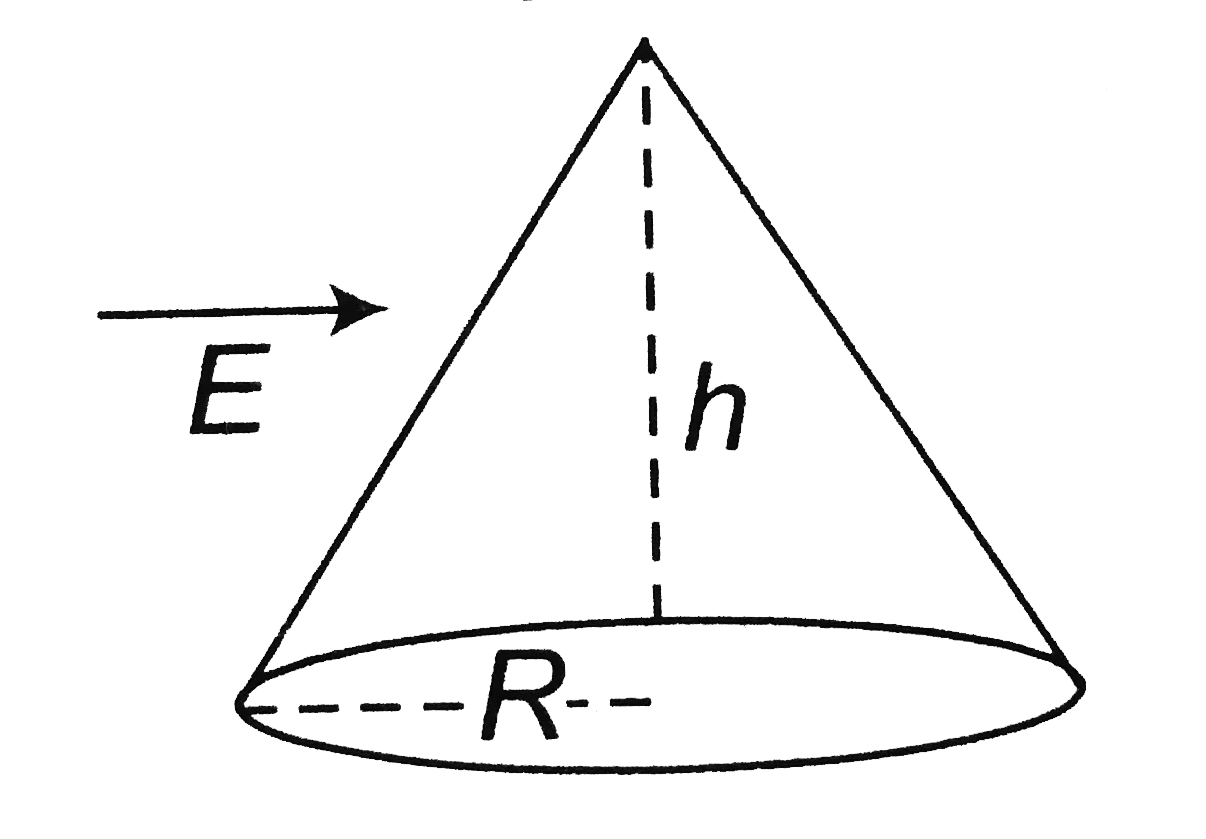 AEπR2BERhCEhR2DEh2
AEπR2BERhCEhR2DEh2The curved surface area of the cone of radius 5 cm and height 12 cm is
A60πcm2B65πcm2C300πcm2D325πcm2If the curved surface area of a cone is thrice that of another cone and slant height of the second cone is thrice that of the first, find the ratio of the area of their base.
A81:1B9:1C3:1D27:1
The height of a cone is 24 cm and the diameter of its base is 14 cm. Find the slant height, volume, area of curved surface and the cone
View SolutionThe curved surface area of a cone of base radius r and height h is_______.
View SolutionThe height of a cone is 24 cm and the diameter of its base is 14 cm. The curved surface area of the cone is
View SolutionThe area of the base of a right circular cone is 154 cm2 and its height is 14cm . Its curved surface area is
View SolutionA radius of the base of a right circular cone is 6 cm and its slant height is 28 cm. The curved surface area of the cone is----
View Solution
