A charge q is located at the centre of a cube. The electric flux through any face is
4πq6(4πε0)
πq6(4πε0)
q6(4πε0)
2πq6(4πε0)
The correct Answer is:a
To find the electric flux through any face of a cube when a charge q is located at the center, we can follow these steps:
Step 1: Understand Gauss's Law
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
Φ=Qϵ0
Step 2: Identify the Charge and the Surface
In this case, we have a charge q located at the center of a cube. The cube is a closed surface surrounding the charge.
Step 3: Calculate the Total Electric Flux
Using Gauss's Law, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
Step 4: Determine the Flux Through One Face of the Cube
Since the cube has 6 faces and the charge is symmetrically located at the center, the electric flux is uniformly distributed across all faces. Therefore, the electric flux through one face Φface can be calculated by dividing the total flux by the number of faces:
Φface=Φtotal6=q6ϵ0
Conclusion
The electric flux through any face of the cube is:
Φface=q6ϵ0
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
Φ=Qϵ0
In this case, we have a charge q located at the center of a cube. The cube is a closed surface surrounding the charge.
Using Gauss's Law, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
Since the cube has 6 faces and the charge is symmetrically located at the center, the electric flux is uniformly distributed across all faces. Therefore, the electric flux through one face Φface can be calculated by dividing the total flux by the number of faces:
Φface=Φtotal6=q6ϵ0
The electric flux through any face of the cube is:
Φface=q6ϵ0
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIIMS Questions
26 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Assertion Reason
7 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
An electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
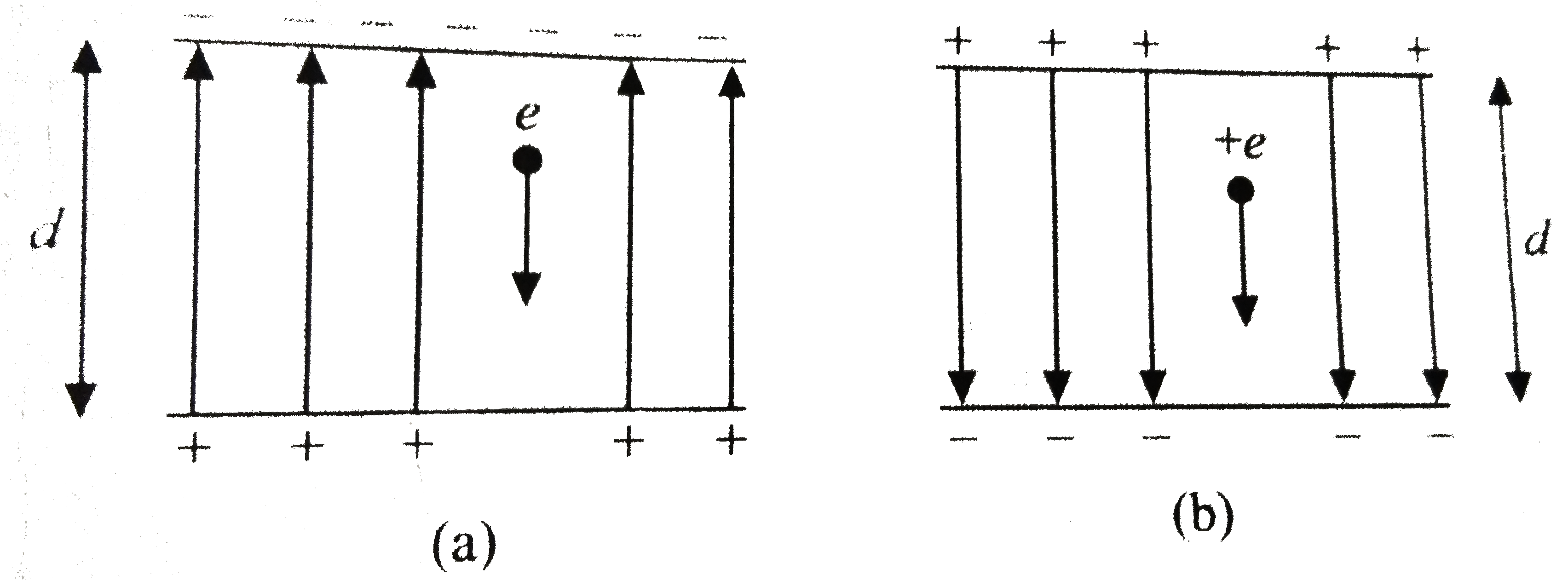 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionAssertion. A metallic shield in the form of a hollow shell, can be built to block an electric field.
Reason. In a hollow spherical shell, the electric field inside is not zero at every point.
View SolutionAssertion: Electric lines of force cross each other
Reason: Electric field at a point superimpose to give one resulant electric field
View SolutionIf a photon has velocity c and frequency n , then which of following represents its wavelength ?
View SolutionGiven: electric potential, ϕ=x2+y2+z2. The modulus of electric field at (x,y,z) is
View SolutionA charge q is placed at the centre of a cube of side l what is the electric flux passing through two opposite faces of the cube ?
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA positive charge Q is situated at the centre of cube. The electric flux through any face of the cube is (in SI units)
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View Solutionघन के एक कोने पर q आवेश रखा गया है आवेश के निकट स्थित तीन फलकों में से किसी एक से होकर गुजरने वाला विद्युत फ्लक्स O होता है | अन्य तीन फलको में से किसी एक से होकर जाने वाले फ्लक्स होगा
View SolutionA charge q is located at centre of a cube of edge length 'a' The electric flux through any force
View SolutionA charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is
View SolutionWhat will be the flux passing through the faces of a cube of length a if charge q is located
View SolutionIf a charge q is located at a centre of the hypothetical cube, the electric flux through its any face is :
View Solution
