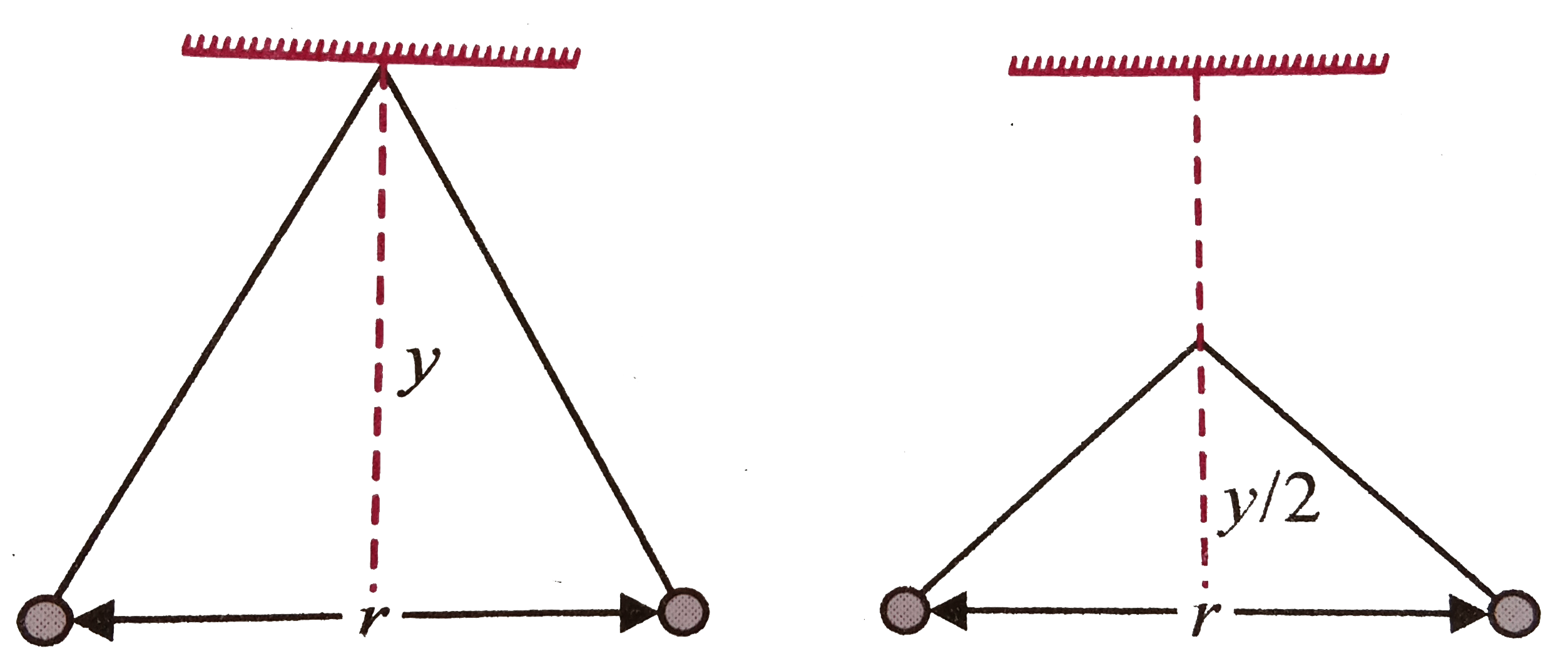
Two path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :

A

${(\frac{1}{\sqrt{2}})}^{2}$

B

$(\frac{r}{.^{3} \sqrt{2}})$

C

$(\frac{2 r}{\sqrt{3}})$

D

$(\frac{2 r}{3})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b

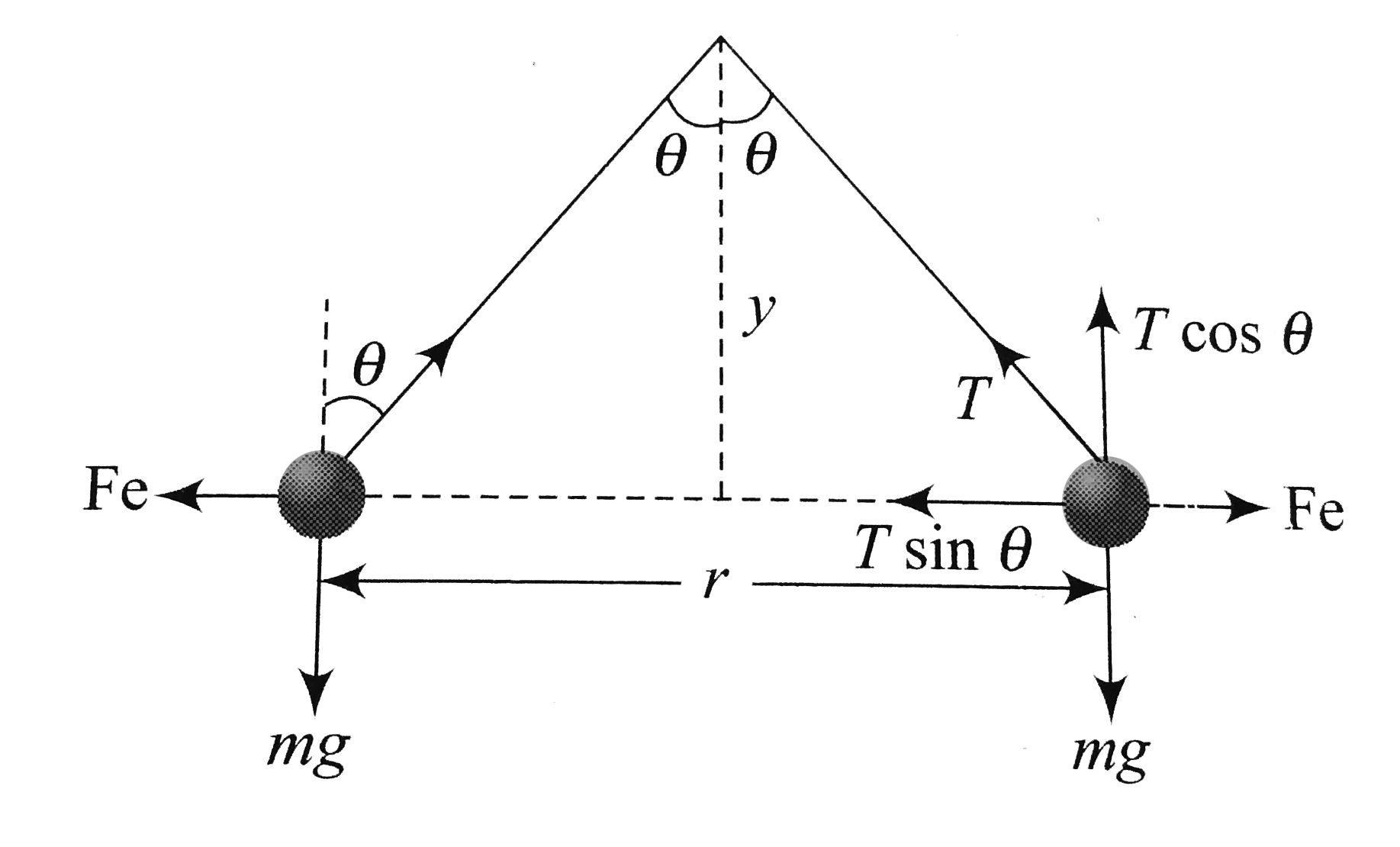
Case-1:
$T sin θ = F_{e}$ (i)

$T sin θ = F_{e}$ (i)
$T cos θ = m g$ (ii)
$tan θ = \frac{F_{e}}{m g} \Rightarrow F_{e} = m g tan θ$
Here, $F_{e} = k \frac{q^{2}}{r^{2}} = m g . \frac{r / 2}{y}$ (iii)

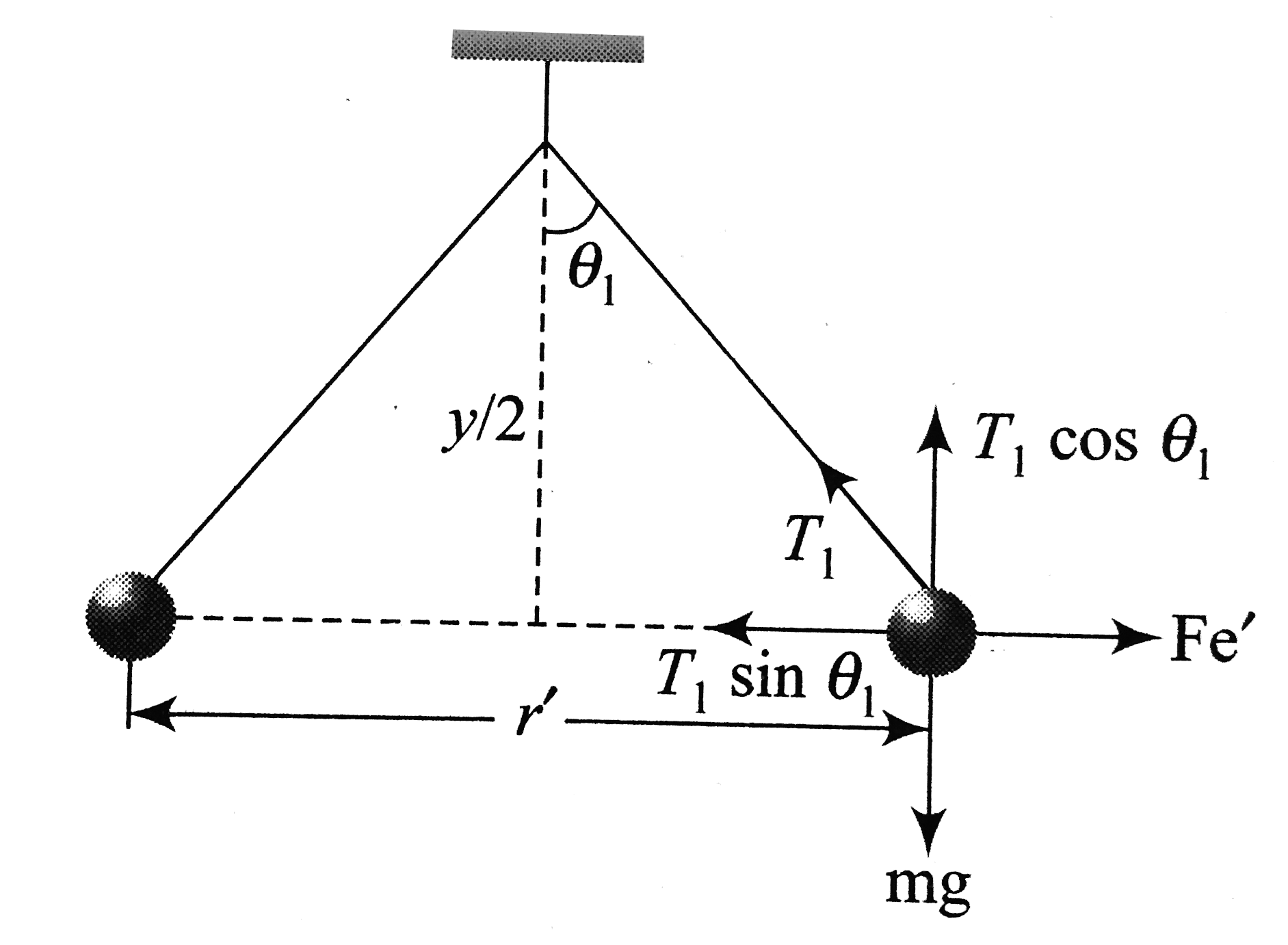
$T_{1} {sin θ}_{1} = F_{e}$ (iv)
$T_{1} {cos θ}_{1} = m g$ (v)
${tan θ}_{1} = \frac{F'_{e}}{m g} \Rightarrow F'_{e} = m g {tan θ}_{1}$ (v)
Here $F'_{e} = k \frac{q^{2}}{r^{2}} = m g . \frac{r' / 2}{y / 2}$ (vi)
From (iii) &(vi)
$\frac{k q^{2} / r^{2}}{k q^{2} / r'^{2}} = \frac{r}{2 r'}$
$\Rightarrow (\frac{r'^{2}}{r}) = \frac{1}{2}$ or $r' = \frac{r}{2^{1 / 3}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two path balls carrying eqaul chareges are suspended froom a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :

A $(\frac{2 r}{3})$
B ${(\frac{1}{\sqrt{2}})}^{2}$
C $(\frac{r}{\sqrt[3]{2}})$
D $(\frac{2 r}{\sqrt{3}})$

A2Z-ELECTRIC CHARGE, FIELD & FLUX-AIPMTNEET Questions

Home
Ask Doubt
Profile