Three capacitors of capacitance 1μF,2μF and 3μF are connected in series and a potential difference of 11V is applied across the combination. Then, the potential difference across the plates of 1μF capacitor is
2V
4V
1V
6V
The correct Answer is:D
To solve the problem of finding the potential difference across the 1 μF capacitor in a series circuit of three capacitors (1 μF, 2 μF, and 3 μF) connected across a total potential difference of 11 V, we can follow these steps:
1. Understand the Series Connection:
- In a series connection of capacitors, the total voltage across the combination is equal to the sum of the voltages across each capacitor.
- Mathematically, this can be expressed as:
Vtotal=V1+V2+V3
where V1, V2, and V3 are the voltages across the 1 μF, 2 μF, and 3 μF capacitors respectively.
2. Use the Relationship of Charge:
- In a series circuit, the charge (Q) on each capacitor is the same. The relationship between charge, capacitance, and voltage is given by:
Q=C⋅V
Therefore, we can write:
Q=C1⋅V1=C2⋅V2=C3⋅V3
For our capacitors:
- C1=1μF
- C2=2μF
- C3=3μF
3. Express Voltages in Terms of Charge:
- From the charge equations, we can express V1, V2, and V3 in terms of Q:
V1=QC1=Q1=Q
V2=QC2=Q2
V3=QC3=Q3
4. Substitute into the Voltage Equation:
- Substitute V1, V2, and V3 into the total voltage equation:
Vtotal=V1+V2+V3=Q+Q2+Q3
5. Find a Common Denominator:
- The common denominator for 1, 2, and 3 is 6. Thus, we can rewrite the equation:
Vtotal=Q+3Q6+2Q6=Q+5Q6=11Q6
6. Set Equal to Total Voltage:
- We know from the problem that Vtotal=11V:
11Q6=11
7. Solve for Q:
- Multiply both sides by 6:
11Q=66
- Divide by 11:
Q=6μC
8. Calculate Voltage Across 1 μF Capacitor:
- Now, substitute Q back to find V1:
V1=QC1=6μC1μF=6V
Final Answer:
The potential difference across the plates of the 1 μF capacitor is 6 V.
- In a series connection of capacitors, the total voltage across the combination is equal to the sum of the voltages across each capacitor.
- Mathematically, this can be expressed as:
Vtotal=V1+V2+V3
where V1, V2, and V3 are the voltages across the 1 μF, 2 μF, and 3 μF capacitors respectively.
- In a series circuit, the charge (Q) on each capacitor is the same. The relationship between charge, capacitance, and voltage is given by:
Q=C⋅V
Therefore, we can write:
Q=C1⋅V1=C2⋅V2=C3⋅V3
For our capacitors:
- C1=1μF
- C2=2μF
- C3=3μF
- From the charge equations, we can express V1, V2, and V3 in terms of Q:
V1=QC1=Q1=Q
V2=QC2=Q2
V3=QC3=Q3
- Substitute V1, V2, and V3 into the total voltage equation:
Vtotal=V1+V2+V3=Q+Q2+Q3
- The common denominator for 1, 2, and 3 is 6. Thus, we can rewrite the equation:
Vtotal=Q+3Q6+2Q6=Q+5Q6=11Q6
- We know from the problem that Vtotal=11V:
11Q6=11
- Multiply both sides by 6:
11Q=66
- Divide by 11:
Q=6μC
- Now, substitute Q back to find V1:
V1=QC1=6μC1μF=6V
The potential difference across the plates of the 1 μF capacitor is 6 V.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Capacitor Circuits
Explore 52 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Problems Based On Mixed Concepts
Explore 44 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Capacitor With Dielectric
Explore 32 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section D - Chapter End Test
Explore 29 Videos
- ELECTROMAGNETIC INDUCTIONBook:A2ZChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
Three capacitors of capacities 8μF,8μFand4μF are connected in a series and a potential difference of 120 volt is maintained across the combination. Calculate the charge on capacitor of capacity 4μF.
View SolutionThree capacitors of capacities 8μF,8μFand4μF are connected in a series and a potential difference of 120 volt is maintained across the combination. Calculate the charge on capacitor of capacity 4μF.
View Solution
Knowledge Check
Three capacitors of capacities 12μF,6μFand4μF are connected in series and a potential difference of 20 V is applied to their combination. What is the cahrge on the capacitor of 4μF ?
A20μCB40μCC30μCD50μCIn the adjoning figure, the potential difference across the 4.5μF capacitor is
 A4 VB6 VC8 VD4.5 V
A4 VB6 VC8 VD4.5 VIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
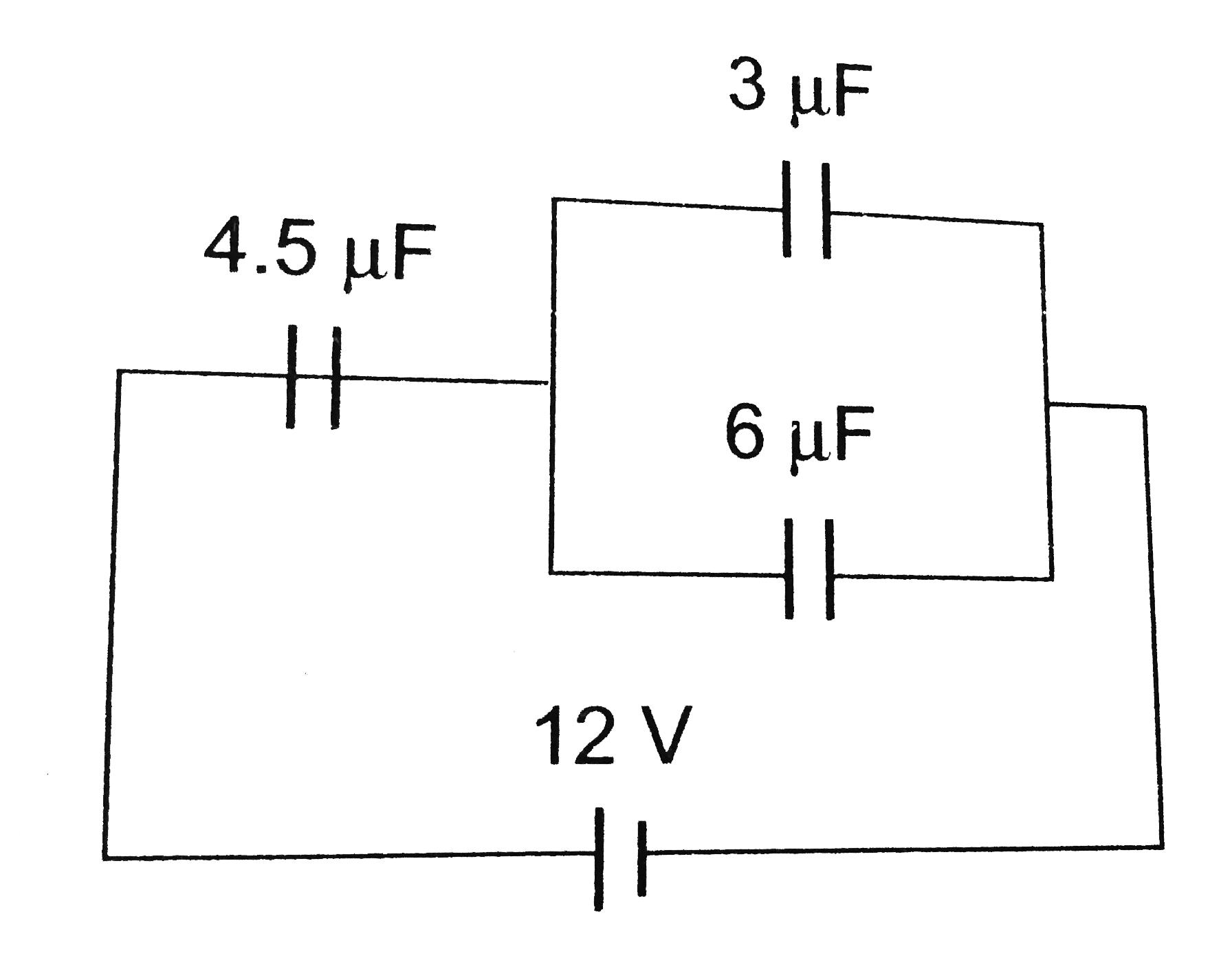 A83voltsB4 voltsC6 voltsD8 volts
A83voltsB4 voltsC6 voltsD8 volts
Three capacitors of capacitance 3μF,10μF and 15μF are connected in series to a voltage source of 100V. The charge on 15μF is
View SolutionTwo capacitors of 3μF and 6μF are connected in series and a potential difference of 900 V is applied across the combination. They are then disconnected and reconnected in parallel. The potential difference across the combination is
View SolutionThree capacitors of capacitacnce 1.0, 2.0 and 5.0μF are connected in series to a 10 V source. The potential difference across the 2.0μF capacitor is
View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
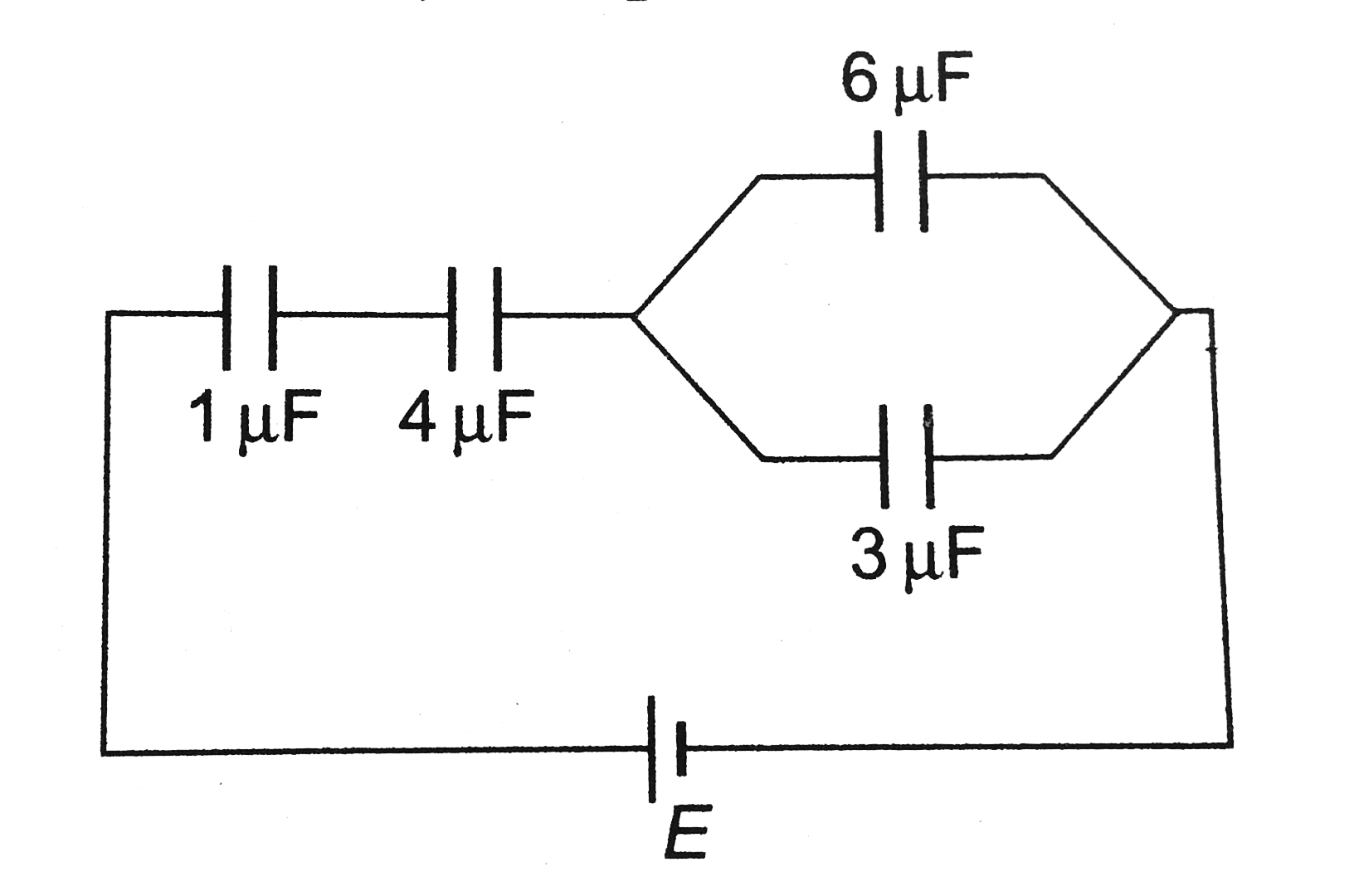
View SolutionTwo capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
View Solution