Two resistors are connected (a) in series (b) in parallel The equivalent resistance in the two cases are $9 o h m$ and $2 o h m$ respectively. Then the resistances of the component resistor are

A

$2 o h m$ and $7 o h m$

B

$3 o h m$ and $6 o h m$

C

$3 o h m$ and $9 o h m$

D

$5 o h m$ and $4 o h m$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem of finding the resistances of two resistors connected in series and parallel, we can follow these steps:
Step 1: Set Up the Equations
Let the two resistors be $R_{1}$ and $R_{2}$ .
1. When connected in series, the equivalent resistance $R_{s}$ is given by:
$R_{s} = R_{1} + R_{2}$
According to the problem, $R_{s} = 9 Ω$ . Therefore, we have:
$R_{1} + R_{2} = 9 (Equation 1)$
2. When connected in parallel, the equivalent resistance $R_{p}$ is given by:
$R_{p} = \frac{R_{1} \cdot R_{2}}{R_{1} + R_{2}}$
According to the problem, $R_{p} = 2 Ω$ . Therefore, we have:
$\frac{R_{1} \cdot R_{2}}{R_{1} + R_{2}} = 2 (Equation 2)$
Step 2: Substitute Equation 1 into Equation 2
From Equation 1, we can express $R_{1} \cdot R_{2}$ :
$R_{1} \cdot R_{2} = R_{p} \cdot (R_{1} + R_{2})$
Substituting $R_{p} = 2$ and $R_{1} + R_{2} = 9$ :
$R_{1} \cdot R_{2} = 2 \cdot 9 = 18 (Equation 3)$
Step 3: Solve the System of Equations
Now we have two equations:
1. $R_{1} + R_{2} = 9$ (Equation 1)
2. $R_{1} \cdot R_{2} = 18$ (Equation 3)
We can express $R_{1}$ in terms of $R_{2}$ using Equation 1:
$R_{1} = 9 - R_{2}$
Substituting this into Equation 3:
$(9 - R_{2}) \cdot R_{2} = 18$
Expanding this gives:
$9 R_{2} - R_{2}^{2} = 18$
Rearranging leads to:
$R_{2}^{2} - 9 R_{2} + 18 = 0$
Step 4: Solve the Quadratic Equation
We can solve the quadratic equation $R_{2}^{2} - 9 R_{2} + 18 = 0$ using the quadratic formula:
$R_{2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
Where $a = 1, b = - 9, c = 18$ :
$R_{2} = \frac{9 \pm \sqrt{(- 9)^{2} - 4 \cdot 1 \cdot 18}}{2 \cdot 1}$
Calculating the discriminant:
$R_{2} = \frac{9 \pm \sqrt{81 - 72}}{2} = \frac{9 \pm \sqrt{9}}{2} = \frac{9 \pm 3}{2}$
Thus, we have:
$R_{2} = \frac{12}{2} = 6 or R_{2} = \frac{6}{2} = 3$
Step 5: Find $R_{1}$
Using $R_{1} + R_{2} = 9$ :
1. If $R_{2} = 6$ , then $R_{1} = 9 - 6 = 3$ .
2. If $R_{2} = 3$ , then $R_{1} = 9 - 3 = 6$ .
Conclusion
The resistances of the two resistors are $R_{1} = 3 Ω$ and $R_{2} = 6 Ω$ (or vice versa).

Updated on:7/8/2024

|

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two resistors are connected (a) in series (b) in parallel. The equivalent resistance in the two cases are 9 ohm and respectively. Then the resistances of the component resistors are
A2 ohm and 7 ohm
B3 ohm and 6 ohm
C3 ohm and 9 ohm
D5 ohm and 4 ohm
Five resistors are connected as shown in the diagram. The equivalent resistance between $A$ and $B$ is

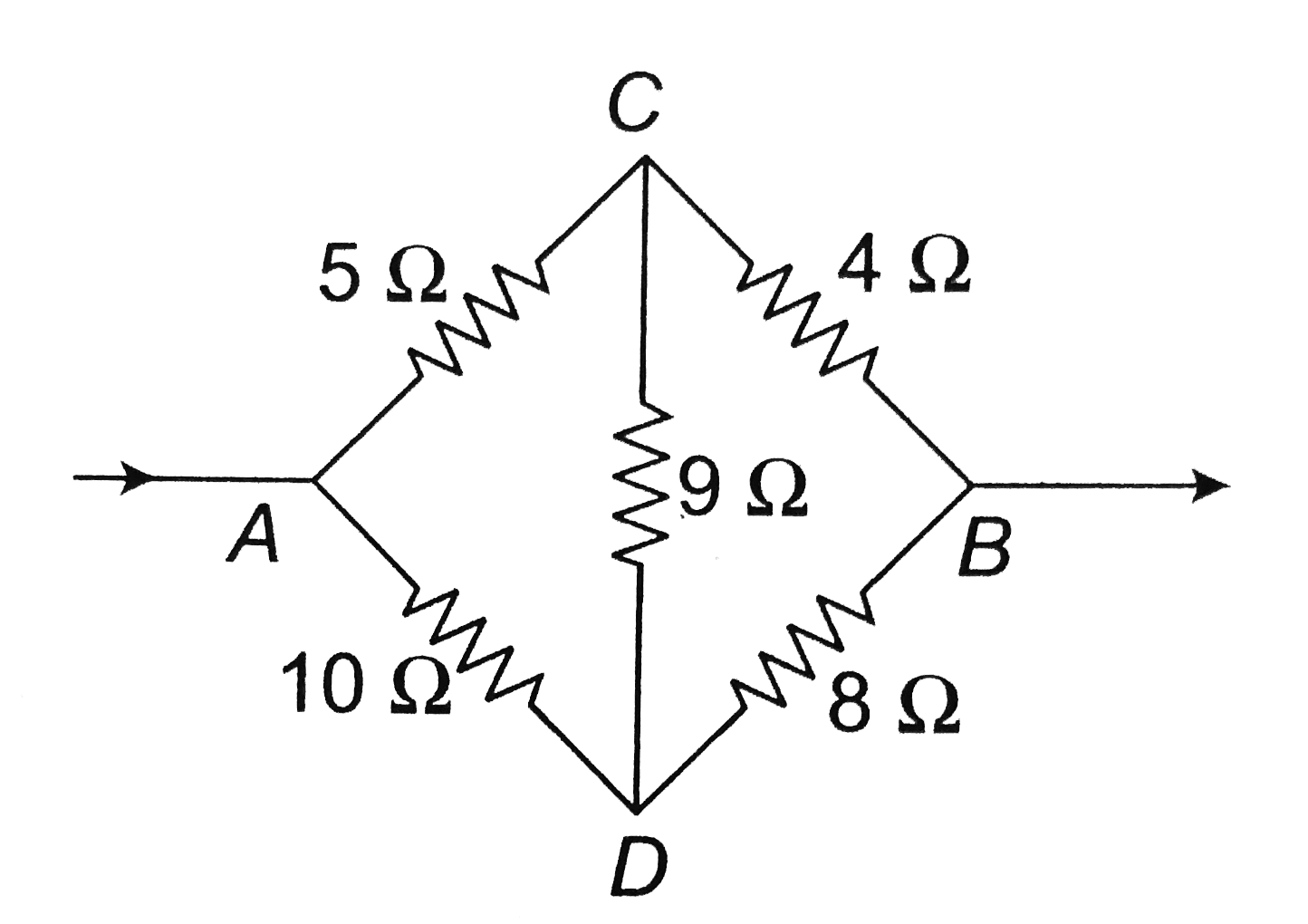A $6 o h m$
B $9 o h m$
C $12 o h m$
D $15 o h m$
A number of resistors are connected as shown in the figure. The equivalent resistance between A and B is

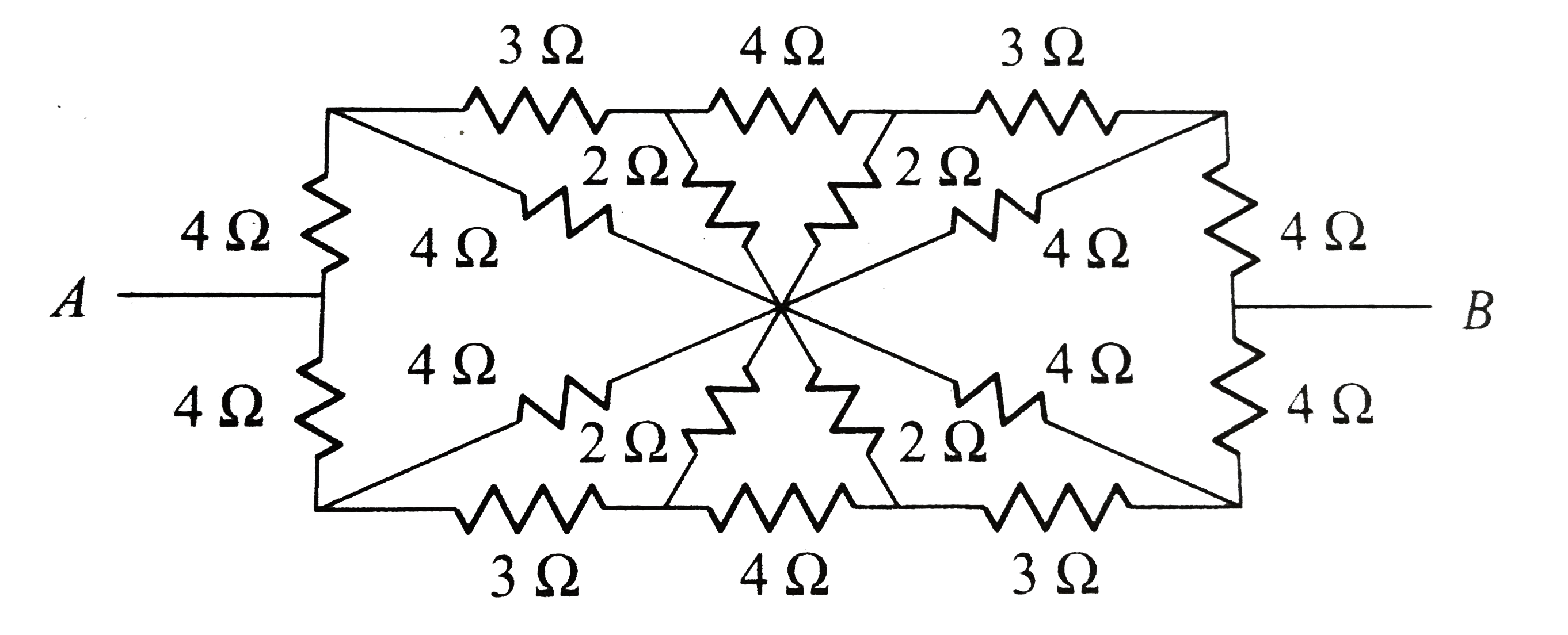A $6 Ω$
B $12 Ω$
C $9 Ω$
D $15 Ω$

A2Z-CURRENT ELECTRICITY-Combination And Resistivity

Home
Ask Doubt
Profile