If you are provided three resistance 2Ω,3Ω and 6Ω. How will you connect them so as to obtain the equivalent resistance of 4Ω
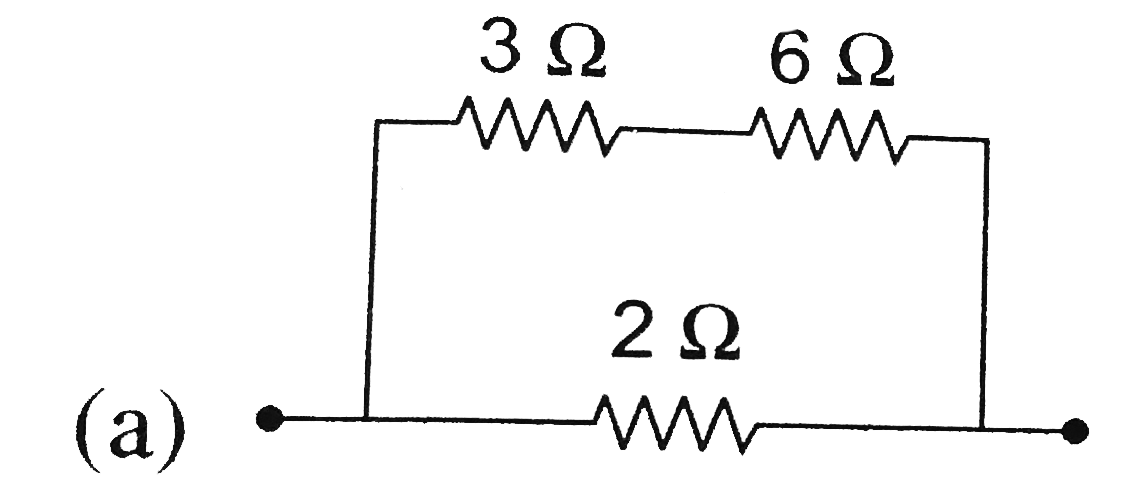

none
The correct Answer is:C
To solve the problem of obtaining an equivalent resistance of 4 ohms using the resistances of 2 ohms, 3 ohms, and 6 ohms, we can analyze the possible configurations of these resistors.
1. Understanding Series and Parallel Connections:
- In a series connection, the equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2+R3+…
- In a parallel connection, the equivalent resistance is given by:
1Req=1R1+1R2+1R3+…
2. Testing Different Configurations:
- We will check various combinations of the given resistances to find one that results in an equivalent resistance of 4 ohms.
3. Option A: Connect 3 ohms and 6 ohms in series, then in parallel with 2 ohms.
- Series combination:
Rseries=3+6=9Ω
- Now, calculate the equivalent resistance with 2 ohms in parallel:
1Req=19+12=2+918=1118
Req=1811≈1.64Ω(not equal to 4 ohms)
4. Option B: Connect 3 ohms and 2 ohms in series, then in parallel with 6 ohms.
- Series combination:
Rseries=3+2=5Ω
- Now, calculate the equivalent resistance with 6 ohms in parallel:
1Req=15+16=6+530=1130
Req=3011≈2.73Ω(not equal to 4 ohms)
5. Option C: Connect 3 ohms and 6 ohms in parallel, then add 2 ohms in series.
- Parallel combination:
1Rparallel=13+16=2+16=36=12
Rparallel=2Ω
- Now, add the 2 ohms in series:
Req=2+2=4Ω(this is equal to 4 ohms)
6. Conclusion:
- The configuration that gives an equivalent resistance of 4 ohms is to connect the 3-ohm and 6-ohm resistors in parallel and then connect the resulting 2-ohm resistance in series with the 2-ohm resistor.
Final Answer:
The equivalent resistance of 4 ohms can be obtained by connecting the 3-ohm and 6-ohm resistors in parallel, and then connecting the resulting 2-ohm resistance in series with the 2-ohm resistor.
- In a series connection, the equivalent resistance (R_eq) is the sum of the individual resistances:
Req=R1+R2+R3+…
- In a parallel connection, the equivalent resistance is given by:
1Req=1R1+1R2+1R3+…
- We will check various combinations of the given resistances to find one that results in an equivalent resistance of 4 ohms.
- Series combination:
Rseries=3+6=9Ω
- Now, calculate the equivalent resistance with 2 ohms in parallel:
1Req=19+12=2+918=1118
Req=1811≈1.64Ω(not equal to 4 ohms)
- Series combination:
Rseries=3+2=5Ω
- Now, calculate the equivalent resistance with 6 ohms in parallel:
1Req=15+16=6+530=1130
Req=3011≈2.73Ω(not equal to 4 ohms)
- Parallel combination:
1Rparallel=13+16=2+16=36=12
Rparallel=2Ω
- Now, add the 2 ohms in series:
Req=2+2=4Ω(this is equal to 4 ohms)
- The configuration that gives an equivalent resistance of 4 ohms is to connect the 3-ohm and 6-ohm resistors in parallel and then connect the resulting 2-ohm resistance in series with the 2-ohm resistor.
The equivalent resistance of 4 ohms can be obtained by connecting the 3-ohm and 6-ohm resistors in parallel, and then connecting the resulting 2-ohm resistance in series with the 2-ohm resistor.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Kircoff'S Laws And Simple Circuits
64 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - R-C Circuits
17 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section D - Chapter End Test
29 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
If you are provided three resistances 2Ω,3Ω and 6Ω. How will you connect then so as to obtain the equivalent resistance of 4Ω ?
A B
B C
C Dnone of these
Dnone of theseThe resistors of resistances 2Ω,4Ω and 8Ω are connected in parallel, then the equivalent resistance of the combination will be
A87ΩB78ΩC74ΩD49Ω
Which of the circuit has an equivalent resistance of 4Ω?
View SolutionYou have two metallic wires of resistances 6Ωand3Ω. How will you connect these wires to get the effective resistance of 2Ω?
View SolutionGiven the resistances of 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of
(i) 113Ω ?
(ii) 115Ω ?
View Solution(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
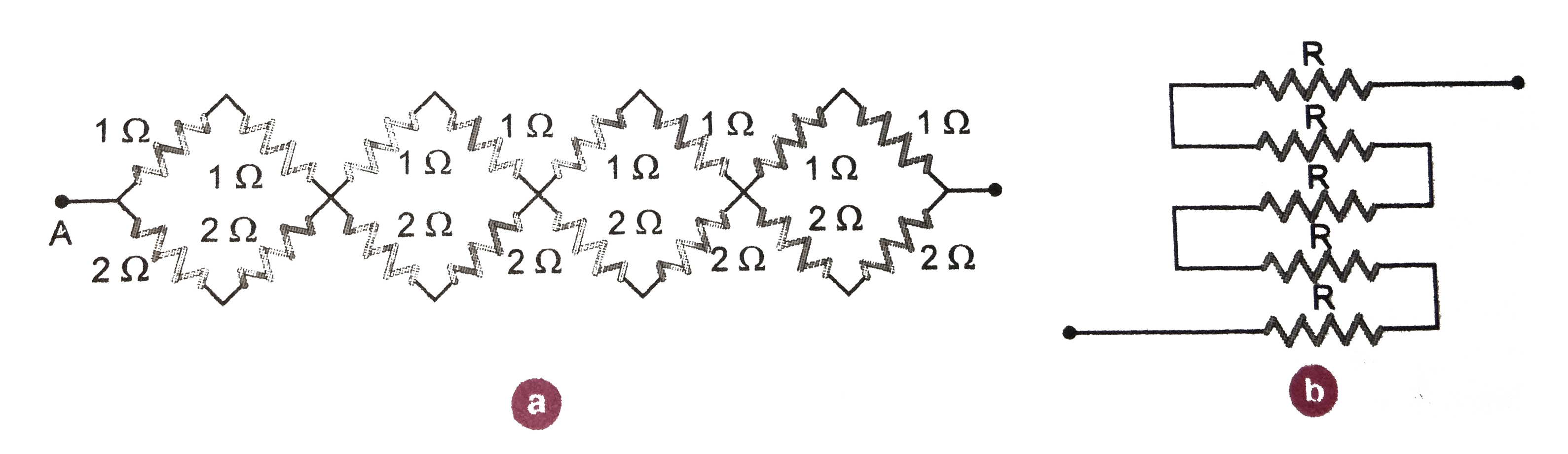
View SolutionThree resistors of 2Ω,3Ωand4Ω are connected in
(a) series
(b) parallel.
Find the equivalent resistance in each case.
View SolutionGiven the resistance of 1Ω,2Ω,3Ω, how will you combine them to get an e3quivalent resistance of :
113Ω (ii)115Ω (iii)6Ω 611Ω ?
View Solution
