Two resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
0.01
0.02
0.03
0.05
The correct Answer is:D
To solve the problem step-by-step, we will first find the actual potential difference across the 400 Ω resistor and then calculate the measured potential difference when the voltmeter is connected. Finally, we will find the error in the measurement.
Step 1: Calculate the Total Resistance in the Circuit
The two resistors, 400 Ω and 800 Ω, are connected in series. Therefore, the total resistance Rtotal is given by:
Rtotal=R1+R2=400Ω+800Ω=1200Ω
Hint: Remember that in a series circuit, the total resistance is simply the sum of the individual resistances.
Step 2: Calculate the Current in the Circuit
Using Ohm's Law, the current I flowing through the circuit can be calculated using the total voltage V and the total resistance Rtotal:
I=VRtotal=6V1200Ω=0.005A(or5mA)
Hint: Ohm's Law states that V=I×R. Rearranging it gives I=VR.
Step 3: Calculate the Actual Potential Difference Across the 400 Ω Resistor
The potential difference V400 across the 400 Ω resistor can be calculated using Ohm's Law:
V400=I×R1=0.005A×400Ω=2V
Hint: The voltage across a resistor in a series circuit can be found by multiplying the current through it by its resistance.
Step 4: Calculate the Equivalent Resistance with the Voltmeter
When the voltmeter (10,000 Ω) is connected across the 400 Ω resistor, it forms a parallel combination with the 400 Ω resistor. The equivalent resistance Req of the 400 Ω resistor and the voltmeter is given by:
1Req=1R1+1Rvoltmeter=1400+110000
Calculating this gives:
1Req=25+110000=2610000⟹Req=1000026≈384.6Ω
Hint: For resistors in parallel, the reciprocal of the total resistance is the sum of the reciprocals of the individual resistances.
Step 5: Calculate the New Total Resistance in the Circuit
Now, the total resistance in the circuit when the voltmeter is connected is:
Rtotal_new=Req+R2=384.6Ω+800Ω=1184.6Ω
Hint: When additional components are added in series, their resistances are added to the total resistance.
Step 6: Calculate the Current with the Voltmeter Connected
The current Inew in the circuit with the voltmeter connected is:
Inew=VRtotal_new=6V1184.6Ω≈0.00506A
Hint: Use the same formula for current as before, but with the new total resistance.
Step 7: Calculate the Measured Potential Difference Across the 400 Ω Resistor
Now, we can calculate the potential difference Vmeasured across the equivalent resistance:
Vmeasured=Inew×Req=0.00506A×384.6Ω≈1.95V
Hint: The measured voltage is calculated using the current through the equivalent resistance.
Step 8: Calculate the Error in Measurement
The error in measurement can be calculated as:
Error=Vactual−Vmeasured=2V−1.95V=0.05V
Hint: The error is simply the difference between the actual voltage and the measured voltage.
Conclusion
The error in the measurement of potential difference across the 400 Ω resistor is approximately 0.05 volts.
The two resistors, 400 Ω and 800 Ω, are connected in series. Therefore, the total resistance Rtotal is given by:
Rtotal=R1+R2=400Ω+800Ω=1200Ω
Using Ohm's Law, the current I flowing through the circuit can be calculated using the total voltage V and the total resistance Rtotal:
I=VRtotal=6V1200Ω=0.005A(or5mA)
The potential difference V400 across the 400 Ω resistor can be calculated using Ohm's Law:
V400=I×R1=0.005A×400Ω=2V
When the voltmeter (10,000 Ω) is connected across the 400 Ω resistor, it forms a parallel combination with the 400 Ω resistor. The equivalent resistance Req of the 400 Ω resistor and the voltmeter is given by:
1Req=1R1+1Rvoltmeter=1400+110000
Calculating this gives:
1Req=25+110000=2610000⟹Req=1000026≈384.6Ω
Now, the total resistance in the circuit when the voltmeter is connected is:
Rtotal_new=Req+R2=384.6Ω+800Ω=1184.6Ω
The current Inew in the circuit with the voltmeter connected is:
Inew=VRtotal_new=6V1184.6Ω≈0.00506A
Now, we can calculate the potential difference Vmeasured across the equivalent resistance:
Vmeasured=Inew×Req=0.00506A×384.6Ω≈1.95V
The error in measurement can be calculated as:
Error=Vactual−Vmeasured=2V−1.95V=0.05V
The error in the measurement of potential difference across the 400 Ω resistor is approximately 0.05 volts.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Potentiometer And Meter Bridge
45 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Heating Effect Of Current
40 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - R-C Circuits
17 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A voltmeter of resistance 600Ω is used to measure the potential drop across the 300Ω resistor. What will be the measured potential drop ?
View Solution(a) A cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance 100Ω. When a voltmeter is connected across the 100Ω resistance the ammeter reading is 0.04A. Find the voltage read by the voltmeter and its resistance. Had the voltmeter been an ideal one, what would have its reading ?
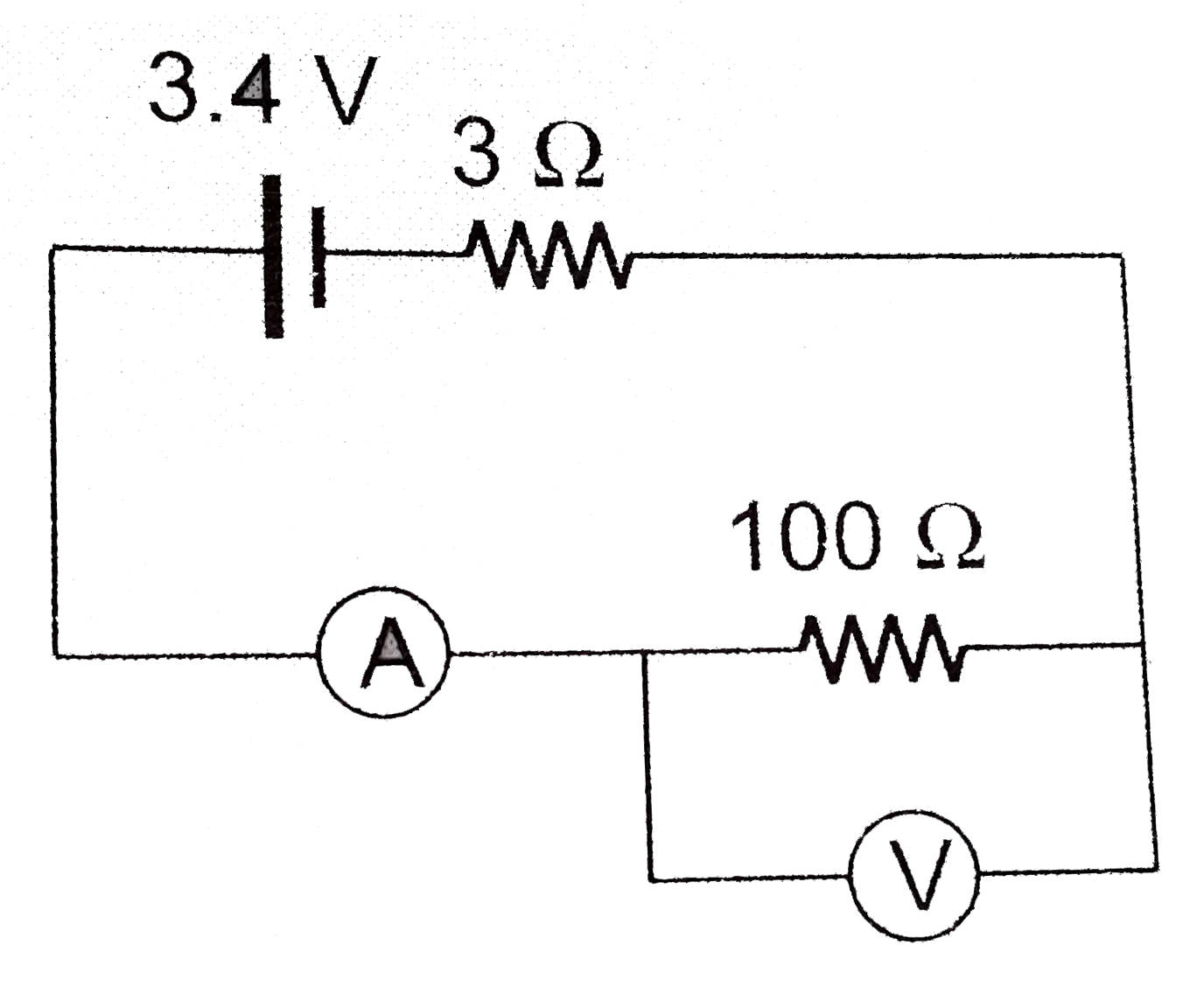
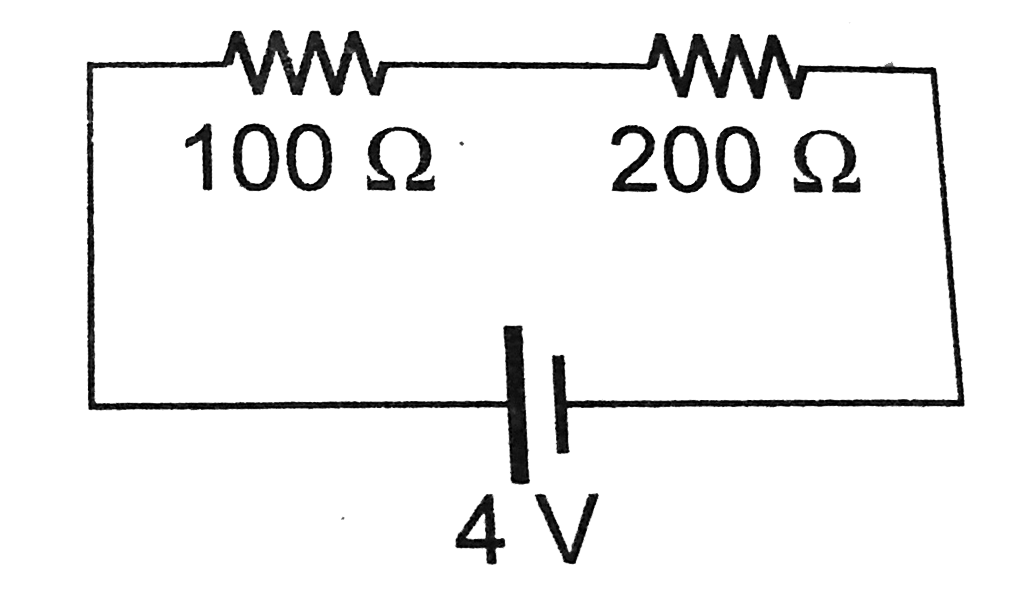
(b) Two resistances of 100Ω and 200Ω are connected in series with battery of emf 4V and negligible internal resistance. A voltmeter of resistance 200Ω is used to measure voltemeter of resistances separately. Calculate the voltmeter indicated.
( c) In the circuit shown, a voltmeter reads 30V when it is connected across the 400Ω resistance. Calculate what the same voltmeter will read when it is connected across the 300Ω resistance ?
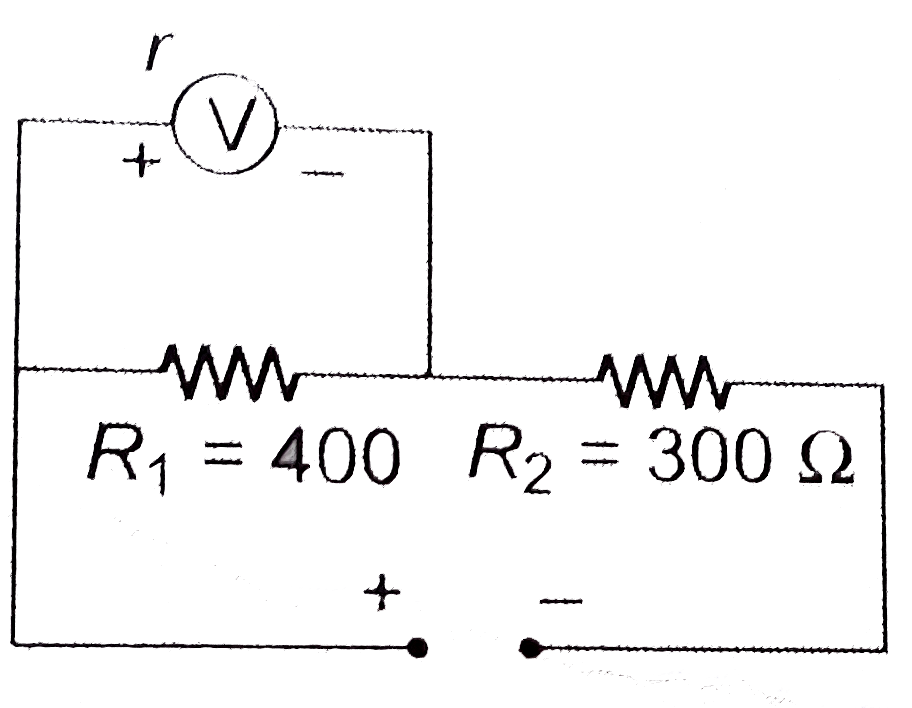
(d) An ammeter and a voltmeter are connected in series to a battery of emf E=6.0V. When a certain resistance is connected in parallel with the voltmeter. the reading of the ammeter is doubled. while voltmeter reading is reduced to half. Find the voltmeter reading after the connection of the resistance.
View Solution
Knowledge Check
Two resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
A0.05 VB0.5 VC0.75 VD5 VTwo resistors of 500Ω and 300Ω are connected in series with a battery of emf 20V.A voltmeter of resistance 500Ω is used to measure the p.d across the 500Ω resistor. The error in the measurement is.
A1.4 VB2.4 VC3.4 VD4.4 VA voltmeter of resistance 200Ω is used to measure p.d across resistances 100Ω and 200Ω.
 .AThe voltmeter reads 1V, when connected across 100ΩBThe voltmeter reads 2V, when connected across 200ΩCBoth (1) and (2)DNone
.AThe voltmeter reads 1V, when connected across 100ΩBThe voltmeter reads 2V, when connected across 200ΩCBoth (1) and (2)DNone
The battery of EMF 5V and internal resistance 20Ωis connected with a resistance R1=50Ω and a resistance . A voltmeter of resistance 1000Ω is used to measure the potential difference across R1 .What percentage error is made in the reading.
View SolutionA voltmeter resistance 500Ω is used to measure the emf of a cell of internal resistance 4Ω. The percentage error in the reading of the voltmeter will be
View SolutionTwo resistors 4Ω and 800Ω are connected in series with a 6V battery. The potential difference measured by voltmeter of 10kΩ across 400Ω resistor is
View SolutionA 10 m long wire ofresistance 20Ω is connected in series with battery of EMF 3V and negligible internal resistance and a resistance of 10Ω. The potential gradient along the wire is :
View SolutionA voltmeter resistance 500Ω is used to measure the emf of a cell of internal resistance 4Ω. The percentage error in the reading of the voltmeter will be
View Solution