Two straight long conductors and are perpendicular to each other and carry currents and . The magnitude of the magnetic induction at a point at a distance from the point in a direction perpendicular to the plane is :
The correct Answer is:C
To solve the problem of finding the magnitude of the magnetic induction at point P due to two perpendicular long conductors carrying currents I1 and I2, we can follow these steps:
Step 1: Understand the Configuration
We have two long straight conductors, AOB and COD, that are perpendicular to each other. The currents flowing through them are I1 in conductor AOB and I2 in conductor COD. The point P is located at a distance d from the intersection point O of the two conductors.
Step 2: Use Biot-Savart Law
According to the Biot-Savart Law, the magnetic field B due to a long straight conductor at a distance d from it is given by the formula:
B=μ0I2πd
where μ0 is the permeability of free space.
Step 3: Calculate Magnetic Fields Due to Each Conductor
1. Magnetic Field due to Conductor AOB:
BAOB=μ0I12πd
This magnetic field will be directed according to the right-hand rule.
2. Magnetic Field due to Conductor COD:
BCOD=μ0I22πd
This magnetic field will also be directed according to the right-hand rule.
Step 4: Determine the Directions of the Magnetic Fields
- The direction of BAOB will be out of the plane (let's assume it is in the positive x-direction).
- The direction of BCOD will be into the plane (let's assume it is in the negative y-direction).
Step 5: Calculate the Resultant Magnetic Field
Since the two magnetic fields are perpendicular to each other, we can use the Pythagorean theorem to find the magnitude of the resultant magnetic field Bnet:
Bnet=√B2AOB+B2COD
Substituting the expressions for BAOB and BCOD:
Bnet=√(μ0I12πd)2+(μ0I22πd)2
Step 6: Factor Out Common Terms
Factoring out the common terms:
Bnet=μ02πd√I21+I22
Final Answer
Thus, the magnitude of the magnetic induction at point P is:
Bnet=μ02πd√I21+I22
We have two long straight conductors, AOB and COD, that are perpendicular to each other. The currents flowing through them are I1 in conductor AOB and I2 in conductor COD. The point P is located at a distance d from the intersection point O of the two conductors.
According to the Biot-Savart Law, the magnetic field B due to a long straight conductor at a distance d from it is given by the formula:
B=μ0I2πd
where μ0 is the permeability of free space.
1. Magnetic Field due to Conductor AOB:
BAOB=μ0I12πd
This magnetic field will be directed according to the right-hand rule.
BCOD=μ0I22πd
This magnetic field will also be directed according to the right-hand rule.
- The direction of BAOB will be out of the plane (let's assume it is in the positive x-direction).
- The direction of BCOD will be into the plane (let's assume it is in the negative y-direction).
Since the two magnetic fields are perpendicular to each other, we can use the Pythagorean theorem to find the magnitude of the resultant magnetic field Bnet:
Bnet=√B2AOB+B2COD
Substituting the expressions for BAOB and BCOD:
Bnet=√(μ0I12πd)2+(μ0I22πd)2
Factoring out the common terms:
Bnet=μ02πd√I21+I22
Thus, the magnitude of the magnetic induction at point P is:
Bnet=μ02πd√I21+I22
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Problems Based On Mixed Concepts
32 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Dipole
32 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
The straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
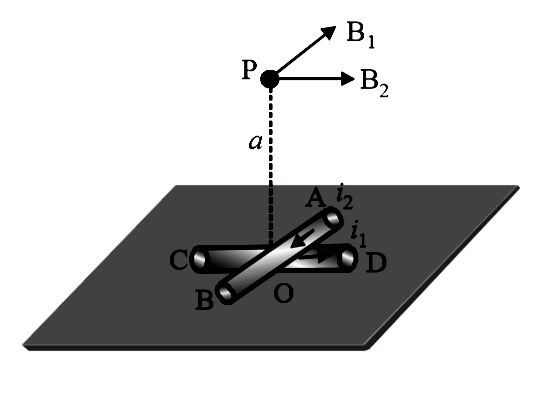
View SolutionTwo straight long conductors AOB and COD are perpendicular to each other and carry currents I1 and I2. Find the magnitude of magnetic field induction at a point P at a distance a from the point O in a direction perpendicular to the plane ABCD
View Solution
Knowledge Check
Two identical conducting wires AOBandCOD are placed at right angles to each other. The wire AOB carries an electric current I1andCOD carries a current I2. The magnetic field on a point lying at a distance d from O,∈adirectionperpendica––r→thepla≠ofthewiresAOB and COD, will be given by
Aμ02πd(I21+I22)Bμ02πI21+I22d)1/2Cμ02πd(I21+I22)1/2Dμ02πd(I1+I2)The magnitude of magnetic induction at a distance 4 cm due to straight conductor carrying a current of 10 A is
A5×10−6Wb/m2B5×10−5 N/AmC5×10−5 gaussD5×10−6 teslaThe magnetic induction at any point due to a long straight wire carrying a current is
AProportional to the distance from the wireBInversely proportional to the distance from wireCInversely proportional to the square of the distance from the wireDDoes not depend on distance
The magnitude of magnetic field at a point having perpendicular distance 50 mm from a long straight conducting wire carrying a current of 3A is
View SolutionTwo long mutually perpendicular conductors carrying currents I1 and I2 lie in one plane, Find the locus of points at which the magnetic induction is zero.
View SolutionTwo parallel straight long conducting wires, which are placed at a distance r from each other, are carrying equal currents I in opposite directions. The value of magnetic induction at a point situated at a point situated x from one wire in between the wires will be:
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
View SolutionTwo mutually perpendicular conductors carrying currents I1 and I2 lie in one plane. Locus of the point at which the magnetic induction is zero, is a:
View Solution
