Two mutually perpendicular conductors carrying currents I1 and I2 lie in one plane. Locus of the point at which the magnetic induction is zero, is a:
circle with centre as the point of intersection of the conductor
parabola with vertex as the point of intersection of the conductors
straight line passing through the point of intersection of the conductors
rectangular hyperbola
The correct Answer is:C
To solve the problem, we need to determine the locus of points where the magnetic induction (magnetic field) is zero due to two mutually perpendicular conductors carrying currents I1 and I2.
1. Understanding the Magnetic Field due to a Long Straight Conductor:
The magnetic field B at a distance r from a long straight conductor carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
2. Setting Up the Coordinate System:
Assume that the first conductor carrying current I1 is along the y-axis and the second conductor carrying current I2 is along the x-axis. Let the point P where we want to find the magnetic field be at coordinates (x,y).
3. Calculating the Magnetic Field at Point P:
- The magnetic field B1 due to the conductor along the y-axis at point P (distance y from the first conductor) is directed into the plane (using the right-hand rule):
B1=μ0I12πy^k
- The magnetic field B2 due to the conductor along the x-axis at point P (distance x from the second conductor) is directed out of the plane:
B2=−μ0I22πx^k
4. Setting the Net Magnetic Field to Zero:
For the net magnetic field B to be zero, we set the sum of the two magnetic fields equal to zero:
B1+B2=0
Substituting the expressions for B1 and B2:
μ0I12πy−μ0I22πx=0
5. Simplifying the Equation:
We can cancel μ02π from both sides:
I1y=I2x
Rearranging gives:
y=I1I2x
6. Identifying the Locus:
The equation y=I1I2x represents a straight line passing through the origin (0,0) with a slope of I1I2. This line is the locus of points where the magnetic induction is zero.
Conclusion:
The locus of the point at which the magnetic induction is zero is a straight line passing through the point of intersection of the conductors.
The magnetic field B at a distance r from a long straight conductor carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Assume that the first conductor carrying current I1 is along the y-axis and the second conductor carrying current I2 is along the x-axis. Let the point P where we want to find the magnetic field be at coordinates (x,y).
- The magnetic field B1 due to the conductor along the y-axis at point P (distance y from the first conductor) is directed into the plane (using the right-hand rule):
B1=μ0I12πy^k
- The magnetic field B2 due to the conductor along the x-axis at point P (distance x from the second conductor) is directed out of the plane:
B2=−μ0I22πx^k
For the net magnetic field B to be zero, we set the sum of the two magnetic fields equal to zero:
B1+B2=0
Substituting the expressions for B1 and B2:
μ0I12πy−μ0I22πx=0
We can cancel μ02π from both sides:
I1y=I2x
Rearranging gives:
y=I1I2x
The equation y=I1I2x represents a straight line passing through the origin (0,0) with a slope of I1I2. This line is the locus of points where the magnetic induction is zero.
The locus of the point at which the magnetic induction is zero is a straight line passing through the point of intersection of the conductors.
Similar Questions
Two long mutually perpendicular conductors carrying currents I1 and I2 lie in one plane, Find the locus of points at which the magnetic induction is zero.
 View Solution
View SolutionTwo infinitely long parallel cond uctors carrying currents are directed at right angles to the plane of the drawing. The magnetic induction at a point M that lies in the middle between the conductors is zero. To the right of this point, the magnetic induction vector points upward, at right angles to the x axis. Find the direction of the currents flowing in the conductors, the direction of the magnetic induction vector to the left of point M, the relationship between the currents, and the point on the x axis at which the magnetic induction is maximal. The distance between the conductors is a.
View Solution
Knowledge Check
- Question 1 - Select One
Two long straight conductors with corrents I1 and I2 are placed along X and Y axes. The equation of locus of points of zero magnetic induction is :
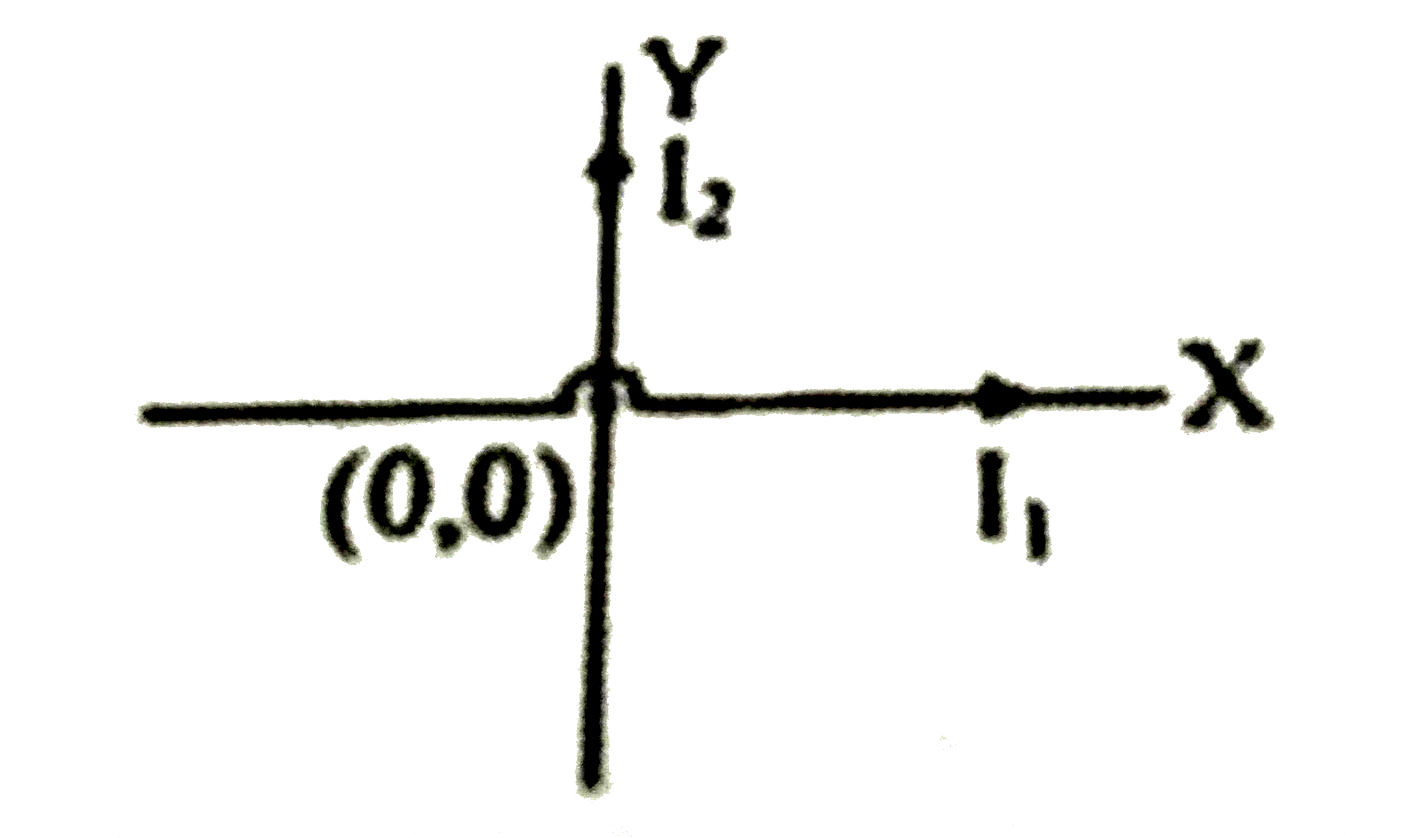 AY=XBY=I2XI2CY=I1I2XDY=XI1I2
AY=XBY=I2XI2CY=I1I2XDY=XI1I2 - Question 2 - Select One
Two mutually perpendicular insulated long conducting wires carrying equal currents I, intersect at origin. Then the resultant magnetic induction at point P (2m, 3m) will be-
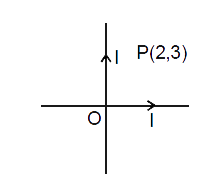 Aμ0I5aB5μ0I2πCμ0I12πD0
Aμ0I5aB5μ0I2πCμ0I12πD0 - Question 3 - Select One
Two straight long conductors AOB and COD are perpendicular to each other and carry currents I1 and I2. The magnitude of the magnetic induction at a point P at a distance d from the point o in a direction perpendicular to the plane ABCD is :
Aμ02πd(I1+I2)Bμ04πd(I1+I2)Cμ02πd√I22+I22Dμ02πd(I1I2I1+I2)
The straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
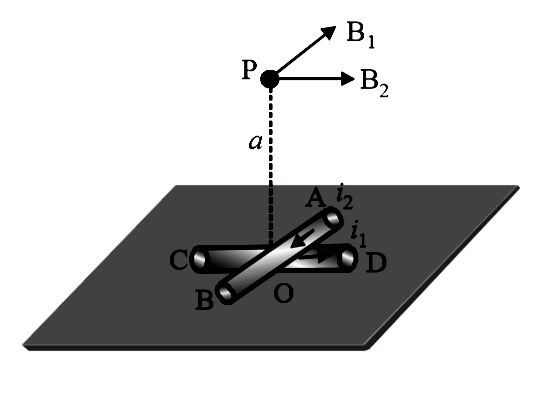 View Solution
View SolutionThe figure shows three straight current carrying conductors having current I1,I2 and I3 respectively. Calculate line integral of magnetic induction field →B along the closed path ABCDEFA
 View Solution
View SolutionA conductor is carrying a current i. the magnetic field intensity at a the point O which is the common centre of three arcs is
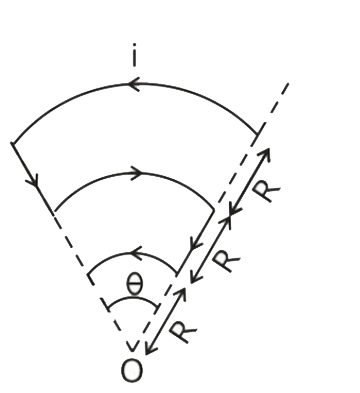 View Solution
View SolutionTwo long parallel conductors carry currents i1=3A and i2=3A both are directed into the plaane of paper. The magnitude of resultant magnetic field at point 'P', is
 View Solution
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
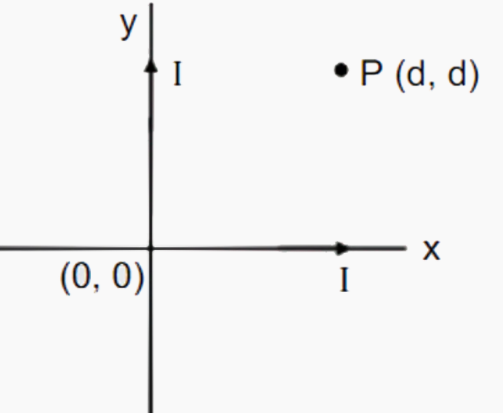 View Solution
View Solution

