A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is

$tan \frac{π}{n} t e s l a$

$\frac{μ_{0} I}{π R} [tan \frac{π}{n}] t e s l a$

$\frac{μ_{0} I}{2 π R} [tan \frac{π}{n}] t e s l a$

$\frac{μ_{0} I}{2 π R} [cos \frac{π}{n}] t e s l a$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is
A $\frac{μ_{0} I}{π R} (\frac{tan π}{n})$
B $\frac{μ_{0} I}{4 π R} \frac{tan π}{n}$
C $\frac{μ_{0} I}{2 π R} (\frac{tan π}{n})$
D $\frac{μ_{0} I}{2 π R} (\frac{cos π}{n})$
In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$ . Net magnetic field at centre will be

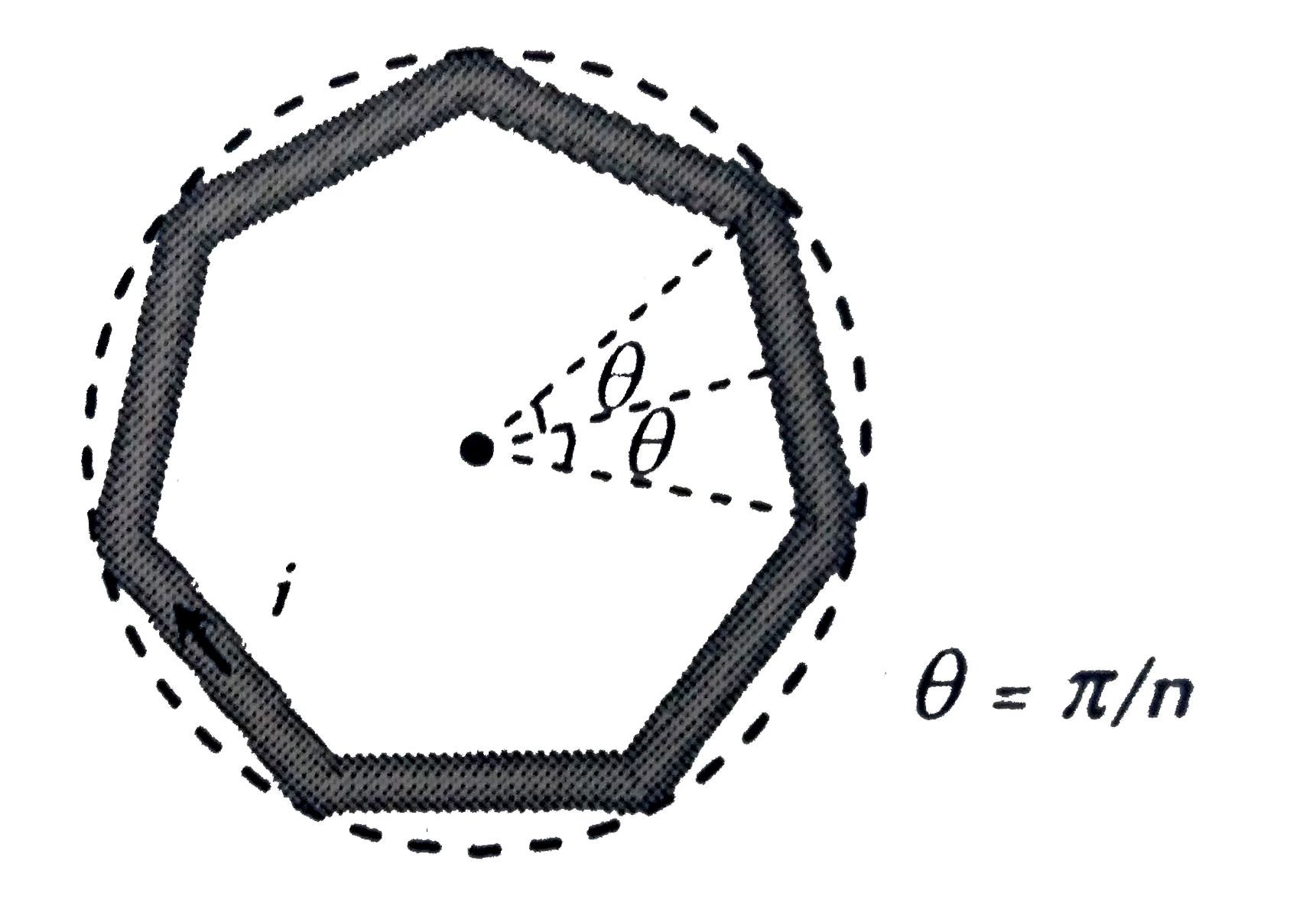A $\frac{μ_{0} i}{2 π a} tan \frac{π}{n}$
B $\frac{μ_{0} n i}{2 π a} tan \frac{π}{n}$
C $\frac{2}{π} \frac{n i}{a} μ_{0} tan \frac{π}{n}$
D $\frac{n i}{2 a} μ_{0} tan \frac{π}{n}$
A current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when $n \to \infty$ is (R is the radius of its circumcircle)
A $\frac{μ_{0} n i}{2 π R} tan \frac{π}{6}$
B $\frac{μ_{0} n i}{2 π R} tan \frac{π}{R}$
C $\frac{μ_{0} i}{2 R}$
Dzero