If a thin wire of length L is given the shape of a regular polygon of n sides and current I flows through it, what will be the net magnetic field at the centre of the polygon if n is infinity?
μ0ni2L
μ0ni2πL
μ0πiL
μ0nπiL
The correct Answer is:c
If the number of sides is kept infinite , it means that we can assume the polygon to be a circular loop. Let r be the radius of the circular loop, then
L=2πr⇒r=L/2π
Hence can write it as :
B=μ0i2L2π=μ0πiL
Therefore, option (c ) is correct.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)79videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)28videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )18videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
The limit of the interior angle of a regular polygon of n sides as n→∞ is
AπBπ3C3π2D2π3 - Question 2 - Select One
A wire shaped to a regular hexagon of side x carries a current I ampere. Calculate the strength of the magnetic field at the centre of the hexagon.
A√3μ0IπxB3μ0IπxCμ0I3πxDμ0I√3πx - Question 3 - Select One
A wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πL
Find the radius of the circumscribing circle of a regular polygon of n sides each of length is a.
View SolutionThe area of the circle and the area of a regular polygon of n sides and the perimeter equal to the circle are in the ratio of
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
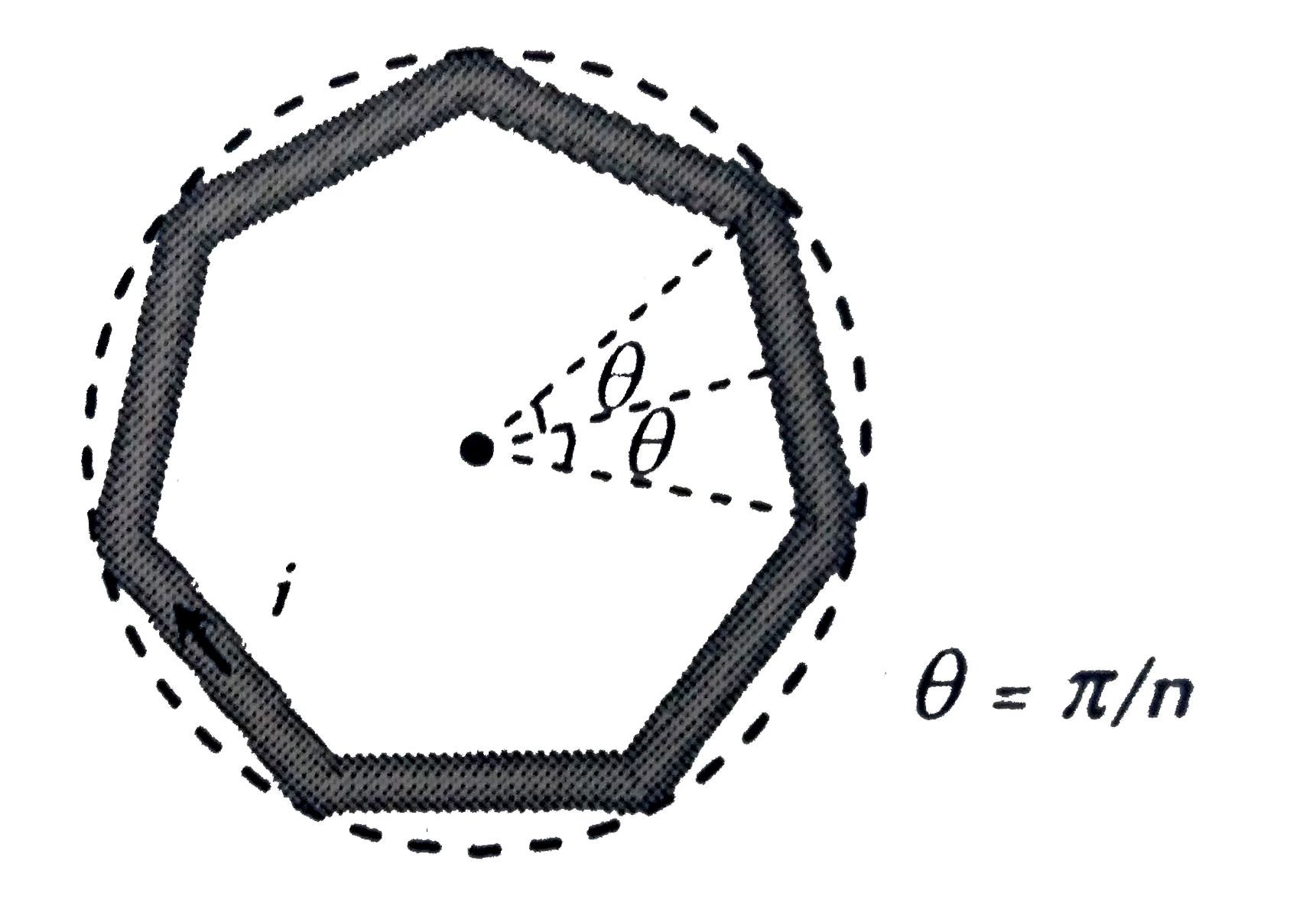 View Solution
View SolutionA conducting wire of length L is bent in the form of an equilateral triangle. If current I is made to pass through it, then calculate the magnetic field intensity at the centre of the triangle.
View SolutionThe area of the circle and the area of a regular polygon of n sides and the perimeter equal to the circle are in the ratio of
View Solution

