An otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
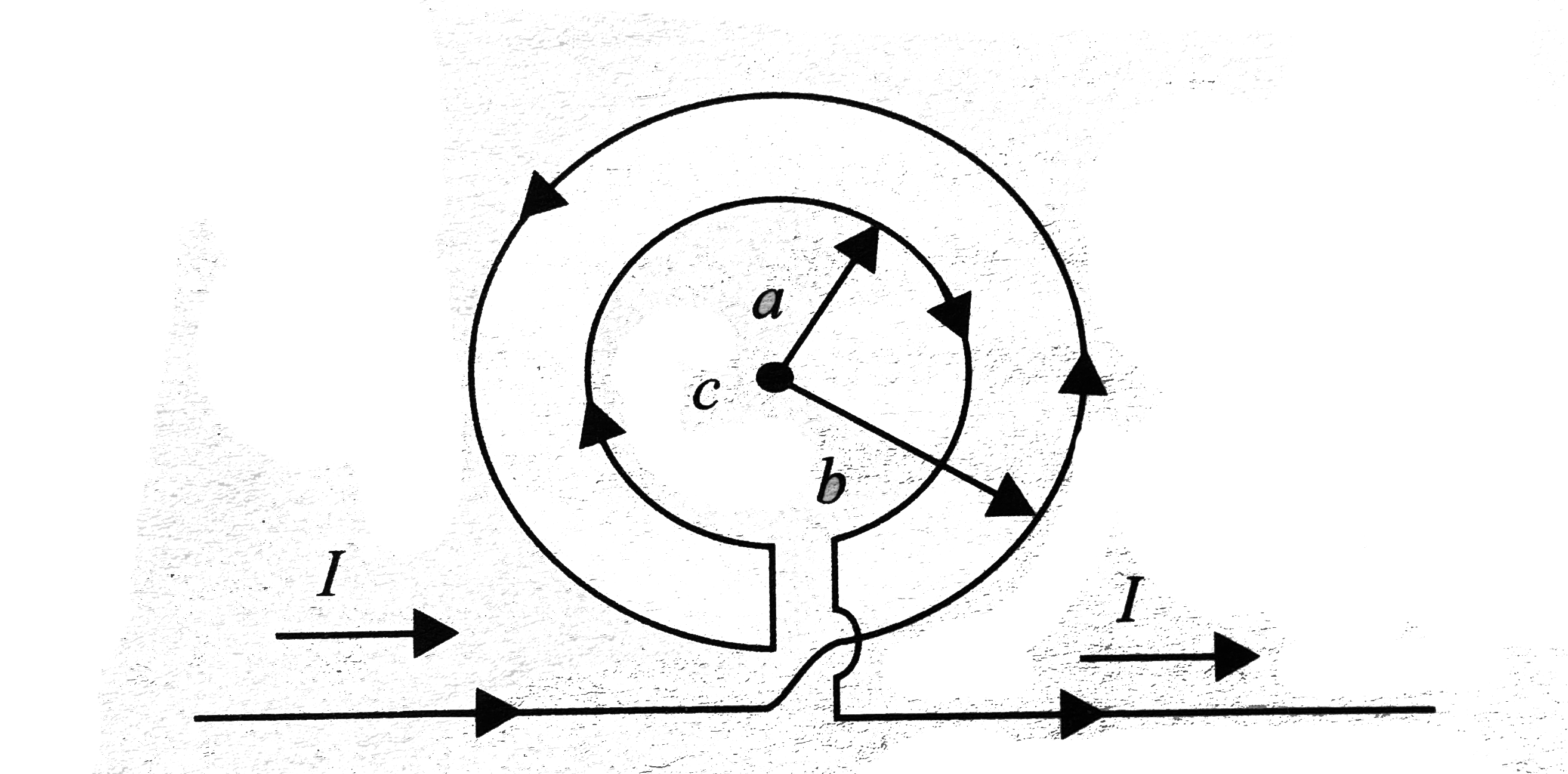
ab=π−1π
ab=ππ+1
ab=π−1π+1
ab=π+1π−1
The correct Answer is:B
Bcentre=0
μ0I4πb⊙+μ0I4πb⊙+μ0I2b⊙+μ0I2a⊗=0
μ0I2πb+μ0I2b−μ0I2a=0
12πb+12b=12a
ab=ππ−1
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Problems Based On Mixed Concepts32videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning31videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Current44videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE29videos
SEMICONDUCTOR ELECTRONICS
- BOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test29videos
WAVE OPTICS
Similar Questions
In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
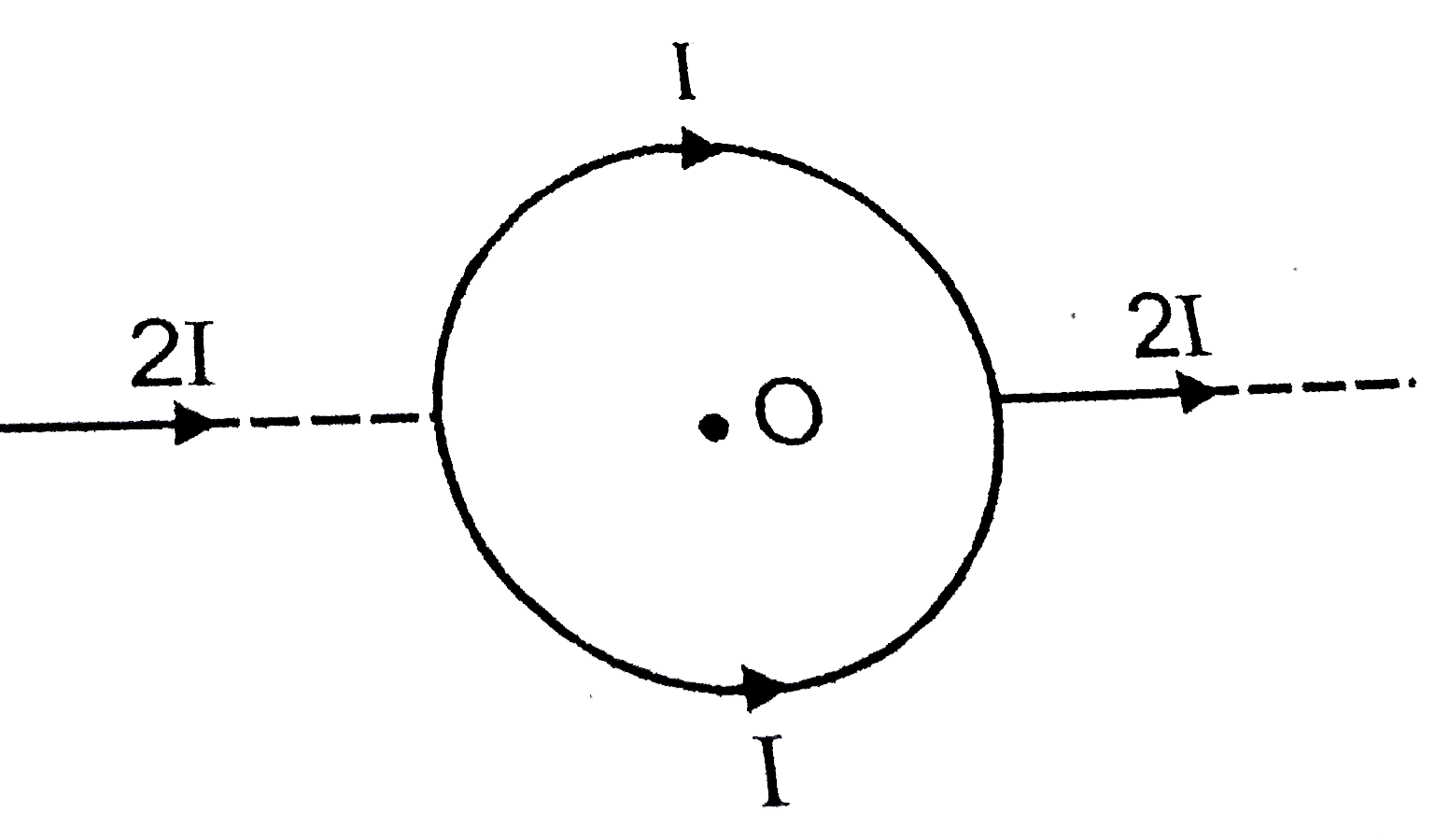
View SolutionAn infinite straigh conductor carrying current 2 I is split into a loop of radius r as shown in fig. the magnetic field at the centre of the coil is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
 AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2)
AzeroBμ0I4(1R1−1R2)Cμ0I4(1R2+1R1)Dμ0I2(1R1−1R2) - Question 2 - Select One or More
In a coaxial, straght cable, the central conductor and the outer conductor carry equal currents in opposite directions.The magnetic field is non-zero.
 Aoutside the cableBinside the inner conductor except axis of the conductorCall the point inside the outer conductor and outside inner conductorDonly on axis of conductors
Aoutside the cableBinside the inner conductor except axis of the conductorCall the point inside the outer conductor and outside inner conductorDonly on axis of conductors - Question 3 - Select One
A rectangular loop of conductor of length a and breadtlı b carrying current / is shown in the figure. The magnetic field at the centre o of the loop is
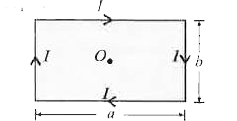 Aμ0(a+b)2π√a2+b2Bμ0Iab2π√a2+b2Cμ0(a+b)π√a2+b2D2μ0(a2+b2)πab
Aμ0(a+b)2π√a2+b2Bμ0Iab2π√a2+b2Cμ0(a+b)π√a2+b2D2μ0(a2+b2)πab
A long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.
 View Solution
View SolutionA square loop of side a carries a current I. The magnetic field at the center of the loop is
View SolutionTwo infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
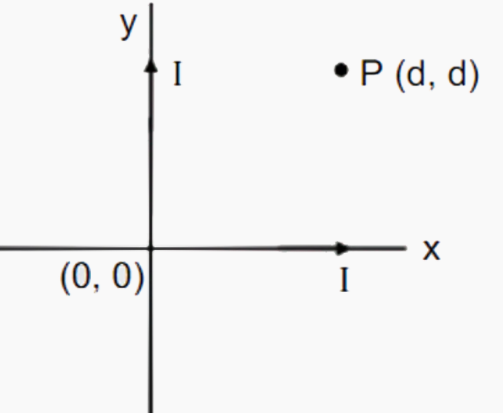 View Solution
View SolutionTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
View Solution

